Економічні науки/8.Математичні методи в економіці

Шевченко Г.В.

Київський національний економічний університет ім.В.Гетьмана. Україна

Моделювання розміщення рекламних оголошень на різних носіях реклами

На сьогоднішній день проблема оптимального розміщення реклами з максимальним охопленням цільової аудиторії є актуальною для підприємств. Представлено модель, головне завдання якої полягає в тому, щоб максимізувати досяжність рекламних оголошень до бажаної групи людей в межах допустимого бюджету без порушення кількості рекламних цілей. В якості носіїв розглядались різні профільні журнали:«Автоцентр», «Нові автомобілі», «Комерційні автомобілі» та «Автобазар» (в подальшому Журнал 1, Журнал 2, Журнал 3 і Журнал 4, відповідно) та встановлюються критерії щодо цільової аудиторії: статок , посада; вік. Був вибраний фіксований розмір рекламного оголошення, наприклад, 213 х 137мм. Необхідно знайти об’єм реклами, яку потрібно розмістити в різних ЗМІ, в межах допустимого бюджету, щоб максимізувати бажану досяжність до цільової аудиторії.

Нехай, - рекламні витрати на одне рекламне оголошення в кожному з журналів, r – кількість можливих позицій, приймає значення 1, або 2 , де 1 – відповідає рекламі на обкладинці, а 2- на будь-якій іншій сторінці. Значення тиражів: k₁, k₂, k₃, k₄. Нехай - змінні прийняття рішення, які відповідають кількості рекламних оголошень в різних журналах відповідно. Якщо a₁, а₂, а₃, а₄ – досяжність до цільової аудиторії для одного рекламного оголошення в журналах 1 – 4, тоді :

; ;

; .

В Таблиці 1 наведені тиражі обраних видань, а в Таблиці 2 приведена вартість рекламних оголошень для різних видань.

Таблиця 1

Тиражі обраних видань

Журнал1	Журнал2	Журнал3	Журнал4
k1 =200 000	k2 =200 000	k3 =20 000	k4 = 180 000

Таблиця 2.

Вартість рекламного оголошення

Місце розташування	Журнал 1	Журнал 2	Журнал 3	Журнал 4
Обкладинка	С11=34.600	С12=20.900	С13=4900	С14=18.000
Інша сторінка	С21=24.000	С22=9.400	С23=3.500	С24=14.900

,33;

Необхідно зауважити, що рекламний бюджет фіксований. Позначимо його М =125.000. Таким чином, сформулюємо задачу:

Максимізувати цільову функцію:

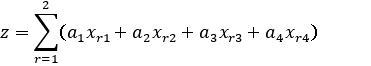
за умови:

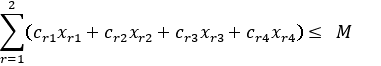
, r = 1,2; k = 1,2,3,4,

де t_ri` (i = 1…4) – мінімальна кількість рекламних оголошень в різних місцях для журналів 1-4; u_ri`` (i = 1…4) – максимальна кількість рекламних оголошень в різних місцях для журналів 1 – 4.

З урахуванням наведених вище числових даних, задачу можна записати наступним чином:

Максимізувати:

Z = 162600x₁₁ + 162600x₁₂ + 16632x₁₃ + 145818x₁₄ + 162600x₂₁ + 162600x₂₂ + 16632x₂₃ + 145818x₂₄

за умови:

34600x₁₁ + 20900x₁₂ + 4900x₁₃ + 18000x₁₄ + 24000x₂₁ + 9400x₂₂ + 3500x₂₃ + 14900x₂₄ ≤ 125 000;

X₁₁ ≤2, х₁₁ ≥1, x₁₂≥0, x₁₂≤3, x₁₃ ≥ 2, x₁₃ ≤ 4, x₁₄ ≥ 0, x₁₄ ≤ 2, x₂₁ ≥ 0, x₂₁ ≤ 2, x₂₂≥3, x₂₂ ≤ 6, x₂₃ ≥ 2, x₂₃ ≤ 7, x₂₄ ≤ 3, x₂₄ ≥ 1.

За допомогою симплекс-метода отримано наступний оптимальний розв’язок: Z = 1373050; x₁₁ = 1, x₁₂ = 0, x₁₃ = 2, x₁₄ = 0, x₂₁ = 0, x₂₂ = 6, x₂₃ = 2, x₂₄ = 2.

Таким чином, слід розмістити одне рекламне оголошення на обкладинці в журналі «Автоцентр», шість рекламних оголошень на внутрішніх сторінках каталогу «Нові автомобілі», по два рекламних оголошення на обкладинці та на внутрішніх сторінках журналу «Комерційнй автомобілі» і два рекламних оголошення в каталозі «Автобазар».

Отже, модель була сформульована таким чином, щоб реклама досягала саме тієї групи, для якої призначалась дана продукція, а не тієї групи, яка не є потенційним споживачем. Для ілюстрації методології розв’язання був розглянутий випадок представництва автомобільного заводу, що випускає вантажні автомобілі, зацікавленого в розміщенні реклами своєї продукції в засобах масової інформації.

Література:

1. Вітлінський В.В. / Моделювання економіки: навч. посіб. / В.В Вітлінський. – К.: КНЕУ, 2003. – 408 с.

2. В.В.Вітлінський, П.І.Верченко, А.В.Сігал, Я.С.Наконечний. Економічний ризик: ігрові моделі. Навч. пос. За ред. проф. В.В.Вітлінського. К.: КНЕУ, 2002 .- С.447.

3. Kwak, N.K., Lee, Chang Won, Kim, Ji Hee, An MCDM model for media selection in the dual consumer/industrial market. European Journal of

Operational Research 166, 2005. - р255–265.