Мурзабекова М.А.
Магистр МКТУ
им. А.Ясави, Казахстан
КРАЕВАЯ ЗАДАЧА
ДЛЯ СИСТЕМ ИНТЕГРО-ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПАРАМЕТРОМ
На отрезке ![]() рассматривается двухточечная краевая задача для системы
интегро-дифференциальных уравнений с параметром
рассматривается двухточечная краевая задача для системы
интегро-дифференциальных уравнений с параметром
![]()
![]() (1)
(1)
![]() , (2)
, (2)
где ![]() -
матрица
-
матрица ![]() ,
,
![]() и
и ![]() -мерная вектор-функция
-мерная вектор-функция ![]() непрерывны на
непрерывны на ![]() ,
матрица
,
матрица ![]() непрерывна соответственно на
непрерывна соответственно на ![]() .
.
Требуется найти пару ![]() ,
которая
удовлетворяет системе интегро-дифференциальных уравнений с параметром (1) и
граничным условиям (2).
,
которая
удовлетворяет системе интегро-дифференциальных уравнений с параметром (1) и
граничным условиям (2).
В настоящей работе краевая задача для
интегро-дифференциальных уравнений с параметром (1), (2) исследуется методом параметризации [1,2].
Берем шаг ![]() , который
, который ![]() раз укладывается на отрезке
раз укладывается на отрезке ![]() и по нему произведем разбиение
и по нему произведем разбиение ![]() .
.
Сужение функции ![]() на
на ![]() ый интервал
ый интервал ![]() обозначим через
обозначим через ![]() , т.е.
, т.е. ![]() - система вектор - функций, определенная и совпадающая с
- система вектор - функций, определенная и совпадающая с ![]() на
на
![]() . Тогда исходная двухточечная краевая задача для систем
интегро-дифференциальных уравнений с параметром сведется к эквивалентной
многоточечной краевой задаче
. Тогда исходная двухточечная краевая задача для систем
интегро-дифференциальных уравнений с параметром сведется к эквивалентной
многоточечной краевой задаче
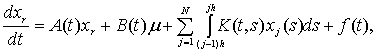
![]() (3)
(3)
![]() (4)
(4)
![]()
![]() . (5)
. (5)
Здесь
(5) - условия склеивания решения во внутренних точках разбиения ![]()
![]() .
.
Введем
обозначения ![]() =
= ![]() ,
, ![]() и на каждом интервале
и на каждом интервале ![]() произведем замену
произведем замену ![]() ,
, ![]() . Тогда задача (3) - (5) сведется к эквивалентной многоточечной
краевой задаче
. Тогда задача (3) - (5) сведется к эквивалентной многоточечной
краевой задаче
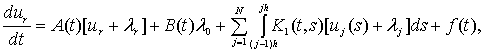 (6)
(6)
![]()
![]()
![]() (7)
(7)
![]() (8)
(8)
![]()
![]() . (9)
. (9)
Появление начальных условий ![]()
![]() позволяют при фиксированных значениях
позволяют при фиксированных значениях ![]() определить функции
определить функции ![]()
![]() из систем интегральных
уравнений
из систем интегральных
уравнений
![]()
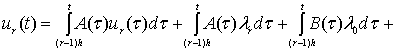
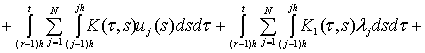
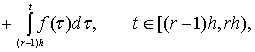
![]() (10)
(10)
Из (10)
определив ![]()
![]()
![]() , подставляя соответствующие им выражения в условия (8), (9)
и умножая обе части (8) на
, подставляя соответствующие им выражения в условия (8), (9)
и умножая обе части (8) на ![]() , получим систему линейных уравнений относительно неизвестных
параметров
, получим систему линейных уравнений относительно неизвестных
параметров ![]() ,
, ![]()
![]() (11)
(11)
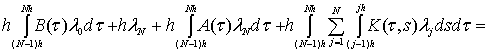
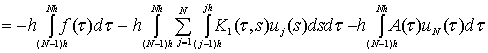 , (12)
, (12)
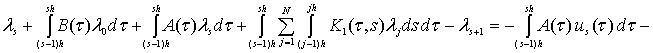
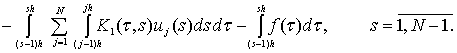 (13)
(13)
Матрицу
размерности ![]() , соответствующую левой части систем линейных уравнений (11),
(12) и (13) обозначим через
, соответствующую левой части систем линейных уравнений (11),
(12) и (13) обозначим через ![]() . Тогда система линейных уравнений (11), (12) и (13)
записывается в виде
. Тогда система линейных уравнений (11), (12) и (13)
записывается в виде
![]()
![]()
![]() , (14)
, (14)
где
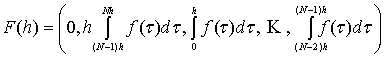 ,
,
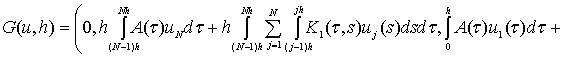
![]()

![]()
![]()
Таким
образом, для нахождения неизвестных пар ![]() , решения задачи (6) - (9), имеем замкнутую систему уравнений
(10), (14). Решение многоточечной краевой задачи (6) - (9) найдем как предел последовательности пар
, решения задачи (6) - (9), имеем замкнутую систему уравнений
(10), (14). Решение многоточечной краевой задачи (6) - (9) найдем как предел последовательности пар ![]() ,
, ![]() 0,1,2, …, определяемой по следующему алгоритму:
0,1,2, …, определяемой по следующему алгоритму:
Шаг 0.
а) Предполагая, что матрица ![]() обратима, из
уравнения
обратима, из
уравнения ![]() определим начальное
приближение по параметру
определим начальное
приближение по параметру ![]() :
: ![]()
б) Подставляя
найденные ![]()
![]() в правую часть
системы интегро-дифференциальных уравнений (6) и решая специальную задачу Коши с условиями (7) находим
в правую часть
системы интегро-дифференциальных уравнений (6) и решая специальную задачу Коши с условиями (7) находим ![]()
Шаг 1. а) Подставляя найденные ![]() ,
, ![]() , в правую часть (14)
из уравнения
, в правую часть (14)
из уравнения ![]() определим
определим ![]() .
.
б) Подставляя
найденные ![]()
![]() в правую часть
системы интегро-дифференциальных уравнений (6) и решая специальную задачу Коши с условиями (7) находим
в правую часть
системы интегро-дифференциальных уравнений (6) и решая специальную задачу Коши с условиями (7) находим ![]() И т.д.
И т.д.
Продолжая процесс, на ![]() -шаге алгоритма находим систему пар
-шаге алгоритма находим систему пар ![]() ,
, ![]() 0,1,2, ….
0,1,2, ….
Литературы
1.
Джумабаев Д.С.
Признаки однозначной разрешимости
линейной краевой задачи для систем дифференциальных уравнений //Журнал вычисл. матем. и матем. физ. 1989. Т. 29. № 1. С. 50-66.
2.
Джумабаев Д.С.
Критерий однозначной разрешимости
линейной краевой задачи для систем интегро-дифференциальных уравнений //Математический журнал 2008. Т. 8. № 2. С. 44-48.