Пилипюк
Т.М.
Кам’янець-Подільський
національний університет імені Івана Огієнка
ІНТЕГРАЛЬНЕ ЗОБРАЖЕННЯ
РОЗВ’ЯЗКУ МІШАНОЇ ЗАДАЧІ ДЛЯ СИСТЕМИ ЕВОЛЮЦІЙНИХ РІВНЯНЬ ПАРАБОЛІЧНОГО ТИПУ,
ЗМОДЕЛЬОВАНИХ МЕТОДОМ ГІБРИДНОГО ДИФЕРЕНЦІАЛЬНОГО ОПЕРАТОРА БЕССЕЛЯ-ЕЙЛЕРА-(КОНТОРОВИЧА-ЛЄБЄДЄВА)
НА КУСКОВО-ОДНОРІДНІЙ ПОЛЯРНІЙ ОСІ З М’ЯКИМИ МЕЖАМИ
Знайдемо інтегральне зображення
обмеженого в області ![]() аналітичного
розв'язку сепаратної системи рівнянь теплопровідності параболічного типу [1]
аналітичного
розв'язку сепаратної системи рівнянь теплопровідності параболічного типу [1]
![]() ,
, ![]()
![]()
![]() (1)
(1)
![]()
![]()
за початковими умовами
![]()
![]()
![]() ,
, ![]()
![]() (2)
(2)
та умовами спряження
![]() (3)
(3)
У
системі (1) беруть участь диференціальні оператори Бесселя ![]() [2], Ейлера
[2], Ейлера ![]() [6] та Конторовича-Лєбєдєва
[6] та Конторовича-Лєбєдєва ![]() [3];
[3]; ![]()
![]()
![]()
![]()
![]()
У
рівностях (3) беруть участь диференціальні оператори
![]()
Умови на коефіцієнти: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Для розв’язання мішаної задачі (1)-(3)
залучимо інтегральне перетворення Лапласа стосовно ![]() [4] в припущенні, що задані функції
[4] в припущенні, що задані функції ![]() та шукана вектор-функція
та шукана вектор-функція
![]()
![]() є
оригіналом за Лапласом.
є
оригіналом за Лапласом.
У зображенні за Лапласом задачі
(1)-(3) відповідає крайова задача: побудувати обмежений на множині ![]() розв'язок сепаратної
системи диференціальних рівнянь Бесселя, Ейлера та Конторовича-Лєбєдєва для
модифікованих функцій
розв'язок сепаратної
системи диференціальних рівнянь Бесселя, Ейлера та Конторовича-Лєбєдєва для
модифікованих функцій
![]()
![]() (4)
(4)
![]() .
.
за умовами спряження
![]() (5)
(5)
У рівностях (4), (5) прийняті
позначення: ![]()
![]()
![]()
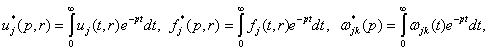
![]() де
де ![]() - абсциса збіжності
інтеграла Лапласа,
- абсциса збіжності
інтеграла Лапласа, ![]()
Можна
вважати, що ![]()
![]() В інакшому випадку
перейдемо до нових початкових даних:
В інакшому випадку
перейдемо до нових початкових даних:
![]()
![]()
Знайдемо величини ![]() та
та ![]() із алгебраїчної
системи:
із алгебраїчної
системи:
![]()
![]() (6)
(6)
Ми одержали алгебраїчну неоднорідну лінійну систему
чотирьох рівнянь відносно чотирьох невідомих величин ![]() При виконанні умов на
коефіцієнти алгебраїчна система (6) має єдиний розв'язок, який можна одержати
за правилами Крамера [5]:
При виконанні умов на
коефіцієнти алгебраїчна система (6) має єдиний розв'язок, який можна одержати
за правилами Крамера [5]:
![]()
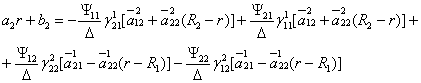 , (7)
, (7)
![]()
У
рівностях (7) беруть участь величини:
![]()
![]()
![]()
![]()
![]()
Зауважимо,
що числа ![]() з'являються у
результаті м'якості ліній
з'являються у
результаті м'якості ліній ![]() спряження по
відношенню до відбиття теплових хвиль, які виникають при поширенні початкової
температури.
спряження по
відношенню до відбиття теплових хвиль, які виникають при поширенні початкової
температури.
Нагадаємо,
що фундаментальну систему розв'язків для диференціального рівняння Бесселя ![]() складають
модифіковані функції Бесселя першого роду
складають
модифіковані функції Бесселя першого роду ![]() та другого роду
та другого роду ![]() [2]; фундаментальну
систему розв'язків для диференціального рівняння Ейлера
[2]; фундаментальну
систему розв'язків для диференціального рівняння Ейлера ![]() складають функції
складають функції ![]() та
та ![]() [6]; фундаментальну систему розв'язків для диференціального
рівняння Конторовича-Лєбєдєва
[6]; фундаментальну систему розв'язків для диференціального
рівняння Конторовича-Лєбєдєва ![]() складають
модифіковані функції Бесселя
складають
модифіковані функції Бесселя ![]() та
та ![]() [3].
[3].
Наявність
фундаментальної системи розв'язків дозволяє побудувати розв'язок крайової
задачі (4), (5) методом функцій Коші [6,7]:
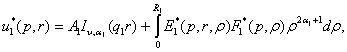
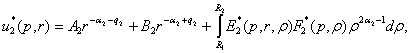 (8)
(8)

У рівностях (8) ![]() - функції Коші [6,7]:
- функції Коші [6,7]:
![]()
![]()
![]() (9)
(9)
Припустимо, що функція Коші
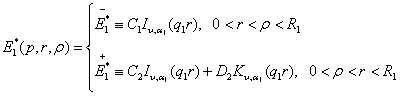 .
.
Властивості
(9) функції Коші дають алгебраїчну систему двох рівнянь:
![]()
![]()
Звідси
отримуємо співвідношення:
![]()
![]() (10)
(10)
Доповнимо рівності (10)
алгебраїчним рівнянням:
![]() (11)
(11)
Із системи (10), (11) знаходимо, що
![]()
![]()
![]()
Цим функція Коші ![]() визначена й внаслідок
симетрії відносно діагоналі
визначена й внаслідок
симетрії відносно діагоналі ![]() має структуру:
має структуру:
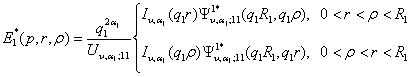 (12)
(12)
Нехай функція Коші
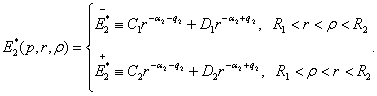
Властивості
(9) функції Коші дають алгебраїчну систему:
![]()
![]()
Звідси знаходимо співвідношення:
![]()
![]() (13)
(13)
Доповнимо
рівності (13) алгебраїчним рівнянням:
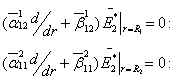
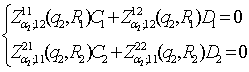 (14)
(14)
Внаслідок
рівностей (13) алгебраїчна система (14) набуває вигляду:
![]()
![]() (15)
(15)
Звідси
знаходимо, що
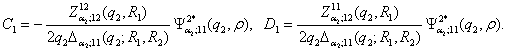
Цим
функція Коші ![]() визначена й внаслідок
симетрії відносно діагоналі
визначена й внаслідок
симетрії відносно діагоналі ![]() має структуру:
має структуру:
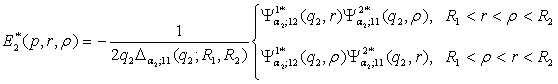 . (16)
. (16)
У
формулах (14)-(16) беруть участь функції:
![]()
![]()
![]()
![]()
Припустимо,
що функція Коші
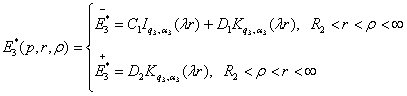 .
.
Властивості
(9) функції Коші дають алгебраїчну систему:
![]()
![]()
Звідси
знаходимо співвідношення:
![]() (17)
(17)
Доповнимо
рівності (17) алгебраїчним рівнянням:
![]() (18)
(18)
З
алгебраїчної системи (17), (18) маємо:
![]() .
.
Цим
функція Коші ![]() визначена й внаслідок
симетрії відносно діагоналі
визначена й внаслідок
симетрії відносно діагоналі ![]() має структуру:
має структуру:
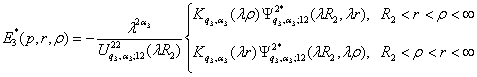 . (19)
. (19)
Умови
спряження (5) для визначення величин ![]() дають алгебраїчну
неоднорідну систему чотирьох рівнянь:
дають алгебраїчну
неоднорідну систему чотирьох рівнянь:
![]()
![]() (20)
(20)
У
системі (20) беруть участь функції
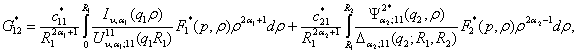
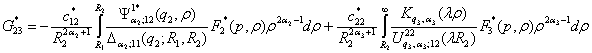
та символ Кронекера ![]()
Введемо
до розгляду функції:
![]()
![]()
![]()
![]()
Припустимо,
що виконана умова однозначної розв'язності крайової задачі (4), (5): для ![]() з
з ![]() , де
, де ![]() - абсциса збіжності
інтегралу Лапласа, та
- абсциса збіжності
інтегралу Лапласа, та ![]() визначник
алгебраїчної системи (20) відмінний від нуля
визначник
алгебраїчної системи (20) відмінний від нуля
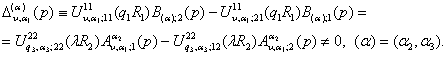 (21)
(21)
Визначимо головні розв'язки
крайової задачі (4), (5):
1)
породжені неоднорідністю умов спряження функції Гріна
![]()
![]()
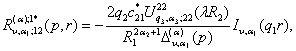

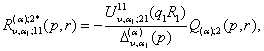
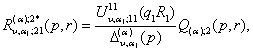 (22)
(22)
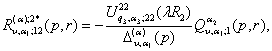
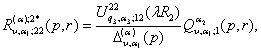
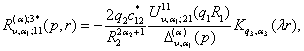

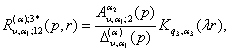
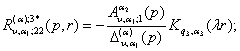
2)
породжені неоднорідністю системи (4) функції впливу
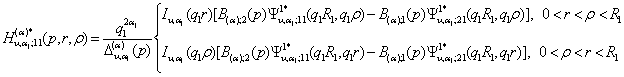
![]()
![]()
![]()
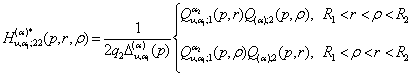 , (23)
, (23)
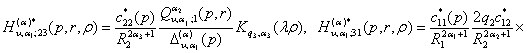
![]()
![]()
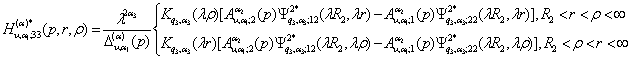 У результаті
однозначної розв’язності алгебраїчної системи (20), підстановки отриманих за
правилами Крамера [5] значень
У результаті
однозначної розв’язності алгебраїчної системи (20), підстановки отриманих за
правилами Крамера [5] значень ![]() та
та ![]() у рівності (8) й низки елементарних перетворень маємо єдиний
розв'язок крайової задачі (4), (5):
у рівності (8) й низки елементарних перетворень маємо єдиний
розв'язок крайової задачі (4), (5):
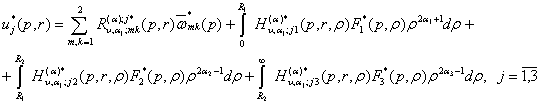 (24)
(24)
Повертаючись
в (24) до оригіналу, одержуємо єдиний аналітичний розв'язок параболічної задачі
(1)-(3):

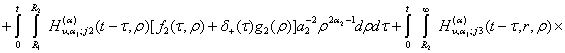
![]() (25)
(25)
У
рівностях (25) за означенням [4]
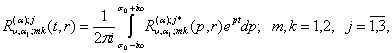 (26)
(26)
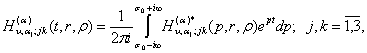 (27)
(27)
Знайдемо
коректний для використання вираз функцій ![]() та
та ![]()
Особливими точками функцій ![]() та
та ![]() є точки галуження
є точки галуження![]() та
та![]() Покладемо
Покладемо ![]()
![]() . Одержимо:
. Одержимо: ![]()
![]() де
де ![]() .
.
Якщо
![]() то
то ![]()
![]()
![]() ; якщо
; якщо ![]() , то
, то ![]()
![]()
![]()
![]() якщо
якщо ![]() , то
, то ![]()
![]()
![]()
Скористаємося
відомими функціональними співвідношеннями
![]()
![]()

![]()
![]()
![]()
Одержимо
в результаті елементарних підрахунків, що
![]()
![]() (28)
(28)
Якщо
![]() то згідно формул (26)
та (27) функції
то згідно формул (26)
та (27) функції ![]() і
і ![]() Згідно формул (25)
функції
Згідно формул (25)
функції ![]() Отже, розв'язок даної
параболічної задачі
Отже, розв'язок даної
параболічної задачі ![]() , що не можливо. Звідси випливає, що
, що не можливо. Звідси випливає, що ![]() І ми одержали
трансцендентне рівняння для обчислення власних чисел гібридного
диференціального оператора (ГДО)
І ми одержали
трансцендентне рівняння для обчислення власних чисел гібридного
диференціального оператора (ГДО)
![]() (29)
(29)
![]() - одинична функція
Гевісайда [7].
- одинична функція
Гевісайда [7].
Визначимо
величини та функції:
![]()
![]()
![]()
![]()
![]()
![]() (30)
(30)
![]()
![]()
![]()
Введемо до розгляду вагову функцію
![]() , (31)
, (31)
спектральну вектор-функцію
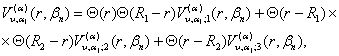 (32)
(32)
та її узагальнений квадрат норми
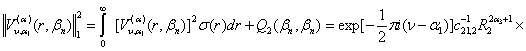
![]() (33)
(33)
За
узагальненою теоремою розвинення [4] маємо:
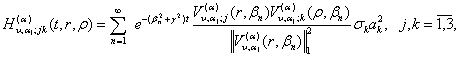 (34)
(34)
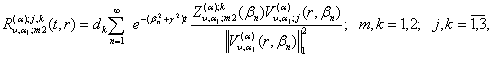 (35)
(35)
Тут прийняті позначення:
![]()
![]()
![]()
Інтегральне
зображення розв'язку даної параболічної задачі згідно формули (25) набуває
вигляду:
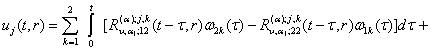
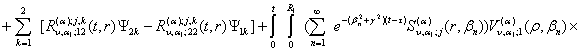
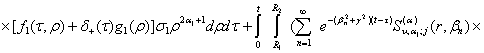
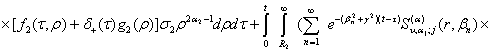
![]() (36)
(36)
Тут беруть участь функції
![]()
та дельта-функція ![]() , зосереджена в точці
, зосереджена в точці ![]()
Одержане
інтегральне зображення (36) аналітичного розв'язку параболічної задачі (1)-(3)
показує, що нами побудоване пряме ![]() та обернене
та обернене ![]() скінченне гібридне
інтегральне перетворення, породжене на множині
скінченне гібридне
інтегральне перетворення, породжене на множині ![]() ГДО
ГДО ![]()
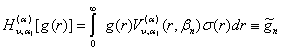 (37)
(37)
![]() (38)
(38)
Додамо
до цих правил основну тотожність інтегрального перетворення ГДО ![]()
![]() (39)
(39)
Правила
(37), (38) та (39) складають математичний апарат для розв'язання задачі (1)-(3)
методом скінченного гібридного інтегрального перетворення типу
Бесселя-Ейлера-(Конторовича-Лєбєдєва) із спектральним параметром за відомою
логічною схемою.
Список використаних
джерел:
1.
Тихонов А.Н. Уравнения
математической физики / А. Н. Тихонов, А.А. Самарский. – М.: Наука, 1972. –
735с.
2.
Ленюк М.П. Исследование
основных краевых задач для диссипативного волнового уравнения Бесселя / М.П.
Ленюк. – Киев, 1983. – 62с. – (Препринт / АН УССР. Ин-т математики; 83.3).
3.
Ленюк М.П. Інтегральні перетворення типу Конторовича – Лєбєдєва / М.П.
Ленюк, Г.І. Міхалевська. – Чернівці: Прут, 2002. – 280с.
4.
Лаврентьев М.А. Методы
теории функций комплексного переменного / М.А. Лавреньев, Б.В. Шабат. – М.:
Наука, 1987. – 688с.
5.
Курош А.Г. Курс высшей алгебры / А.Г.
Курош. – М.: Наука, 1971. – 432с.
6.
Степанов В.В. Курс
дифференциальных уравнений / В.В. Степанов. – М.: Физматгиз, 1959. – 468с.
7.
Шилов Г.Е. Математический анализ.
Второй специальный курс. / Г.Е. Шилов. – М.: Наука, 1965. – 328с.