Ибрагимов У.М., Тусеев Н.У.
Южно-Казахстанский государственный университет
им.М.Ауезова
задачи избежания столкновений в распределенных
управляемых системах
Введение. В настоящей работе рассмотрены задачи избежания
столкновений. При этом на управляющие параметры, входящие в правую часть
уравнения, налагаются различные ограничения (геометрические, интегральные,
смешанные). Из полученных четырех задач для первых двух ((6), (7) и (6), (8))
получены достаточные условия, гарантирующие избежания столкновений из всех
начальных положений. Для третьей задачи ((6), (9)) найдены два бесконечных
множества таких, что из начальных положений, принадлежащих первому множеству
невозможно избежания столкновений, а из точек второго возможно избежании
столкновений. Для четвертой задачи ((6), (10)) установлена возможность
избежания столкновений из произвольного начального положения.
В
пространстве 
рассматривается дифференциальный оператор 
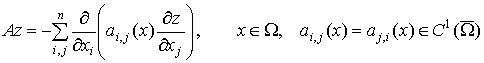вида [1]
(1)
где 
-ограниченная кусочно
гладкой границей область в 
. Областью оператора 
оператора 
является 
(пространство дважды
непрерывно дифференцируемых функций). Коэффициенты 
удовлетворяют
следующему условию: существует постоянная 
такая, что для всех 
и 
имеет место
неравенство
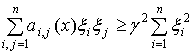. (2)
Положив 
, можно показать, что 
удовлетворяет всем
требованиям скалярного произведения.
Таким образом
превращается в
гильбертово пространство. Однако оно неполно относительно нормы
(3)
порожденной скалярным
произведением 
. Пополнив 
относительно нормы 
, мы получим полное гилбертово пространство, называемое
энергетическим пространством оператора 
.
Известно, [1,2], что при выполнении
условия (2) оператор 
имеет дискретный спектр, точнее,
имеет бесконечную последовательность обобщенных собственных чисел 
с пределем в
бесконечности и бесконечную последовательность обобщенных собственных функций 
составляющих полную
систему 
в пространстве 
. Мы будем считать 
, где 
-символ Кронекера.
Пусть 
-произвольное
неотрицательное число. Введем обозначения
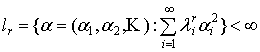
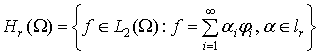(4)
В
пространствах 
, 
определим скалярные
произведения и нормы:
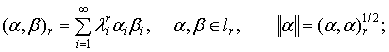
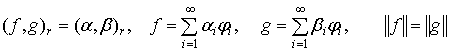(5)
Отметим, что 
и 
для произволных 
.
Через 
обозначим
пространство, состоящее из непрерывных (суммируемых с квадратом измерымых)
функций, определенных на 
и со значениями в 
, где 
-некоторая
положительная постоянная.
Постановка задачи. Рассмотрим следующую управляемую
распределенную систему [3,4]:
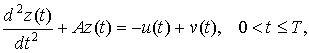
(6)
где оператор 
задан в виде (1).
В [2] установлено, что в
пространстве 
существует
единственная функция 
, являющейся решением задачи (6) в смысле теории обобщенных
функций (теории распределенных), при этом 
.
Функции 
и 
называются
управлениями противоборствующих сторон. Они удовлетворяют ограничениями,
определяемых одной из следующих систем неравенств:
(7)
(8)
(9)
(10)
где 
и 
-неотрицательные
константы.
Управления 
и 
, удовлетворяющие одному из условий (7)-(10), назовем
допустимыми. Управляемую систему (6), в которой 
и 
удовлетворяют неравенствам
(7)((8); (9); (10)), будем называть задачой (6), (7), ((6), (8); (6), (9); (6),
(10)).
Определение. Будем говорить, что в задаче
(6), (7), ((6), (8); (6), (9); (6), (10)) возможно избежание столкновения (с
конечным положением 0) из начального положения 
, если для произвольного, фиксированного положительного числа
можно построить
управление 
, такое что 1) 
в (6), (8) и (6),
(10); 
в (6), (9)); 2) для
произвольного управления 
, удовлетворяющего неравенству 
в (6), (8) и (6),
(9); 
в (6), (10)), решение
, задачи (6), где 
, 
, и его производная 
, одновременно не обращаются в 0. При этом для нахождения
значения 
управления 
в каждый момент
времени 
разрешается использовать
значения:
1) 
в (6), (7) и (6),
(9);
2) 
и 
, 
(
) при 
), в (6), (8);
3) 
, 
, 
, и 
, 
(
при 
, 
, 
при 
) в (6), (10), где 
-произвольное
положительное фиксированное число.
Задача
избежания столкновения состоит в нахождении начальных положений 
, из которых можно избежать столкновения (с точкой 0), а
также в явном построении управления 
.
Теорема. 1) Если 
, то в задачах (6), (7) и (6), (8) возможно избежать
столкновений из любого начального положения 
.
2) Для
произвольных 
и 
в задаче (6), (9) существуют
два бесконечных множества начальных положений таких, что из точек первого можно
обеспечить столкновения за конечное время, а из точек второго множества
возможно избежать столкновения.
3) Для
произвольных 
и 
в задаче (6), (10) возможно избежать столкновение из произвольного
начального положения 
.
Выводы.
Рассматривается задача избежания столкновений в системе, описываемой
управляемой уравнением в частных производных, содержащим производную второго
порядка по времени и эллиптический оператор. При этом управляющие параметры
аддитивно входят в правую часть уравнения. С помощью обобщенных собственных
чисел и обобщенных собственных функций данного эллиптического оператора вводятся
новые пространства, зависящие от неотрицательного параметра. Вводимые в
дальнейшем задачи изучаются во всей шкале этих пространств. Получены
достаточные условия для избежания столкновений в задачах получающихся при
различных ограничениях на управляющие параметры.
Литература
1.
Черноусько Ф.Л. Ограниченные управления в системах с распределенными
параметрами // Прикладная математика и механика, 1992. Т.56. Вып. 5. –с. 810-826.
2.
Авдонин С.А., Иванов С.В. Управляемость систем с распределенными
параметрами и семейства экспонент. -Киев : УМКВО, 1989. - 243 c.
3.
Ибрагимов У.М. Об избежании столкновений в распределенных управляемых
системах со смешанными ограничениями // Вестник КазНТУ им. К.Сатпаева, -Алматы,
№2 (84), 2011. с.178-184
4.
Ибрагимов У.М. Необходимые условия инвариантности относительно системы с
распределенными параметрами // Вестник ЕНУ им.Л.Н.Гумилова, -Астана, №2 (81),
2011. с.57-62.