Математика /4. Прикладная математика/

Ryaboshtan O.F., Milenin A.M., PhD, Skofenko S.M., PhD

Kharkiv Petro Vasylenko National Technical University of Agriculture

About surfaces of gas turbines and their corresponding differential equations

As is known, the design surface with the use of differential equations with partial derivatives is based on the close relationship of the equation, the characteristic of its lines and the integrated surface. This equation corresponds to a unique set of characteristic lines, of which the surface is constructed. But it is one and the same surface can be formed by another set of lines, and this corresponds to a different set of differential equation with partial derivatives.

Of course the problem of finding the whole set of differential equations, respectively, of the surface, is not easy.

Consider some of the issues of inter-differential equations, characteristics of surfaces and their properties.

It is known that the same surface can have the set of differential equations, each of which reflects one a law of its formation.

For the surface

(1)

regular in the domain of the independent variables, there corresponds an infinite set of differential equations I order depending on the type of the function F:

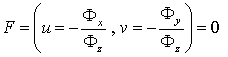(2)

Differential equation corresponds to an infinite set of integral surfaces, depending on the type of the initial curve and the complex formed from the characteristic lines.

Fix ation level of the set (2) allocates a given surface a one-parameter set of characteristic lines. On the other hand, the allocation of the surface characteristics of the one-parameter set is not uniquely determine the appropriate set of differential equation.

If multiple lines are specified as

(3)

then it corresponds to a linear differential equation with partial derivatives, an exemption from a and b (3) equation

(4)

Between the surface and its corresponding differential equation there is some relationship.

This relationship allows:

a) where equipment lines belonging to a given surface by its projection on the Oxy

(5)

determining equipment curve normal vector of the surface.

b) to find the point on the surface with the given parameters u and v, or, conversely, the values of u and v for a given point .

Surface induces normal map x, y plane to the surface u, v.

Analytical form of this correspondence is established, subject to:

(6)

Regular surface permits in the neighborhood of , where regular parameterization, which allows her to get the equation in the form

, (7)

Whence the equation of the normal mapping is obtained by differentiating (7)

, (8)

Actually, except for z, we will check the same transformations in the proposal that the requirements of regularity, are fulfilled.

For a first order differential equation, obtained exclusive of any two of the three variables x, y, z, this surface is integral.

There are three types of equations , and the equation of the same species may not be unique.