Высшие трансцендентные функции

при идентификации управляющих воздействий

Данилов А.М., Гарькина И.А.

Значительный интерес представляет установление взаимного соответствия между количественными (объективными) показателями качества управления и количественными значениями характеристик объекта. Когда техническая часть эргатической системы описывается системой линейных обыкновенных дифференциальных уравнений, имеющей пар комплексно-сопряженных корней, в большинстве случаев стиль управления оператора определяется собственными частотами и безразмерными коэффициентами демпфирования . При этом на каждом конкретном интервале времени стиль управления определяется по оценке оператором динамических характеристик объекта. Исходными предпосылками при ретроспективном анализе являются:

- характеристики объекта определяют стиль управления,

- имеется взаимно однозначное соответствие между стилем управления и некоторыми объективными показателями качества управления,

- известна оценка объекта адаптированными к нему операторами.

Это позволяет по известной оценке объекта определить область равной оценки, а по ней - интервалы возможных значений и ; совокупность объективных показателей качества управления легко устанавливаются по данным нормальной эксплуатации (наличие обратного соответствия требует специального экспериментального подтверждения для каждого транспортного средства).

С точки зрения теории управления стиль управления определяется соответствующим изменением передаточных функций оператора в зависимости от передаточных функций объекта. Экспериментальное установление вида этой связи на имитаторе объекта не вызывает принципиальных затруднений. Естественно, предполагается наличие предварительной адаптации оператора к каждому из проводимых изменений параметров имитаторов (оценка производилась на основе спектра ; - точки максимума). Определенные трудности возникают при определении показателей для оценки стиля управления для апериодических систем (в имитаторах для увеличения его устойчивости и управляемости модель динамики объекта обычно передемпфирована по сравнению с реальным объектом).

Представляет существенный интерес возможность использования и других объективных показателей качества управления. Если для колебательных систем в качестве показателей используются величины, фактически зависящие от параметров разложения средневзвешенной детерминированной функции в ряд Фурье, то это будут показатели, являющиеся функциями от коэффициентов Фурье разложения по некоторой ортогональной системе ; 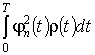- сходятся.

Если функция задана на интервале , то наилучшим ее приближением будет

,

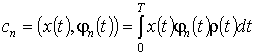
(минимальное значение ошибки 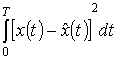достигается при этих значениях , при ; если получим равенство Парсеваля 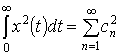, ). При этом можно ограничиться аппроксимацией конечным числом членов; определяется по допустимой ошибке. Указанное распространяется на описание динамических свойств как линейных, так и нелинейных квазистационарных систем. Наиболее употребительными являются разложения функций по двум ортонормальным системам: по полиномам Ляггера и Чебышева.

При разложении по полиномам Ляггера с весом

(;).

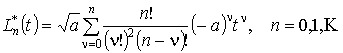Такое разложение обладает перед другими значительным преимуществом, поскольку позволяет весьма просто определить передаточную функцию разомкнутой системы. Действительно, преобразование Лапласа функции имеет вид £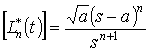, так что для частной суммы 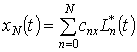справедливо:

££.

Аналогично для имеем:

££.

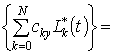
Так что передаточная функция разомкнутой системы представится в виде

=.

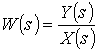Определенными преимуществами обладает и разложение по ортогональным полиномам Чебышева (обладают «свойством почти равных ошибок»: ошибка аппроксимации колеблется внутри диапазона измерений между двумя почти одинаковыми пределами). Задача оценка качества управления здесь так же сводится к идентификации нелинейного процесса , с помощью ортогональных полиномов: определяются коэффициенты аппроксимирующего уравнения

; , ;

, ; .

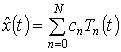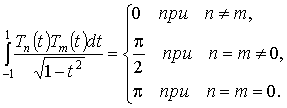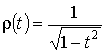Справедлива рекуррентная формула

().

Практически по данным нормальной эксплуатации управляющие воздействия можно получить в интервале времени . Поэтому введем новую переменную , . Тогда аппроксимирующее процесс уравнение представится в виде

.

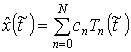Коэффициенты определятся по методу наименьших квадратов на основе минимизации 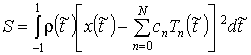, что дает

, , .

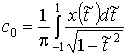Здесь коэффициенты Фурье не зависят от выбора ; изменение не требует пересчета , . Выбор наилучшего значения производится из условия , . Алгоритм идентификации основывается на дискретных значениях управляющих воздействий и фазовых координат, полученных по осциллограммам в точках .

Оценка имитационных характеристик модели производилась по отклонению коэффициентов частичных сумм для управляющих воздействий оператора в реальных условиях и на модели объекта. По данным независимой экспертизы результаты признаны удовлетворительными.