Формализация оценочной шкалы Купера-Харпера

Данилов А.М., Гарькина И.А.

Ограничимся рассмотрением короткопериодической составляющей продольного движения. Она приближенно описывается системой уравнений

,

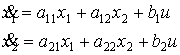(принято: ).

Для объективизации оценки оператором устойчивости и управляемости объекта предлагается использовать функционал качества

.

Введя 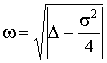,, , ,, получим

,

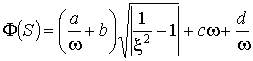- весовые константы.

На практике возникает задача по оценке влияния параметров системы управления на оценку оператором качества объекта. После соответствующих преобразований в этом случае уравнения движения представляются в виде

Здесь

- компоненты вектора управления;

- входные воздействия;

- коэффициенты усиления.

Введя новые переменные

,

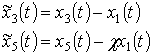уравнения движения представим в виде:

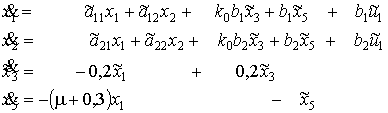
( рассматривается как входной сигнал).

Здесь

;

.

Из первого и четвертого уравнений следует:

При небольшом времени регулирования и малых значениях зависимость и от слабая (зависимость от практически отсутствует). Поэтому и можно рассматривать как входные воздействия в системе с матрицей . Свойства системы полностью определяются матрицей , а зависимость от параметров системы управления можно численно установить по формулам перехода от к . В частности,

,

.

С учетом 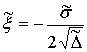, 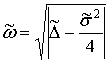легко определить траекторию движения точки на плоскости . Экспериментально было установлено, что классу по шкале Купера-Харпера (Cooper-Harper rating scale) соответствует , а соответствует .

Если - некоторая точка, лежащая на границе -го класса ,то ей соответствуют значения и , определяемые соотношениями:

, ;

,

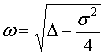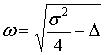(соответственно для колебательной и апериодической систем).

Для колебательной системы имеем:

,, .

В силу предыдущего

, , .

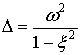Аналогично для апериодических систем

, ,.

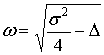Так что

, , .

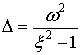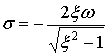Для системы с матрицей имеем:

,

.

Для колебательной системы

,

.

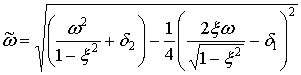Аналогично для апериодических систем

, .

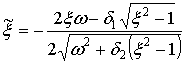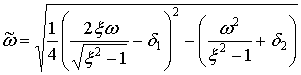При малых приращениях и будем иметь:

, .

Для колебательной системы

,	;
,	.

Таким образом,

, .

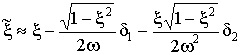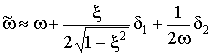Аналогично для апериодических систем получим

, .

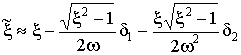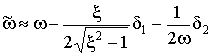Как видим, подбором параметров интегральных характеристик и системы управления можно улучшить класс системы.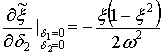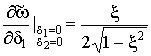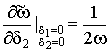