Математическое обеспечение безотказности элементов знаний, умений и навыков

Л.Г. Поляков, Е.М. Тишина, Г.С. Слюсар

Пензенский государственный университет архитектуры и строительства

В данной статье рассматривается один из возможных математических подходов количественной оценки безотказности знаний специалистов. Основным принципом оценки является расчленение общей задачи на элементы решения и определения их количественных значений показателей безотказности (вероятность безотказности полученных знаний). Далее на основе этих значений, с использованием теории надежности, производиться оценка элементов знаний специалиста.

Ключевые слова: математическое обеспечение, безотказность, надежность, знания, специалисты.

Подготовка высококвалифицированных специалистов неразрывно связано с качеством их профессиональной подготовки, т.е. с надежностью обучения. Одним из составляющих свойств надежности обучения является безотказность применения полученных знаний, умений и навыков на практике [1]. Под безотказностью обучения предлагается понимать свойство процесса обучения, который позволяет непрерывно сохранять возможность использования полученных знаний, умений и навыков в течение некоторого (заданного) времени. (В дальнейшем под понятием сочетания «Знание, умение и навыки» будем использовать термин «Знание»).

Для всесторонней количественной оценки этого свойства обучения возникает необходимость рассмотрения процесса реализации полученных знаний (процесс решения задач), т.е. умение решение задач.

Решение любой задачи, в общем случае, представляет собой выполнение отдельных операций (шагов). Если введем понятие элемент решения, тогда решение задачи в целом есть система взаимодействия элементов. Под элементом решения следует понимать один шаг решения задачи, заключающийся в применении конкретной формулы, отдельной операции, использования отдельного навыка или умения, принятие промежуточного решения по принципу «да – нет» и т.п. Говоря другими словами, шаг это элементарное действие или этап в процессе решения задачи. Если элементарное действие это шаг решения задачи тогда совокупность элементов решение задачи в целом это система, а их соединение есть последовательность решения задачи.

Учитывая, определения элемент и система, то показатели безотказности можно подразделять на показатели безотказности элементов и показатели безотказности систем знаний, умений и навыков.

В данной статье рассматривается только показатели безотказности, применительно к элементам знаний. Для дальнейших рассуждений введем понятия «Работоспособное состояние» и «Состояние отказа» уровня знаний испытуемого в текущий момент времени. Если под работоспособным состоянием элемента или системы понимать такое состояние уровня знаний испытуемого, при котором он может достичь положительного результата решения, то не возможность получения положительного решения будет являться состоянием отказа элемента или системы.

Согласно теории надежности [2, 3] для всесторонней количественной оценки этого свойства надежности, применительно к элементам, наиболее подходящими показателями лучше всего использовать вероятность безотказности полученных знаний, вероятность утраты знаний, интенсивность утраты знаний, параметр потоков утраты знаний, среднее время утраты знаний и среднее время безотказности знаний.

Вероятность безотказности полученных знаний (ВБЗ) – является основным показателем безотказности и он определяет вероятность того, что в пределах заданного времени утрата знаний не произойдет. Символически это можно записать в таком виде

р(t)=р(Q>t₁), (1)

где Q – случайное время возникновения утраты знаний;

t₁ – заданное время.

Кроме ВБЗ, при оценке безотказности используется и другая вероятность – вероятность утраты знаний (ВУ). Это вероятность события, противоположного безотказности в знаниях. Вероятность утраты (ВУ) называется вероятность того, что случайное время возникновения утраты знаний Q окажется меньше заданного времени t₂, т.е.

q(t)=p(Q<t₂). (2)

Из теории вероятности известно, что сумма вероятностей для противоположных событий (утрата – безотказность) равна 1, т.е.

р(t)+q(t)=1. (3)

Практически ВБЗ можно определить по следующей статистической формуле:

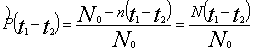, (4)

где N₀ – число испытуемых до начала наблюдений;

t₁-t₂ – отрезок времени, в течении которого велись наблюдения;

n(t₁-t₂) – число испытуемых, утративших знания за время (t₁-t₂).

По формуле (4) можно определить ВБУ только за отрезок времени (t₁-t₂) и невозможно определить р(t) за другой период времени и тем более нельзя предсказать ее в бедующем.

Если принять во внимание, что ВБУ подчиняется экспоненциальному закону распределения, то его можно характеризовать интенсивностью утрат знаний l(t). Под интенсивность утрат знаний следует понимать отношение числа испытуемых n(t), утративших знание в единицу времени, к среднему числу испытуемых, не утративших знание в данный отрезок времени Δt при условии, что утратившие знания не восстанавливают их, т.е.

, (5)

где n(Δ t) – число испытуемых, утративших знание за время Δ t;

, (6)

здесь N(t) – число испытуемых до начала испытаний;

N(t+ Δ t)=N(t)-n(Δ t) – количество испытуемых не утративших знания во время и после испытаний.

Следующий показатель, характеризующий безотказность знаний является среднее время утраты знаний – Т_ср(t). Этот показатель применяется при условии, что испытуемые в процессе испытаний утерянные знания восстанавливают.

Среднее время утраты знаний (СВУЗ) называется математическое ожидание времени до первой утраты знаний

Практически величину можно определить по следующим статистическим формулам.

Для случая, когда все испытуемые утратили необходимые знания

, (7)

где N₀ – число испытуемых;

t_i – время до i-ой утраты знаний.

Для случая, когда испытания проводятся для определенного промежутка времени Т_ср. При этом часть испытуемых утратила полученные знания, а другие не утратили. Формула имеет вид

, (8)

где т – количество испытуемых утративших знания.

В случаях, когда испытания проводятся до получения заданного количества утрат знаний – r. При этом N₀-r испытуемых свои знания не утратили. Расчет можно произвести следующим образом

, (9)

где t_r – время последней (r-ой) утраты знаний.

При условиях, когда в процессе испытаний утраченные знания восстанавливаются, то для оценки безотказности использования знаний необходимо использовать параметр потоков утраты знаний и среднее время безотказности знаний.

Параметр потоков утраты знаний (ППУ) называется отношение числа испытуемых утрачиваемых знания в единицу времени, к числу испытуемых при условии, что все испытуемые утратившие знания их восстанавливают и продолжают учувствовать в испытаниях. На основании этого утверждения имеем

, (10)

где n_Σ(t) – число всех отрезков, получаемых за время Δ t.

Если считать, что ППУ для каждого испытуемого является простейший , т.е. характеризуется тремя основными свойствами: стационарностью, ординарностью и без последствия:

а) если ω(t)=const, то поток считается стационарным;

б) если вероятность одновременного возникновения двух утрат знаний близка к нулю, то поток называется ординарным;

в) Если утраты знаний независимы, то поток считается без последствия.

Применяя эти утверждения к каждому испытуемому в отдельности, становится очевидным, что поток простейший. Следовательно, для простейшего потока (ВУ) принимает закон Пуассона

, (11)

где Р_т – вероятность возникновения т утерь знаний за время t.

Если положить т=0 (не возникает ни одной потери знаний), что означает р₀ – вероятность утраты знаний за время t, то получаем

р₀=р(t)=e^-ωt. (12)

По этой формуле можно определять р(t) только для простейшего потока потери знаний.

Среднее время безотказности знаний (СВБЗ). Будем считать, что СВБС есть отношение суммарного времени использования испытуемого к математическому ожиданию его потерь знаний в течении этого времени. Из этого определения следует

, (13)

где М[r(t_Σ)] – математическое ожидание числа утрат знаний r(t_Σ);

t_Σ – суммарное время использования.

Практически СВБЗ определяется по формуле

, (14)

где r(t_Σ) – число утери знаний, наступивших в течении времени t_Σ.

Для стационарного потока утраты знаний формула (14) имеет следующий вид:

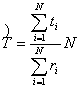, (15)

где .

Формула (14) применима для полной выборки [NиN].

В случае, когда количество испытуемых (N₀) велико расчет величины Т удобнее определять по следующей формуле:

, (16)

где t_r – наибольшее время последнего r-го отказа;

t_r – время (наибольшей) последней r-ой утраты знаний;

r – количество всех отказов за время t_r.

Таким образом, используя статистические данные по усвоению полученных знаний всегда можно оценить количественно и качественно безотказность элементов системы знаний при подготовке специалистов. Кроме того, появляется возможность управления самим процессом обучения исходя из условий изменения требований предъявляемым к специалистам.

Список используемой литературы

1. Л.Г. Поляков, Е.Е. Петрикова. К вопросу о безотказности использования полученных знаний. Сборник статей 1 городской межвузовской научно-практической конференции. Молодежь ХХI столетия: вопросы образования, воспитания и социализации. - Пенза: ПГПУ, 2010

2. Надежность технических систем: Справочник. Ю. К. Беляев, В. А. Богатырев, В. В. Болотин и др.; Под ред. И. А. Ушакова. - М.: Радио и связь, 1985. - 608 с, ил.

3. Справочник по расчету надежности машин на стадии проектирования /Б.Ф. Хазов, Б.А. Дедусев. -. М.: Машиностроение, 1986.