Наука и образование. Физика.

Рыжакова Л.В.

Доцент кафедры ОТД МФ Иркутского государственного технического университета, Россия

Dunia Safi Olivia

Lycee Boyokani, Kinshasa,Сongo

Методика определения массы криволинейного столба жидкости в поле силы тяжести.

Применение задач кинематики для расчета какого-либо параметра материального тела имеет большой интерес. Рассмотрим движение тела вблизи поверхности Земли, происходящее с постоянным ускорением свободного падения g. Уравнения движения в кинематике не учитывают массу тела. Используя кинематические уравнения, рассчитаем массу тела с переменным объемом, связав материальную точку с элементом объема. Поставлена следующая задача: из шланга, лежащего на земле, бьет струя воды с начальной скоростью v₀ под углом к горизонту. Определить массу воды, находящуюся в воздухе. Площадь поперечного сечения шланга s. Задача эта относится к классу нестандартных задач, т. к. вначале для ее решения мы принимаем условие, что тело является просто материальной точкой, а затем учитываем размер этого тела.

Используя кинематические уравнения, рассчитаем массу тела с переменным объемом, связав материальную точку с элементом объема.

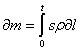, (1)

где - элемент пространственной кривой, которая представляет собой параболу, . Будем считать, что кривая интегрирования задана гладкой, а плотность в каждой точке кривой - непрерывной и постоянной величиной. Тогда система уравнений рассматриваемого движения имеет вид:

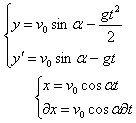(2)

И для элемента массы можем записать:

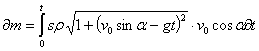(3)

Чтобы вычислить данный криволинейный интеграл введем новую переменную

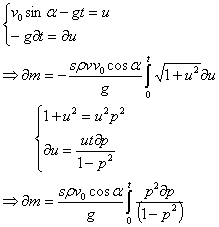(4)

Масса выделенного криволинейного столба жидкости в воздухе будет равна

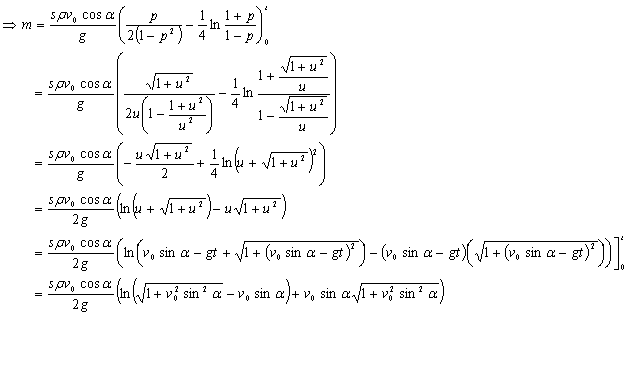
m= (5)

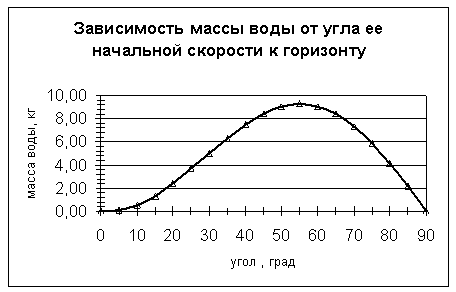
Рис.1 Зависимость массы воды от угла.

Анализ решения.

Из формулы (5) и рис.1 видно, что масса зависит только от начальной скорости потока жидкости и угла при условии, что площадь поперечного сечения шланга равна площади поперечного сечения водяной струи и практически на всем пути постоянна. При этом кривая графика показывает, что максимальная масса воды, находящуюся в воздухе, достигается при условии, что начальная скорость струи воды будет составлять с горизонтом угол не 45 градусов, как дают классические расчеты по кинематике, а угол 55 градусов к горизонту.

Литература.

1.Демков В.П, Третьякова О.Н Физика. Теория. Методика. Задачи. М.: Высшая школа. 2001. – 669с

2.Смирнов В.И. Курс высшей математики. М.: Наука. 1974 (т.1,2)

3.Смирнов В.И. Курс высшей математики. М.: Наука. 1974 (т.3,ч.1)