Д. т. н., професор Нагорний В.П., к. т. н. Денисюк І.І., Ліхван В.М.

Інститут геофізики ім. С.І. Суботіна НАН України

ДИНАМІКА АКУСТИЧНИХ ХВИЛЬ В ГАЗОРІДИННОМУ СЕРЕДОВИЩІ НА ПІЗНІЙ СТАДІЇ ЕКСПЛУАТАЦІЇ НАФТОВИХ РОДОВИЩ

Відомо, що в процесі експлуатації нафтового покладу пластовий тиск у продуктивному пласті знижується. Якщо зниження тиску відбувається до величини, нижчої від тиску насичення нафти газом, із нафти виділяється газ, що раніше знаходився в розчиненому стані. При цьому в нафтоносному пласті спостерігається пухирцевий режим течії з низьким коефіцієнтом нафтовіддачі.

Пухирцеві режими течії рідин досить детально досліджено в роботах [1–5]. Відмічається, що у випадку неньютонівських рідин при невеликих за масою та об’ємом домішках пухирців газу спостерігається явище зміни фізичних властивостей рідини [4].

Одна із особливостей середовища із пухирцями в процесі його обробки імпульсною дією – поява збудження в середовищі хвиль тиску, параметри яких залежать від виду навантаження і розміру пухирців.

У нашій роботі розглянуто взаємодію акустичної хвилі з пухирем газу і пульсацію газового пухиря у результаті такої взаємодії.

В задачі не розглядається схлопування пухиря і супутніх цьому процесу явищ. Середовище знаходиться в докавітаційному режимі. Припускається, що рідина насичена газом так, що у всьому об’ємі рідини постійно підтримується певна концентрація пухирів із газом. Під впливом акустичної хвилі, що проходить через це середовище, стінки газових пухирів здійснюють вимушені коливання. Нехтуємо взаємодією пухирів і обмежимося розглядом поодинокого пухиря із газом.

Для вивчення нелінійних хвильових процесів у середовищі, що розглядається, рівняння гідродинаміки повинні бути доповнені рівнянням малих коливань пухиря із газом у воді.

Вважаючи рідину ідеальною, в одномірному випадку система рівнянь Ейлера має вигляд:

;

(1)

,

(2)

де ρ – густина суміші води плюс газ; p – тиск у середовищі, що оточує пухир; υ – швидкість руху середовища.

Рух стінки пухиря у випадку нестисливої рідини описується рівнянням Релея:

,

(3)

де R – радіус пухиря; ρ₀ – густина рідини; – тиск газу в пухирі. Крапками позначені похідні за часом.

Враховуючи, що об’єм V пухиря газу

,

(4)

представимо рівняння (3) відносно параметра V.

Із виразу (4):

.

(5)

Використовуючи співвідношення (5), знаходимо:

; .

(6)

Підставивши співвідношення (5) і (6) у рівняння (3), після алгебраїчних перетворень отримаємо:

,

(7)

де

.

Зміна тиску в навколишньому середовищі викликає пульсацію пухиря. Припустимо, що відхилення тиску від рівноважного значення, а також коливання пухиря малі, тобто

; ;

(8)

<<1; <<1.

(9)

Якщо нехтувати теплообміном між пухирем із газом і оточуючим середовищем, то процес можна вважати адіабатичним і записати рівняння стану для газового пухиря у вигляді:

,

(10)

де γ – показник адіабати газу; ( і – питомі теплоємкості газу при постійному тиску і об’ємі, відповідно).

Підставляючи вирази (8) і (10) у рівняння (7) і зберігаючи малі члени порядку , отримаємо рівняння для малих коливань ідеального пухиря:

,

(11)

де 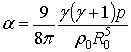, , 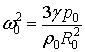, , 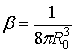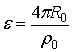R₀ – рівноважне значення радіусу пухиря.

Змінні V і p, штрихи над якими опущені, тут і в подальшому характеризують збурення об’єму і тиску.

Як видно з рівняння (11), нелінійний характер малих коливань газового пухиря обумовлений двома причинами: нелінійністю рівняння стану газу в пухирі αV ² і динамічною нелінійністю . У найбільш загальному випадку необхідно також враховувати дисипацію енергії в процесі коливання пухиря. Для цього доповнимо рівняння (11) членом, пропорційним швидкості зміни об’єму пухиря:

.

(12)

Згідно роботи [6] нелінійність, що обумовлена наявністю газових пухирів, в 10³–10⁴ разів перевищує нелінійність гідродинамічного характеру. Тому рівняння (1) і (2) можуть бути лінеаризовані. При цьому густина суміші ρ може бути ототожнена з рівноважною густиною рідини ρ₀. Врахування відхилення значення густини суміші ρ від значення ρ₀ призведе лише до нелінійних поправок, не суттєвих при лінеаризації рівнянь. Однак, при обчисленні похідної необхідно мати зв'язок густини суміші з іншими макроскопічними характеристиками середовища.

Густина суміші при концентрації пухирів n може бути в рівноважному випадку представлена у вигляді [6]:

,

(13)

де U – повний об’єм суміші; m – повна маса суміші; ρ_р і ρ_п – густини рідини і газу, відповідно.

Зміна об’єму суміші під дією поля акустичної хвилі або при пульсації газових пухирів визначається рівнянням

(14)

Коефіцієнт κ характеризує стисливість рідини .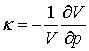

У розрахунку на одиницю об’єму із виразу (14) маємо

(15)

Підставляючи у формулу (15) значення у відповідності з виразом (13), знайдемо за умов <<1 і

(16)

З лінеаризованих рівнянь (1) і (2) з урахуванням (16) маємо:

,

(17)

де с₀ – швидкість розповсюдження звуку в рідині.

Таким чином, динаміка акустичної хвилі в рідині з пухирями буде описуватися системою рівнянь (11) і (17).

Аналітичний розв’язок цих рівнянь неможливий.

Розглянемо лінійне рівняння, яке визначається з виразу (11):

.

(18)

Із (18) отримуємо

.

(19)

У цьому випадку рівняння (17) і (19) можна звести до виразу:

, або .

(20)

Припустимо, що закон зміни об’єму газового пухиря в полі акустичної хвилі заданий у вигляді

,

(21)

де – початковий об’єм газового пухиря; ω – кругова частота пульсацій газового пухиря.

Розв’язок неоднорідного рівняння (20) складається з розв’язку однорідного рівняння

(22)

і часткового розв’язку неоднорідного рівняння (20).

Розв’язок однорідного рівняння (22) при нульових початкових умовах і при граничній умові p(0,0) = p_m такий:

,

(23)

де ; k – довільне постійне число (k > γ).

Частковий розв’язок неоднорідного рівняння (20) визначимо, використовуючи методи операційного числення.

Запишемо рівняння (20) в зображеннях за Лапласом при нульових початкових умовах з урахуванням співвідношення (21):

.

(24)

Рівняння (24) перетворимо до вигляду

,

(25)

де .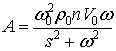

Використовуючи метод варіації постійних, частковий розв’язок неоднорідного рівняння (25) знаходимо у вигляді:

.

(26)

Розв’язок (26) представлений в зображеннях за Лапласом. Використовуючи формули операційного числення, із (26) знаходимо оригінал часткового розв’язку неоднорідного рівняння (20):

.

Отже, загальний розв’язок рівняння (20) має вигляд:

.

(27)

Із виразу (27) видно, що резонансна частота ω пульсацій газового пухиря залежить від швидкості розповсюдження звуку в рідині с₀, радіусу газового пухиря R₀ і концентрації пухирів n в рідині. Враховуючи раніше введене позначення для l, знаходимо:

.

Таким чином, при відбувається різке зростання амплітуди пульсацій газового пухиря, в результаті чого підсилюється амплітуда хвильового процесу обробки газорідинного середовища, що сприяє послабленню зв’язку рідин з твердою фазою нафтового пласта, зниженню в’язкості нафти і супроводжується покращенням її припливу на вибій свердловин і підвищенням їх дебіту.

Література:

1. Волны в жидкости с пузырьками /А.А. Губайдуллин, А.И. Ивандаев, Р.И. Нигматулин, Н.С. Хабеев // Итоги науки и техники. ВИНИТИ.– 1982. – Т. 17. – С. 160–249. – (Сер. Механика жидкости и газа).

2. Крайко А.Н. Механика многофазных сред / А.Н. Крайко, Р.И. Нигматулин, В.К. Старков, Л.Е. Стернин // Итоги науки и техники. ВИНИТИ. – 1972. – Т. 6. – С. 93–174. – (Сер. Гидромеханика).

3. Batchelor G.K. Compession waves in a suspension of gas bubbles in liquid // Fluid Dynamics Transactions. – 1969. –V 4. – № 1. – P.65–84.

4. Поздеев В.А. Импульсные возмущения в газожидкостных средах / В.А. Поздеев, Н.М. Бескаравайный, В.Г. Ковалев. – К.: Наук. думка, 1988. – 116 с.

5. Накоряков В.Е. Распространение волн в газо-и парожидкостных средах / В.Е. Накоряков, Б.Г. Покусаев, И.Р. Шрейбер. – Новосибирск: Институт теплофизики, 1983. – 238 с.

6. Руденко О.В., Солуян С.И. Теоретические основы нелинейной акустики. – М.: Наука, 1975. – 288 с.
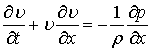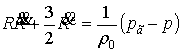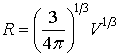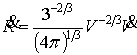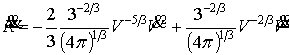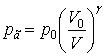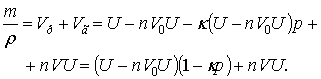
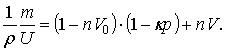
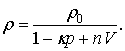
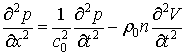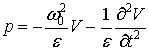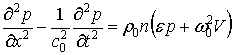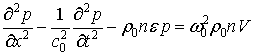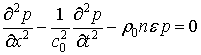
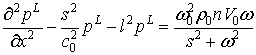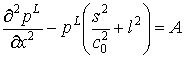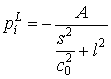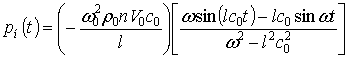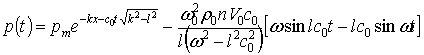