КЕРУВАННЯ ПРОЦЕСОМ КОНТАКТНОЇ МЕМБРАННОЇ ДИСТИЛЯЦІЇ В УМОВАХ НЕВИЗНАЧЕНОСТІ ЗА ДОПОМОГОЮ μ – РЕГУЛЯТОРА

Ладієва Л.Р., Дубік Р.М.

НТУУ «Київський політехнічний інститут», lrynus@yahoo.com

Керування процесом контактної мембранної дистиляції (КМД) ускладнюється з часом експлуатації через зміну характеристик мембрани таких як коефіцієнт поруватості та усереднений коефіцієнт теплопередачі. Синтез закону керування мембранним модулем (ММ) в умовах невизначеності, проводився з метою підвищення робастності перехідних характеристик, що актуально для керування процесом. Для розв’язку поставленої задачі досліджувалась можливість застосування H_∞ регулятора.

Ставилась задача розробки системи керування з μ – регулятором (для лінеаризованої моделі). В якості регульованого параметра обрано перепад температур розчину та дистиляту.

Невизначеність параметрів суттєво вливає на теплопередачу в ММ, що відбувається шляхом конвекції, а також на потік пари через пори мембрани. Усереднений коефіцієнт теплопередачі визначався виразом

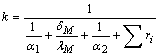, (1)

де α₁, α₂ – відповідно коефіцієнти тепловіддачі від розчину до мембрани і від мембрани до дистиляту Вт/(м²∙К); δ_M, λ_M – товщина мембрани, м та її коефіцієнт теплопровідності Вт/(м∙К); Σr_i – сумарний термічний опір забруднень (м²∙К)/Вт.

Математичний опис ММ складається на основі матеріальних і енергетичних потоків процесу [1]. Отримали математичний опис динаміки об’єкту у вигляді системи рівнянь з виділеним каналом керування:

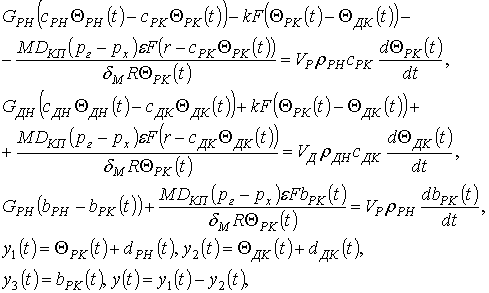(2)

де d_РК(t), d_ДК(t) – вихідні збурення за каналом розчину та дистиляту; y₁(t), y₂(t) – вимірювання температури розчину та дистиляту; y₃(t) – вихідна концентрація розчину; y(t) – параметр керування; де G_РН = u_РSρ_РН – витрата розчину солі на вході в ММ, кг/с; G_РК = u_РSρ_РК – витрата розчину солі на виході з ММ, кг/с; S = dh – поперечна площа каналу розчину, м²; d – ширина каналу, м; h – висота каналу, м; u_Р – швидкість подачі розчину м/с; ρ_РН, ρ_РК – густина розчину на вході і на виході ММ, кг/м³; c_РН, c_РК – теплоємкість розчину на вході і на виході з ММ, Дж/(кг∙К); Θ_РН – температура розчину солі на вході в ММ, К; Θ_РК, Θ_ДК – температура розчину і дистиляту на виході з ММ, К; k – коефіцієнт теплопередачі від розчину до дистиляту, Вт/(м²∙К); F – площа мембрани, м²; ε – коефіцієнт поруватості мембрани; J_Р – питомий масовий потік пари, кг/(м²∙с); r – питома теплота пароутворення, Дж/кг; V_Р – об’єм каналу розчину, м³; G_ДН = u_ДSρ_ДН – витрата дистиляту на вході в ММ, кг/с; G_ДК = u_ДSρ_ДК – витрата дистиляту на виході з ММ, кг/с; u_Д – швидкість подачі дистиляту м/с; ρ_ДН, ρ_ДК – густина дистиляту на вході і виході з ММ, кг/м³; c_ДН, c_ДК – теплоємкість дистиляту на вході і на виході з ММ, Дж/(кг∙К); Θ_ДН – температура дистиляту на вході в ММ, К, V_Д – об’єм каналу дистиляту, м³; b_PH, b_PK – відповідно початкова і кінцева концентрація солі кг/кг.

Записана математична модель процесу КМД (2) є нелінійна по відношенню до температури розчину на виході з модуля, яка входить також у знаменник в складову рівнянь, що враховує потік пари через мембрану.

Рівняння стану процесу КМД записані в наступному вигляді

(3)

де X = [Θ_РК Θ_ДК b_РК]^T – вектор стану; u = Θ_РН – керування; V = [v₁₅ v₁₆ v₂₅ v₂₆ v₃₅ v₃₈]^T – вектор вхідних збурень; v_ij – збурюючи фактори; початкові умови: X|_{t = 0} = [Θ_РН Θ_ДН b_РН]^T; матриці аналізу станів мають вигляд

; ; ,

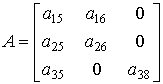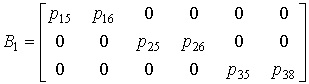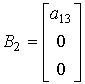де a_ij – коефіцієнти лінеаризованої моделі [1]; p_ij – параметри відносних збурень коефіцієнтів моделі.

Рівняння похибок, що спричинені невизначеностями

. (3)

Рівняння вимірювання виходу об’єкту має вигляд

, (4)

де D₁₁, D₁₂, D₂₁, D₂₂ – матриці прямих прямих зв’язків (нульові); d = d_РК – d_ДК – шум вимірювання перепаду температур; d_РК, d_ДК – шуми вимірювання температури розчину та дистиляту; r – задане значення перепаду температур розчину та дистиляту (Θ_РК – Θ_ДК); матриці виходу

; .

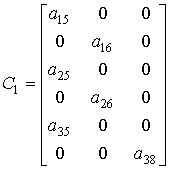Тобто опис об’єкту складається з четвірки матриць

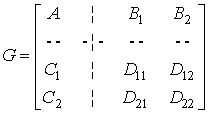. (5)

Систему (2) – (4) з урахуванням (5) представлено у вигляді верхнього дробово-лінійного перетворення F_U

y = F_U(G,Δ)u, (6)

де Δ = diag(δ_ij) – діагональна матриця невизначеностей; –1 ≤ δ_ij ≤ 1 – параметри невизначеності.

Керуючий вплив обчислювався у вигляді

u(p) = K(p)y(p), (7)

де K(p) – матрична ланка зворотного зв’язку; p – змінна Лапласа.

Процедура синтезу H_∞ регулятора ґрунтується на послідовному розв’язанні двох рівнянь Ріккаті для регулятора та спостерігача.

Для системи керування з H_∞ регулятором висувалися наступні вимоги

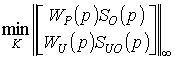, (8)

де S_O(p) = (I + G(p)K(p))^-1 – чутливість;

S_UO(p) = K(p)(I + G(p)K(p))^-1 – чутливість до керування; W_P(p), W_U(p) – вагові функції виходу системи та керування.

Математична форма вагових функцій обиралася безпосередньо за вимогами, що висувалися до характеристик системи у частотному та часовому просторі. Зокрема використано стандартний запис цих функцій

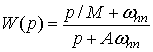, (9)

де M – допустиме пікове значення функцій чутливості (8) на межі смуги частот ω_nn; A – верхня межа мінімальної статичної похибки.

Вихідні сигнали в системі обчислювалися у вигляді

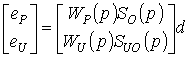, (10)

де e_P, e_U – вихід замкненої системи та керування.

Система, задовольняє вимогам робастної стійкості

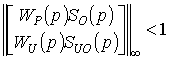. (11)

Процедура синтезу μ – регулятора починалась з розгляду питання робастної стійкості, прийнято, що D(jω) – деяка діагональна матриця (матриця масштабування), що комутує з Δ(jω), тоді

. (12)

Урахування (12) робастна стійкість набуває наступного вигляду

, (13)

де – множина матриць, що комутує з Δ(jω); F_L(P,K) – нижнє дробово-лінійне перетворення.

Знаходилась така матриця D, що нерівність (11) була менша нерівності (13), тим самим досягався найбільший запас робастної стійкості.

Сама процедура μ – синтезу виконувалась за допомогою методу D-K ітерацій, який складається з двох процедур оптимізації, що виконуються послідовно. Вони називаються: D – кроком та K – кроком відповідно. Пошук починається з K-го кроку:

1. Для фіксованої матриці D(jω), що на початку циклу приймалась одиничною, вирішувалась задача мінімізації H_∞ – норми

, (14)

де K₀ – множина регуляторів, що стабілізують об’єкт керування (знаходиться за допомогою H_∞ – синтезу, що базується на розв’язку двох рівнянь Ріккаті для регулятора та спостерігача).

2. Для фіксованої матриці K визначеної на попередньому етапі, вирішується задача мінімізації H_∞ – норми на всіх частотах при фіксованій матриці F_L(P,K).

. (15)

Як параметри оптимізації використовуються i – комплексних амплітуд при всіх фіксованих частотах , де k – індекс відповідної передатної функції в D(jω); ω_m – максимальна частота в смузі пропускання системи.

Після знаходження мінімуму (15) набор комплексних амплітуд апроксимується стійкими передатними функціями D_k, що входять в матрицю D*(jω). Далі обчислювалось структуроване сингулярне число μ.

Отриманий регулятор для процесу КМД задовольняє висунутим до нього вимогам, як частотному так і часовому просторі, за наявності достатньо високої параметричної невизначеності, що визначається у межах r_min ≤ r ≤ r_max та ε_min ≤ ε ≤ ε_max, та r_min, r_max, ε_min, ε_max – граничні значення термічного опору забруднень і поруватості мембрани. Регульованим параметром обрано перепад температур розчину та дистиляту на виході ММ.

ЛІТЕРАТУРА

1. Дубік Р.М. Математична модель розділення неоднорідних рідких систем. / Р.М. Дубік, Л.Р. Ладієва, // Автоматика. Автоматизация. Электротехнические комплексы и системы №1(23) – 2009 с. 49 – 54.

2. Ладієва Л.Р. Математичне моделювання процесу контактної мембранної дистиляції. / Л.Р. Ладієва, Р.М. Дубік // Хімічна інженерія, екологія та ресурсозбереження №2(6) – 2010 с. 119 – 122.

3. Дорф Р. Современные системы управления. / Р. Дорф, Р. Бишоп. Пер. с англ. Б.И. Копылова. – М.: Лаборатория Базовых Знаний, 2002. – 832 с.: ил.