УДК 669+54-142

О температурной зависимости ВЯЗКОСТи

жидкого натрия на основе

концепции хаотизированных частиц

А.Ш.Кажикенова, Д.Б. Алибиев

Карагандинский государственный университет им. Е.А.Букетова

Введение. Наиболее сложным для теоретического описания физико-химических свойств является жидкое состояние вещества. В структуре жидкости пространственное расположение атомов не закреплено, как в кристалле, но и не находятся в свободном состоянии, как в газе. Поэтому жидкость по своим свойствам может приближаться к газу вблизи температуры кипения или к твердому телу вблизи температуры плавления. Структуре жидкости характерен ближний порядок связи.

Основная характеристика жидкости – вязкость – не поддается строгому теоретическому выражению на основании различного учета сил связи частиц, то есть структурных факторов. Вязкость расплава имеет большую практическую важность в металлургии. В то же время, изучение вязкости металлических расплавов представляет значительный научный интерес, так как вязкость является наиболее структурно-чувствительной характеристикой расплава, дающей представление о внутренних силах взаимодействия частиц. Сотрудниками Химико-металлургического института (г. Караганда) была разработана модель температурной зависимости вязкости металлов, основанная на концепции хаотизированных частиц [1]. Согласно этому подходу, все три агрегатных вещества рассматриваются с единой точки зрения по его бесструктурной составляющей, которая численно определяется долей сверхбарьерных и подбарьерных по теплосодержанию в точках плавления RT_m и кипения RT_b частиц согласно распределению Больцмана.

Основная часть. Зависимость вязкости расплавов от температуры может быть выражена с точки зрения концепции хаотизированных частиц уравнениями [2], в которых учитывается определяющее тормозящее влияние на текучесть только кристаллоподвижных частиц

n , (1)

где n_r и T_r – соответственно кинематическая вязкость и абсолютная температура для некоторой реперной точки, выбираемой в принципе произвольно в качестве наиболее надежного экспериментального определения; либо ослабление этого влияния жидкоподвижными частицами

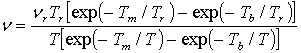, (2)

где T_m и T_b – соответственно температуры плавления и кипения; либо суммарное ослабление вязкости жидкоподвижными и пароподвижными частицами

n 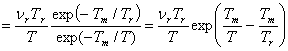. (3)

Широкая проверка этих трех моделей на всем доступном справочном материале по вязкости расплавов металлов показала [3], что, во-первых, не было ни одного случая неподчинения справочных данных какой-либо из трех предложенных моделей; во-вторых, эта подчиненность оказалась в согласии с различием в конфигурациях электронных оболочек и потенциалами ионизации металлов, т.е. с периодическим законом Д.И. Менделеева.

Но необходимость проверки каждой из трех моделей вязкости и выбора наиболее адекватной усложняет процедуру обработки данных. Это заставило нас более детально рассмотреть природу жидкого состояния вещества, оставаясь в рамках концепции хаотизированных частиц. Вероятно, более сильная зависимость от температуры помимо ее обоснования за счет разжижающего влияния жидкоподвижных и пароподвижных частиц может быть объяснена образованием ассоциированных или агрегированных элементарных кластеров, разрушение которых с повышением температуры происходит параллельно с разрушением элементарных кластеров, что и создает эффект более сильного влияния температуры на вязкость в случае формирования подобных ассоциатов или агрегатов. Это позволяет учесть данный эффект в рамках базовой модели (1) путем усиления фрагмента (Т_r/Т) так, как учитывается вероятность соударений одинаковых частиц (в данном случае кластеров), т.е. путем возведения вероятности элементарного события в степень, равную числу соударяющихся частиц:

n = n_r(T_r/T)^a. (4)

Здесь показатель a имеет смысл степени ассоциации`п-частичных кластеров. При а = 1 модель (4) сводится к модели (1). Проведенный анализ моделей (1), (2), (3) применительно ко всем расплавам металлов показал [3], что реальных зависимостей слабее (1) не обнаружено. Поэтому следует ожидать, что любая более сильная зависимость от температуры может быть выражена по (4) с а > 1.

Учет этого показателя хотя и потребует дополнительной обработки данных по вязкости, но зато позволит более детально отобразить структуру расплава с выходом на параметры, поддающиеся количественному выражению и физико-химическому контролю. Параметр а может быть определен из (4) путем логарифмирования

. (5)

Для определения а целесообразно использовать все экспериментальные значения вязкости при различных температурах за исключением n_r, T_r, приводящего к неопределенности а = 0/0, с последующим усреднением параметра агрегации:

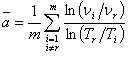. (6)

Как обычно, среднее значение необходимо проверить на представительность по критерию однородности множества и затем использовать в уравнении (4) для получения расчетных значений и сравнения с экспериментальными по коэффициенту корреляции.

Полученная обобщенная форма температурной зависимости вязкости может быть использована для расчета энергии активации вязкого течения расплава в комбинации с уравнением Френкеля, которое выведено для динамической вязкости

. (7)

Здесь А и U соответственно постоянные предэкспоненциальный множитель и энергия активации вязкого течения, смысл которых различными авторами трактуется в зависимости от предполагаемого характера межчастичного взаимодействия и квазикристаллической структуры жидкости [4].

Так как кинематическая вязкость связана с динамической вязкостью по формуле n = h/r (r - плотность расплава), то, ввиду весьма слабой зависимости плотности от температуры (несколько процентов во всем диапазоне жидкого состояния) в сравнении с 3-4 кратным изменением вязкости в том же диапазоне [4], можно напрямую заменить в уравнении (7) h на n, соответственно скорректировав параметры А и U на А^/ и Е_а. При этом энергия активации Е_а ввиду более сильной зависимости n от Т будет включать и небольшую часть (несколько процентов) по энергии разуплотнения расплава, в общем отличаясь от U в пределах точности эксперимента.

. (8)

Отмечается, что уравнение (7) справедливо для узкого диапазона температур и непригодно для полного описания жидкого состояния. Отсюда следует необходимость представления обобщенной зависимости (4) в координатах lnn-1/T для выделения псевдопрямолинейных участков с целью обработки их по модифицированному уравнению Френкеля (8) и определением величины энергии активации разуплотнения и вязкого течения. Возможно, это потребует пересчета исходных данных (при достаточности их объема) на этих участках с уточнением степени ассоциации кластеров на каждом их участков.

Необходимо отметить, что хотя выбор реперной точки не имеет принципиального значения, ее целесообразнее фиксировать вблизи (но не в самой точке) кристаллизации, так как при пониженных температурах вязкость определяется более надежно и имеет наиболее высокие значения. В самой же точке кристаллизации из-за возможного присутствия неопределенного количества равновесной твердой фазы вязкость эмульсии будет завышенной против вязкости чисто жидкого состояния.

Покажем применимость этих моделей на примере расплава натрия.

Для натрия известны температуры кипения и плавления: T_m=371К, T_b=1156,1 К. В [4] со ссылкой на работу [5] приводятся значения кинематической вязкости при различных температурах. Все имеющиеся данные сравнили с расчетными по моделям (1)-(4) с реперной точкой при температуре T_r = 400 К и n_r = 6,603×10^-7 м²/с (таблица 1 и рисунок 1). Независимо от выбранной реперной точки было установлено преимущество «второй» модели [3].

Среднее значение степени ассоциированности кластеров`а = 1,35. Однородность полученного множества для а по критерию Налимова соблюдается: S(x) = 0,123; = 1,808 < r_cr = 2,188.

Таблица 1 – Сопоставление экспериментальных данных [4] с рассчитанными по моделям (1)-(4) значениям кинематической вязкости натрия, n ×10⁷, м²/с

T	ν(эксп)	ν [4]	ν(1)	ν(2)	ν(3)	a	ν(4)
Tm = 371	9,685	7,853	7,119	7,481	7,654	-	7,310
400	6,603	6,874	6,603	6,603	6,603	-	6,603
450	5,493	-	5,869	5,514	5,295	1,563	5,632
500	4,728	4,857	5,282	4,762	4,388	1,497	4,885
550	4,171	-	4,802	4,217	3,729	1,442	4,295
600	3,752	3,830	4,402	3,806	3,231	1,394	3,818
650	3,426	-	4,063	3,487	2,844	1,351	3,427
700	3,137	3,224	3,773	3,232	2,536	1,330	3,101
750	2,956	-	3,522	3,026	2,284	1,279	2,825
800	2,783	2,832	3,302	2,855	2,076	1,246	2,589
850	2,64	-	3,107	2,711	1,902	1,216	2,385
900	2,517	2,562	2,935	2,589	1,753	1,189	2,208
1000	-	2,368	2,641	2,392	1,514	-	1,915
1100	-	2,226	2,401	2,242	1,331	-	1,684
Tb =1156,1	-	2,164	2,285	2,172	1,246	-	1,574
R	-	-	0,884	0,943	0,910	-	0,930

T_b

T,K

T_m

n×10⁷, м²/с

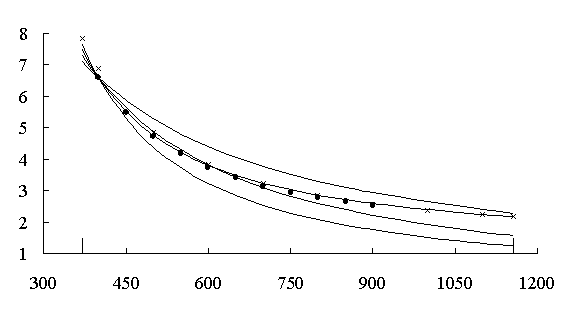
n - кинематическая вязкость, Т – температура.

Точки – экспериментальные данные [4],

1 – по первой модели , 2 – по второй, 3 – по третьей, 4 – по четвертой

Рисунок 1 – Зависимость кинематической вязкости натрия от температуры

Как видно из таблицы и рисунка, модели по (2) и обобщенная (4) являются более точными по описанию температурной зависимости.

Для этих моделей рассчитаны коэффициенты корреляции, которые соответственно равны 0,943 и 0,930. Значения коэффициентов корреляции почти равны между собой, поэтому для описания температурной зависимости достаточно применить модель более общего вида (4).

Таким образом, с учетом степени ассоциированности кластеров в качестве обобщенной модели вязкости расплавов в полном диапазоне температур можно использовать модель (4) с реперной точкой при T_r=400К и n_r = 6,603×10^-7 м²/с по кинематической вязкости меди с нахождением доверительного интервала и округлением

м²/с. (9)

Экспериментальные [4] и расчетные по обобщенной модели (4) данные для температурной зависимости кинематической вязкости обработали по модифицированному уравнению Френкеля (8). Их графическое изображение в координатах lnn-1/T показано на рисунке 2.

10⁴/T

lnν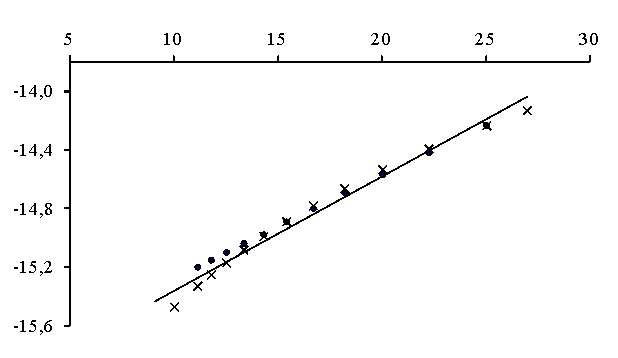

n - кинематическая вязкость, Т – температура.

Точки – усредненные экспериментальные данные,

крестики – для модели (4), прямая – по уравнению

Рисунок 2 – Зависимость логарифма кинематической вязкости натрия от обратной температуры

Вышеприведенные выкладки были проверены на 28 типичных металлах, для которых имеются справочные данные по вязкости. Во всех случаях обобщенная модель (4) описывает температурную зависимость вязкости более адекватно в сравнении с выбранной из ранее трех предлагаемых моделей, тем самым позволяя использовать модель более общего вида. В таблице 2 приведены значения степени ассоциации кластеров по уравнению (4) и энергии активации, полученные по модифицированному уравнению Френкеля на основе экспериментальных (справочных) и рассчитанных по обобщенной модели (4) данных для 28 металлов периодической системы Д.И. Менделеева.

Таблица 2 – Значения средней степени ассоциированности кластеров и энергии активации, рассчитанной по обобщенной модели (4) (Е_а(расч)) данных для 28 металлов

Элемент	`а	Еа(расч), Дж/моль	Элемент	`а	Еа(расч), Дж/моль
Li	1,04	6086	Rb	1,22	5055
Be	9,51	128017	Sr	2,01	22723
Na	1,35	6485	Ag	1,82	21684
Mg	2,57	22150	Cd	1,80	10867
Al	1,03	8871	In	0,96	5629
K	1,22	5878	Sn	0,97	5496
Ca	1,68	20171	Te	2,77	21476
Fe	3,54	55540	Cs	1,26	5313
Co	3,05	46835	Ba	1,56	17543
Ni	1,92	29757	Au	1,44	17294
Cu	1,65	22133	Hg	0,90	2868
Zn	1,90	14134	Tl	1,32	9154
Ga	0,91	4074	Pb	0,79	4714
Ge	2,81	31004	Bi	1,36	8447

Максимальное среднее значение степени ассоциированности кластеров у бериллия, наименьшие - у галлия, индия, олова, ртути и свинца. Практическое отсутствие ассоциации кластеров из атомов последних металлов является следствием ионной структуры расплавов металлов и практическим отсутствием в них молекулярных ковалентных связей. Особая вязкость расплава бериллия подробно обсуждается в статье [6] и связана с его высоким положением во второй группе таблицы Менделеева.

Выводы.

1. Создается возможность определить температурную зависимость вязкости на основе концепции хаотизированных частиц в полном диапазоне жидкого состояния на основе единой модели, учитывающей степень ассоциации элементарных кластеров из динамически существующих кристаллоподвижных частиц.

2. Полученная обобщенная форма температурной зависимости вязкости может быть использована для расчета энергии активации вязкого течения расплава в комбинации с уравнением Френкеля. Отсюда следует необходимость представления обобщенной зависимости в координатах lnn-1/T для выделения псевдопрямолинейных участков с целью обработки их по модифицированному уравнению Френкеля и определением величины энергии активации разуплотнения и вязкого течения.

Список литературы

1. Малышев В.П., Турдукожаева А.М., Кажикенова А.Ш. Вязкость расплавов металлов по концепции хаотизированных частиц // Тяжелое машиностроение. – 2009. – № 6. – С. 37-39.

2. Малышев В.П., Нурмагамбетова A.M. Зависимость вязкости расплавов от температуры на основе концепции хаотизированных частиц // Тез. докл. XV межд. конф. по хим. термодинамике в России, Москва, 2005. с. 197.

3. Турдукожаеелов,, ры МУндуковны Оч_________________________сотрудник (2004-2006 гг.), докторант ХМИ (200_________________________ва А.М. Применение распределения Больцмана и информационной энтропии Шеннона к анализу твердого, жидкого и газообразного состояний вещества (на примере металлов): автореф. дисс. … докт. техн. наук: 05.16.08. – Караганда: ХМИ, 2008. – 32 с.

4. Шпильрайн Э.Э., Фомин В.А., Сковородько С.Н., Сокол Т.Ф. Исследование вязкости жидких металлов. – М.: Наука, 1983. – 244 с.

5. Вертман А. А., Самарин А. М. Вязкость жидких сплавов меди и серебра // Изв. АН СССР. Металлургия и топливо, 1960. - № 4. – С. 95-98.

6. Милов И.В., Климов Ю.Ф., Скоров Д.М. О вязкости жидкого бериллия // Изв. АН СССР. Металлы, 1969. - № 4. – С. 82-83.