2 Механика

ГИРНИС С.Р., КОРНИЕНКО П.В., САКАНОВ К.Т.

Павлодарский государственный университет им. С. Торайгырова, Павлодар, Казахстан, e-mail:girnis@mail.ru.

Влияние скорости ДВИЖУЩЕЙСЯ В ЗАГЛУБЛЕННОМ ТОННЕЛЕ нагрузки на НАПРЯЖЕННО-деформированное состояние окружающего массива

Конструкции в виде замкнутых цилиндрических оболочек в упругой среде получили широкое применение в подземных сооружениях. Например, тоннельные обделки, капитальные горные выработки, трубопроводы и различные типы емкостей, находящиеся в грунте, можно свести к расчетной схеме оболочки на упругом основании. Вопросам исследования оболочек в упругой среде как пространственных систем посвящены работы [1, 2]. В этих работах описаны случаи статического нагружения. В статьях [3, 4] в точной и приближенной постановке решены задачи о воздействии стационарных осесимметричных подвижных нормальных нагрузок на оболочку в упругом пространстве. Численные исследования в [3, 4] ограничивались рассмотрением оболочки с фиксированным диаметром, что не позволяет судить о его влиянии на напряженно-деформированное состояние (НДС) окружающего массива. В настоящей работе, в отличие от [3, 4], равномерно движущаяся в осевом направлении по внутренней поверхности круговой цилиндрической тонкостенной оболочки нагрузка может иметь произвольный профиль, в частности может быть осесимметричной. Поскольку данная задача является модельной для тоннеля глубокого заложения (заглубленного тоннеля), полученное решение используется для численного исследования влияния скорости движущейся в тоннеле нагрузки на напряженно-деформированное состояние окружающего его породного массива. При этом радиус тоннеля варьируется.

1. В тех случаях, когда обделка кругового тоннеля глубокого заложения является тонкостенной конструкцией, в качестве расчётной модели можно принять расположенную в упругом пространстве тонкостенную оболочку с радиусом кривизны срединного слоя (рис.1). В силу малости толщины оболочки будем полагать, что окружающий массив контактирует с оболочкой вдоль её срединной поверхности. Контакт между оболочкой и окружающим её массивом будем полагать либо жёстким, либо скользящим.

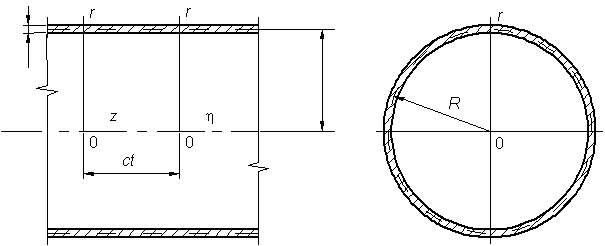
Рис. 1 – Тонкостенная оболочка в упругом пространстве

Пусть на внутреннюю поверхность оболочки действует нагрузка , движущаяся с постоянной дозвуковой скоростью в направлении оси .

Так как рассматривается установившийся процесс, то картина деформаций стационарна по отношению к движущейся нагрузке. Поэтому для решения задачи можно ввести подвижную цилиндрическую систему координат , связанную с нагрузкой.

Для описания движения оболочки воспользуемся классическими уравнениями теории тонких оболочек, которые в подвижной системе координат имеют вид [5]

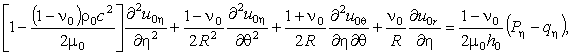
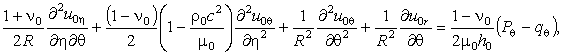(1)

.

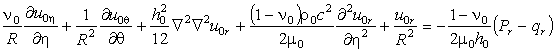где , , – перемещения точек срединной поверхности оболочки; , , – составляющие интенсивности подвижной нагрузки ; – составляющие реакции окружающей оболочку среды, – компоненты тензора напряжений в среде ; – соответственно коэффициент Пуассона, модуль сдвига и плотность материала оболочки; – оператор Лапласа.

Для описания движения массива используем динамические уравнения теории упругости в подвижной системе координат

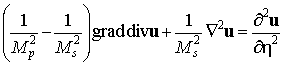. (2)

Здесь – вектор смещения упругой среды; – числа Маха; , – скорости распространения волн расширения – сжатия и сдвига в среде; ; , , – соответственно коэффициент Пуассона, модуль сдвига и плотность среды.

В случае жёсткого сцепления оболочки с окружающей средой

. (3)

При скользящем контакте и двухсторонней связи оболочки со средой

,

. (4)

Здесь – компоненты вектора u. Заметим, что при скользящем контакте в уравнениях (1) .

Задача сводится к совместному интегрированию уравнений движения оболочки (1) и массива (2) при выполнении граничных условий (3) или (4).

Выражая через потенциалы Ламе

, (5)

преобразуем уравнение (2) к виду

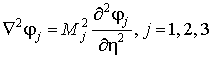, (6)

где .

Рассмотрим вначале подвижную нагрузку с произвольной зависимостью от угловой координаты и изменяющуюся вдоль синусоидально

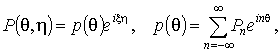
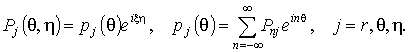(7)

Потенциалы также будем искать в виде периодических функций по

. (8)

Из (6) и (8) следует, что

(9)

Здесь , – двумерный оператор Лапласа.

Выразив компоненты напряженно-деформированного состояния среды через потенциалы Ламе можно получить выражения для перемещений и напряжений от синусоидальной нагрузки как функции от .

Так как скорость нагрузки меньше скорости распространения волн сдвига в среде, то и решения (9) можно представить в виде

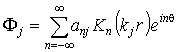, (10)

где – функции Макдональда, ; – неизвестные коэффициенты, подлежащие определению.

Подставляя (10) в выражения для и , получим новые выражения, где неизвестными будут только коэффициенты . Для определения последних, в зависимости от условия сопряжения оболочки со средой, воспользуемся граничными условиями (3) или (4), переписанными для и .

Для перемещений точек срединной поверхности оболочки при действии синусоидальной нагрузки, имеем

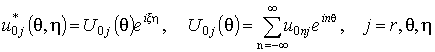. (11)

Подставляя (7) и (11) в уравнения (1), для n-го члена разложения получим

(12)

,

где

,

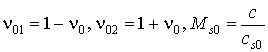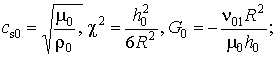
при r = R: , , – в случае жесткого контакта; , , – в случае скользящего контакта.

Разрешая (12) относительно , , , находим

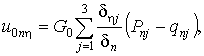
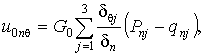(13)

.

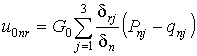Здесь

;

для и индекс j = 1 соответствует индексу , j = 2 – , j = 3 – r.

Подставляя (13), в зависимости от типа контакта, в (3) или (4) и приравнивая коэффициенты рядов Фурье-Бесселя при , получим бесконечную систему линейных алгебраических уравнений блочно-диагонального вида для определения коэффициентов , решение которой находим известным методом, если соответствующий для каждого n определитель системы отличен от нуля.

Зная решение задачи для синусоидальной нагрузки, реакцию упругого пространства на движущуюся апериодическую нагрузку характерного для транспортируемых объектов типа формально получаем при помощи суперпозиции, используя представление нагрузки и компонент НДС среды в виде интегралов Фурье:

,;

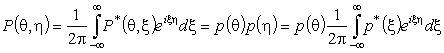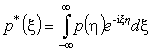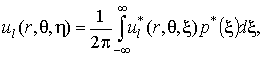
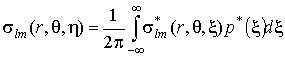. (14)

Окончательное решение будет зависеть от конкретного вида движущейся нагрузки.

Для вычисления интегралов (14) можно использовать любой численный метод, если скорость движения нагрузки меньше её критических скоростей, значения которых определяются при исследовании определителей разрешающей системы уравнений. Приравнивая симметричные относительно n и функции к нулю можно получить численными методами дисперсионные кривые в плоскости . Для фиксированного значения n координатам любой точки кривой соответствует свободная волна, распространяющаяся вдоль оси оболочки. Форма этой волны зависит от числа n и удовлетворяет соответствующей однородной системе уравнений. Проведенные численные исследования показали, что в зависимости от физико-механических и геометрических параметров задачи, для каждой n-моды может существовать дозвуковая, соответствующая минимуму построенной в плоскости дисперсионной кривой критическая скорость , при которой в двух точках

.

В этом случае стационарного решения задачи для данной моды не существует. Причём, минимальная критическая скорость, независимо от условия сопряжения оболочки со средой, имеет место при n = 0. Поэтому, если , то для любых и n, и для вычисления интегралов (14) можно воспользоваться численными методами.

При для каждого n существуют четыре особые точки , в которых

.

В этих случаях решение существует, если ранг расширенной матрицы равен рангу матрицы системы уравнений для данной n-моды. Как показано в [6], при движении с такими сверхкритическими скоростями нагрузка генерирует позади себя свободные цилиндрические незатухающие вдоль оси оболочки гармонические волны частоты и длины , движущиеся вдоль поверхности оболочки вслед за действующей нагрузкой с той же скоростью. Амплитуда этих волн не зависит от z и экспоненциально затухает при .

При точки и сливаются в одну . Стационарного решения задачи в этом случае не существует. Для таких скоростей в оболочке возникают резонансные явления, для изучения которых следует переходить к нестационарной постановке задачи. Значение параметра задачи можно характеризовать как точку бифуркации решения, при переходе через которую возникает неустойчивость движения. Этот факт может оказаться существенным для практики строительства подземных транспортных сооружений.

2. В качестве примера рассмотрим тоннель глубокого заложения в породах различной жёсткости:

- в известняке (= 0,25, МПа, кг/м³; = 1028м/с);

- в песчанике (= 0,28, МПа, кг/м³; = 1766м/с).

Определим толщину динамически активного слоя массива вокруг тоннеля радиусом R, подкреплённого стальной ( = 0,3, МПа, кг/м³) оболочкой (обделкой) толщиной  = 0,01м. В таблицах 1, 2 помещены результаты расчёта деформированного состояния породных массивов в поперечном сечении тоннеля h = 0 для случая скользящего контакта обделки с массивом. Расчёты проводились для разных радиусов тоннеля и скоростей движения рассматриваемой здесь нагрузки.

Таблица 1 – Радиальные перемещения u^°_r = u_rm/P^° точек массива в поперечном сечении тоннеля h = 0 при c = 200 м/с.

Породный массив	R = 1м				R = 3м
	r/R				r/R
	1,0	2,0	3,0	4,0	1,0	2,0	3,0	4,0
	u^°r, м				u^°r, м
известняк	0,175	0,035	0,015	0,008	0,295	0,042	0,018	0,010
песчаник	0,189	0,040	0,017	0,009	0,292	0,044	0,019	0,010

Таблица 2 – Радиальные перемещения u^°_r = u_rm/P^° точек массива в поперечном сечении тоннеля h = 0 при c = 800 м/с.

Породный массив	R = 1м				R = 3м
	r/R				r/R
	1,0	2,0	3,0	4,0	1,0	2,0	3,0	4,0
	u^°r, м				u^°r, м
известняк	0,274	0,064	0,025	0,013	0,544	0,077	0,031	0,017
песчаник	0,210	0,046	0,020	0,010	0,332	0,050	0,021	0,012

Из таблиц следует, что повышение скорости нагрузки в 4 раза ведёт к возрастанию прогибов тоннеля: в известняке при R = 1 м и R = 3 м соответственно в 1,6 и 1,8 раз; в песчанике при R = 1 м и R = 3 м – приблизительно в 1,1 раза. Таким образом, увеличение скорости нагрузки оказывает более значительное влияние на деформированное состояние поверхности того тоннеля, который проходит в менее жёстком породном массиве. Во всех случаях с удалением от поверхности тоннеля значения радиальных перемещений точек массива быстро затухают и при r/R = 4,0 становятся намного меньше (менее 5%) перемещений контура поперечного сечения тоннеля (r/R = 1,0). Поэтому толщина динамически активного слоя породного массива вокруг тоннеля при любой скорости нагрузки равна трём его радиусам, если допускаемая погрешность по критерию перемещений поверхности тоннеля составляет 5%. Следовательно, любой тоннель при r/R ³ 4,0 можно считать тоннелем глубокого заложения, так как в этом случае воздействие на массив отраженных от земной поверхности волн будет пренебрежительно мало. Кривые изменений компонент напряжённо-деформированного состояния массива песчаника с удалением от поверхности тоннеля радиусом R = 3 м при скорости движения нагрузки c = 800 м/с представлены на рис. 2 – 4.

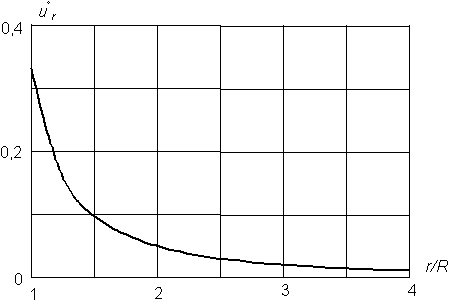
Рис. 2 – Изменение радиальных перемещений u^°_r, м в массиве

песчаника с удалением от поверхности тоннеля радиусом R = 3 м

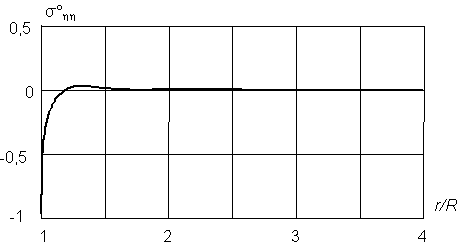
Рис. 3 – Изменение нормальных напряжений s^°_hh в массиве

песчаника с удалением от поверхности тоннеля радиусом R = 3 м

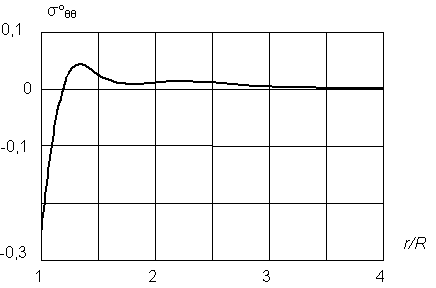
Рис. 4 – Изменение нормальных напряжений s^°_θθ в массиве

песчаника с удалением от поверхности тоннеля радиусом R = 3 м

Литература:

1 Баженов В.А. Изгиб цилиндрических оболочек в упругой среде. - Львов. 1975. 264 с.

2 Булычев Н.С. Механика подземных сооружений в примерах и задачах. – М.: Недра, 1989. – 270 с.

3 Львовский В.М., Онищенко В.И., Пожуев В.И. Установившиеся колебания цилиндричес-кой оболочки в упругой среде под действием подвижной нагрузки //Сб.: Вопросы прочности пластичности. – Днепропетровск, 1974. – С. 98-110.

4 Пожуев В.И., Львовский В.М. Реакция цилиндрической оболочки в упругой среде на действие подвижной нагрузки // Изв. вузов. Строительство и архитектура. – 1976. – № 2. – С. 61-66.

5 Вольмир А.С. Нелинейная динамика пластин и оболочек. – М.: Наука, 1972. – 432 с.

6 Ержанов Ж.С., Айталиев Ш.М., Алексеева Л.А. Динамика тоннелей и подземных трубопроводов. – Алма-Ата: Наука, 1989. – 240 с.