УДК 631.312.62

РАЗРАБОТКА КОНСТРУКЦИИ универсального КОПАЧА КОРНЕПЛОДОВ ТИПА «СКОБА»

Сокол С.П., Кобец А.С., Науменко Н.Н.

Днепропетровский государственный аграрный университет,

г. Днепропетровск, Украина

Предложена математическая модель для определения сопротивления передвижения скобы в почве. Выяснены зависимости сопротивления от скорости движения скобы и ее геометрических характеристик. Установлен угол наклона клина, при котором сопротивление его передвижению в почве минимально. Обоснована форма стоек скобы.

Наиболее характерной тенденцией влияющей на совершенствование выкапывающих рабочих органов является интенсификация процесса выкапывания, заключающаяся в ограничении количества поступающей в машину почвы и повышении интенсивности ее деформации. Такие требования к уборке урожая приводят к необходимости разрабатывать рабочие органы, обеспечивающие минимальные потери и повреждения корнеплодов с различными физико-механическими характеристиками при их выкапывании. В качестве нового рабочего органа предлагается копач типа «скоба» [1, 2] у которого конструктивными основными элементами являются подрезающий двугранный клин (лемех) и несущие и одновременно режущие стойки-ножи (рис. 1). В процессе работы скоба сжимает слой почвы, который как демпфер мягко передает давление на корнеплод, разрывая при этом наложенные на него связи. Пройдя сквозь скобу, разрушенный слой почвы обрушивается на прежнее место, а высвобожденный корнеплод остается на поверхности.

Постановка проблемы. Так как основным рабочим элементом копача корнеплодов типа «скоба» есть лемех, то он в значительной степени будет определять сопротивление передвижению рабочего органа в почве. Определение оптимального угла наклона лемеха, а также анализ его взаимодействия с почвой является чрезвычайно важной задачей, решение которой желательно иметь уже на стадии проектирования рабочего органа.

Анализ последних исследований. Динамика перемещения пласта почвы по поверхности двугранного клина была рассмотрена доктором технических наук Г.Н. Синеоковым [15]. Им была получена аналитическая зависимость для определения максимально допустимой длины лемеха, при котором перемещения почвы будет переходить без сгруживания. Теоретические исследования в этом направлении, которые рассматриваются в литературе [3, 5–9], не дают рекомендаций по расчету сопротивления перемещению любого рабочего органа, а формулы, которые предлагаются, применимы только в отдельных конкретных случаях. Например, коэффициенты известной формулы для расчета силы тяги плуга определяются по опытным данным для ряда плугов различных марок уже существующих [6]. Совершенно очевидно, что возможны трудности при применении этой рациональной формулы для проектирования рабочих органов сельскохозяйственных машин, конструктивно отличающихся от плуга.

а б

в г

Рисунок 1 – Фрагменты полевых и лабораторных исследований скобы:

а, б – выкопка корнеплодов моркови и сахарной свеклы; в – модель скобы в почвенном канале; г – рабочий момент взаимодействия модели с почвой

Промышленностью сегодня выпускается достаточно широкий перечень рабочих органов, которые используются как для обработки почвы, так и для выкапывания корнеплодов. В большинстве случаев основной частью рабочего органа является клин или поверхность рабочего органа можно представить как набор отдельных плоских элементов, т.е. клиньев. Следовательно, определение сопротивления передвижению рабочего органа можно свести к вычислению сопротивления одного клина (например, лемеха) или нескольких клиньев вместе, которыми можно представить более сложную поверхность (например, криволинейная стойка скобы или стрельчатая лапа культиватора).

Целью исследований является определение аналитических зависимостей сопротивления перемещению клина от основных характеристик и параметров системы «клин-почва» на основании данных анализа взаимодействия двугранного клина с почвой, а также обоснование рекомендаций по выбору угла наклона клина и конструкции скобы в целом.

Результаты исследований. При проведении лабораторных и полевых испытаний с рабочим органом типа «скоба» (рис. 1,а) наблюдениями за процессом взаимодействия рабочего органа с почвой обнаружено, что при подрезании поверхностного слоя нижней режущей плоской частью скобы почва разрушается не непрерывно, а разламывается на отдельные объемы, что зафиксировано на (рис. 1,б). Можно предположить, что отдельный объем почвы сначала уплотняется под давлением плоской нижней части скобы – лемехом, а затем откалывается от монолитной части поверхностного слоя почвы. Эти наблюдения позволили взять за расчетную модель взаимодействия клина с почвой схему, предложенную академиком В.П. Горячкином [6].

При подрезании поверхностного слоя почвы лемехом элементы почвы 1, 2, 3, которые взаимодействуют с ним (рис. 2), образуются из материала, имеющего в вертикальном сечении начальную форму параллелограмма . Горизонтальное перемещение клина по линии сопровождается смятием и крошением почвы в объеме, обозначенном параллелограммом , который впоследствии деформируясь, принимает форму и занимает место первого элемента на клине.

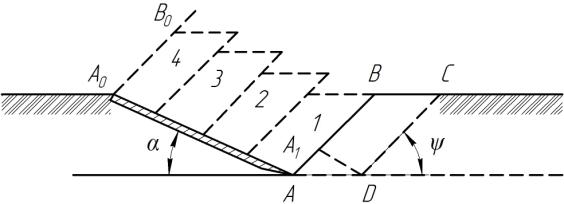
Рисунок 2 – Схема движения почвы по поверхности лемеха

В дальнейшем почва рассматривается как сплошная среда, что может быть целесообразным для определения сопротивления перемещения клина в ней [4]. К анализу движения объема почвы, находящегося на расчетной схеме, в объеме, ограниченном ломаной (рис. 3), используется теорема Эйлера для сплошной среды [10], которая для относительного движения почвы по клину в рассматриваемом случае будет иметь вид:

    (1)

В векторном уравнении (1) введены обозначения: – секундное количество движения почвы, проходящей через сечение в относительном движении; – секундное количество движения почвы, проходящей через сечение ; _, – главные векторы поверхностных сил, соответственно нормальных и сил трения на клине; – масса объема почвы на клине; – сила скалывания, которая возникает на границе рассматриваемого объема почвы; – нормальная реакция на линии скалывания.

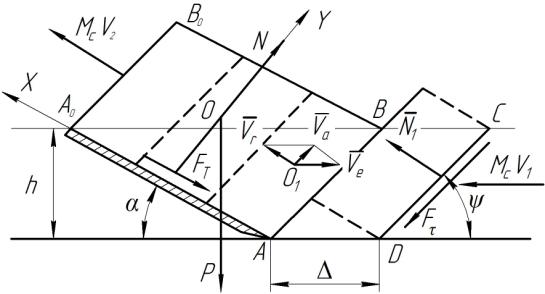
Рисунок 3 – Схема к математической модели взаимодействия почвы с клином

Считается, что скалывание почвы при перемещении клина происходит по линии составляющей с горизонтом некоторый угол , который может быть определен как [6]:

где – углы наклона лемеха, трения почвы на нем и внутреннего трения почвы соответственно.

Сила скалывания действует на линии сдвига и определяется формулой:

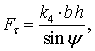
где и – соответственно ширина лемеха, и глубина его хода; – предельное сопротивление чистого сдвига для почвы; – угол скалывания.

Проектируя вектор уравнения (1) на ось получим выражение:

Откуда для силы нормального взаимодействия почвы с клином можно получить выражение:

(2)

Считая, что сила трения пропорциональна нормальной реакции, получим:

(3)

где – коэффициент трения между материалом клина и почвой.

Проектируя уравнение (1) на направление относительного движения, вдоль клина, получим:

откуда

(4)

В дальнейшем примем, что секундные массы на «входе» в исследуемый объем почвы и на «выходе» из него равны между собой, то есть:

Кроме этого, заметим, что относительная скорость на входе равна скорости клина , т.е. и секундную массу в дальнейшем будем определять как

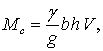(5)

где – удельный вес почвы.

Для определения относительной скорости обратим внимание на то, что абсолютное перемещение почвы на клине осуществляется параллельно линии скалывания. Из параллелограмма скоростей (рис. 4), получим 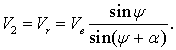На основании изложенного, вместо выражения (4) придем к:

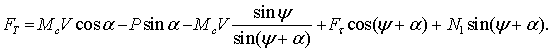(6)

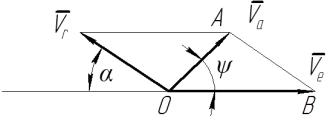
Рисунок 4 – Схема к определению скорости

Из формул (3) и (6), учитывая выражение (5), можно получить:

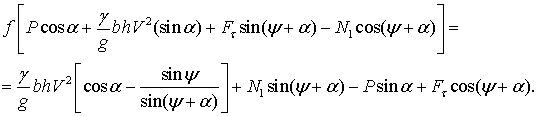
Тогда

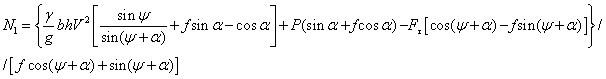(7)

С определением силы выражения (2) и (6) позволяют устанавливать силы взаимодействия клина с почвой. Рабочее сопротивление перемещению клина можно рассчитать, проектируя силы и на направление движения рабочего органа:

(8)

Как видно из приведенных зависимостей, сопротивление перемещению клина при известных механических характеристик системы «клин-почва» определяется его размерами, скоростью перемещения и углом наклона к горизонту. В качестве примера проведено исследование зависимости сопротивления перемещению клина от угла его наклона при таких исходных данных: ширина клина м; глубина хода м, скорость движения м/c; угол трения рад.; Угол внутреннего трения рад.; предельное сопротивление Па.

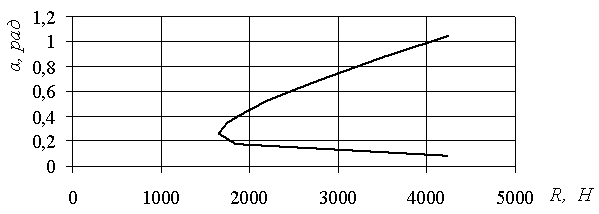
Рисунок 5 – Зависимость сопротивления от угла наклона лемеха

По приведенной на рис. 5 зависимости сопротивления перемещению при принятых исходных данных минимальное сопротивление составляет 1644,98 Н. Как показывают расчеты, при варьировании геометрических характеристик клина и механических характеристик системы «клин-почва» минимальное сопротивление всегда реализуется в диапазоне изменения угла 15⁰...20⁰.

Относительно проектирования формы и ориентировки в пространстве стоек скобы принята во внимание информация В.И. Ветохина [11]. Предполагается и подтверждается исследованиями, что при движении лемеха в почве на его поверхности образовывается тело из уплотненной почвы. Это зона, в которой почва находится в пластическом состоянии, она ограничена полусферической поверхностью, и давление от нее передается гидростатическое, то есть равномерное во все стороны (рис. 6.). На основании вышеизложенного можно сделать вывод, что в том случае, когда стойки скобы принимаются вертикальными и плоскими, почва в зоне пластичности будет создавать давление на каждую стойку и сопротивление передвижению скобы существенно увеличится. Для того чтобы при проектировании скобы этого избежать, для этого предлагается лемех на участке (рис. 7), который определяется скалыванием почвы не ограничивать стойками скобы [13, 14]. Очевидно, что для участка клина, часть которого выходит за границы скобы, лобовое скалывание по линии (рис. 7) сопровождается еще и боковым скалыванием по линиям 1 и 2 (рис.6).

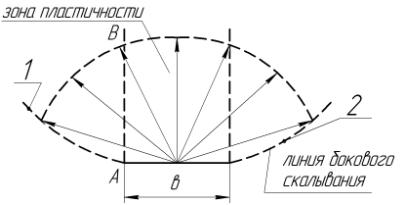
Рисунок 6 – Схема зоны уплотнения и боковых поверхностей линий скалывания почвы

В связи с этим в вертикальном поперечном сечении скобы профиль каждой стойки-ножа в нижней части должен совпадать с линией бокового скалывания или быть максимально приближен к ней. В верхней части линия сечения стойки принимается прямолинейной и параллельной профилю корнеплода (для свеклы угол (рис. 7) принимается равным 15^о). В нижней части, линия сечения очевидно должна быть криволинейной и желательно, чтобы касательная к ней в нижней точке совпадала с горизонтальной линией сечения клина. За исходные данные при проектировании скобы принята, как известная, высота рабочей части , которая определяется агрофизическим характеристиками корнеплода. На основании статистических данных для свеклы принято м. Конструктивно принят поперечный размер рабочей части скобы м, (рис. 7).

На основе существующих рекомендаций для углов резания почвы клином, а также на основании анализа, проведенного в данной статье, угол наклона клина принимается равным 20^о. Длина клина принимается такой, чтобы обеспечить необходимое значение вертикального перемещения корнеплода на дневную поверхность. Будем считать достаточным вертикальное перемещение корнеплода на половину его длины, то есть:

м.

Тогда общая длина лемеха скобы:

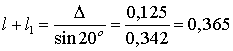м.

Окончательно примем м, что обеспечивает не повреждение корнеплода в связи с подрезанием почвы клином ниже слоя, в котором он находится. Длина участка клина определяется процессом уплотнения грунта во время горизонтального перемещения клина до момента скалывания почвы. Очевидно, что эта длина ( на рис. 7) для различных почв может существенно меняться. В процессе разработки конструкции скобы этот размер варьировался и за удовлетворительное значение для выкапывания свеклы на супесчаных почвах принято м.

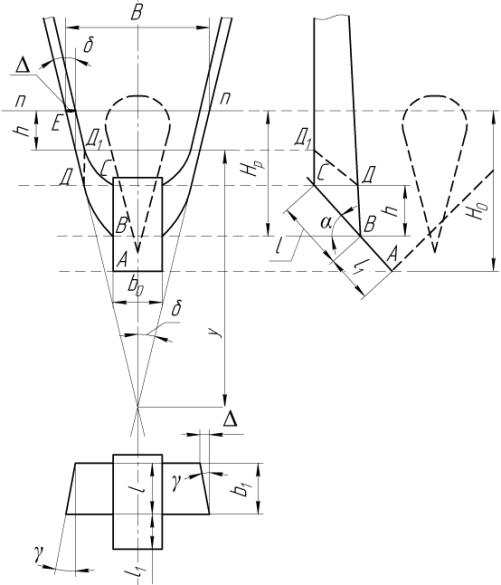
Рисунок 7 – Схема к проектированию криволинейной, развёртывающейся поверхности стоек скобы

В поперечном вертикальном сечении стойкам скобы в ее рабочей части придано форму гиперболы, ветви которой разведены от оси симметрии на ширину клина . Параметры гиперболы, уравнение которой в системе координат (рис. 8) имеет вид:

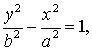(9)

определяются из того условия, что каждая асимптота должна составлять с осью гиперболы угол , для которого принято значение 15^о.

Из этого следует, что то есть

Определив высоту рабочей части стойки скобы, как и подставив координаты крайней верхней точки этой части и в уравнение (9), можно определить параметры гиперболы «» и «». При принятых ранее геометрических размерах см, см и см для параметров «» и «» получено см, а=3,37 см. Таким образом, линия вертикального поперечного сечения стоек стойки описывается уравнением:

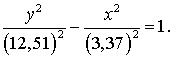
Две ветви этой гиперболы вместе с клином, на ширину которого они разведены от оси симметрии, образуют вертикальный профиль скобы, а боковая поверхность скобы образуется перемещением полученного профиля вдоль клина.

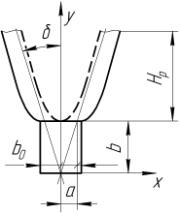
Рисунок 8 – Схема к определению контура вертикального сечения скобы

По завершению скалывания уплотненный снизу массив почвы, двигаясь вдоль клина, поступает в пространство, находящееся между двумя стойками. После скалывания нагрузки массива от напряжений, возникающих на поверхностях скалывания, исчезает, однако корнеплод остается в массиве почвы и необходимо создать условия для его освобождения и вынос на дневную поверхность. С этой целью предполагается сужение пространства между двумя стойками скобы. Сужение обеспечивается разворотом стоек скобы на некоторый угол атаки вокруг оси, перпендикулярной плоскости клина (рис. 9а). Как показали расчеты, достаточным для обеспечивания разрушения потока почвы между стенками стоек является значение . На основании изложенного предложено три конструктивных варианты скобы [12–14]: скоба с симметричным сечением (рис. 9а); скоба с минимальным перекрытием (рис. 9б); скоба без зоны перекрытия (рис. 9в). Скобу симметричную можно рекомендовать для работы на песчаных почвах.

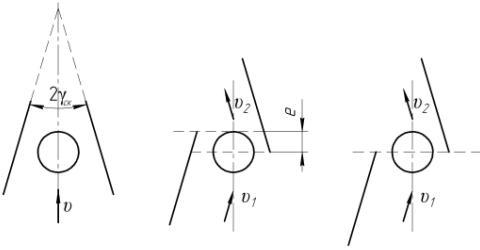
а б в

Рисунок 9 – Варианты смещения стоек-ножей скобы в горизонтальном направлении: а – с образованием зоны перекрытия; б – с образованием минимального зоны перекрытия; в – без образования зоны перекрытия

Скобу с незначительной зоной перекрытия (принимается, что ширина (рис. 9б) равна половине диаметра корнеплода в среднем по его длине сечении) можно рекомендовать для работы в более плотной почве в связи с тем, что сопротивление перемещению такой скобы будет значительно меньше. Скобу без зоны перекрытия можно считать универсальной и выгодной при работе на уплотненных почвах в связи с тем, что разрушение почвы стойки-ножи обеспечивают не сжатием потока, а его изгибом в горизонтальной плоскости, вызванным изменением направления движения, что, безусловно, требует значительно меньших энергетических затрат.

Выводы

1. На основе лабораторных исследований и анализа относительного движения почвы по поверхности скобы разработана математическая модель динамического взаимодействия клина с почвой.

2. Определена возможность устанавливать сопротивление перемещению клина в почве при равномерном прямолинейном движении по заданным характеристикам клина и почвы.

3. На основании проведенных исследований предлагается устанавливать угол наклона лемеха скобы в диапазоне 15⁰...20⁰.

4. Обоснована форма стоек и предложено три варианты конструкции скобы.

_{Список использованной литературы:}

1. Пат. № 43775 Україна, МПК А 01D 25/04. Викопувальний орган коренезбиральної машини / Кобець А.С., Сокол С.П., Науменко М.М., Кобець О.М., Волик Б.А., Пугач А.М.; Дніпропетровський ДАУ. – № u2009 04143; заявл. 27.04.2009; опубл. 25.08.2009, Бюл. № 16.

2. Пат. № 49323 Україна, МПК А 01D 25/00. Викопувальний орган коренезбиральної машини / Кобець А.С., Сокол С.П., Науменко М.М., Кобець О.М., Волик Б.А., Пугач А.М.; Дніпропетровський ДАУ. – № u2009 11390; заявл. 09.11.2009; опубл. 26.04.2010, Бюл. № 8.

3. Аронин Е.Д. Метод определения коэффициентов рациональной формулы В.П. Горячкина / Е.Д. Аронин // Механизация и электрификация сельского хозяйства. – 1982. – № 4. –С. 42–44.

4. Василенко П.М. Математические модели почв, как сплошных сред / П.М. Василенко // Научные труды УСХА. –1978. – Вып. 198. –С. 3–6.

5. Вилде А.А. Влияние конструктивных параметров лемешно-отвальной поверхности и корпуса плуга на их тяговое сопротивление / А.А. Вилде // Механизация и электрификация сельского хозяйства. – Рига, 1983. – Вып. 8 (15), № 4. –С. 203–230.

6. Горячкин В.П. Собрание сочинений: Т. 2. – Изд. 2-е; под ред. Н.Д. Лучинского. / В.П. Горячкин //– М.: Колос, 1968. – 455 с.

7. Дьяков В.П. Об анормальных отклонениях формулы Горячкина / В.П. Дьяков // Техника в сельском хозяйстве. – 1989. – № 1. –С. 10–12.

8. Сергеев М.П. О физической сущности составляющих рациональной формулы В.П. Горячкина / М.П. Сергеев // Труды ЧИМЭСХ. – Челябинск, 1970. – Вып. 43, ч. 1. –С. 18–21.

9. Игамбердиев И.Х. Приведенное тяговое сопротивление плуга / И.Х. Игамбердиев // Механизация и электрификация сельского хозяйства. – 1981. – № 7. –С. 53–54.

10. Яблонский А.А. Курс теоретической механики, ч.2. / А.А. Яблонский. – М.: Высшая школа, 1977. Ч. 2. – 531 с.

11. Ветохин В.И. К теории почвообрабатывающего клина / В.И. Ветохин // Загальнодержавний міжвідомчий науково-технічний збірник. Конструювання, виробництво та експлуатація сільськогосподарських машин, вип. 41, ч. 1. – Кіровоград: КНТУ, 2011. – С. 301 – 308.

12. Пат. № 43775 Україна, МПК А 01D 25/04. Викопувальний орган коренезбиральної машини / Кобець А.С., Сокол С.П., Науменко М.М., Кобець О.М., Волик Б.А.; Дніпропетровський ДАУ. – № u2009 04143; заявл. 27.04.2009; опубл. 25.08.2009, Бюл. № 16.

13. Пат. № 55485 Україна, МПК А 01D 25/00. Викопувальний орган коренезбиральної машини / Кобець А.С., Науменко М.М., Сокол С.П., Кобець О.М., Пугач А.М.; Дніпропетровський ДАУ. – № u2010 08528; заявл. 08.07.2010; опубл. 10.12.2010, Бюл. № 23.

14. Пат. № 56761 Україна, МПК А 01D 25/00. Викопувальний орган коренезбиральної машини / Кобець А.С., Науменко М.М., Сокол С.П., Кобець О.М., Пугач А.М.; Дніпропетровський ДАУ. – № u2010 08558; заявл. 08.07.2010; опубл. 25.01.2011, Бюл. № 2.

15. Синеоков Г.Н. Теория и расчет почвообрабатывающих машин / Г.Н. Синеоков, И.М. Панов – М.: Машиностроение, 1977. – 327 с.