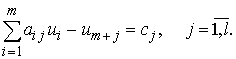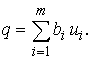ТЕНЕВЫЕ ЦЕНЫ ПРИ РАСПРЕДЕЛЕНИИ РЕСУРСОВ

Пчелинцев И.А, Гарькина И.А.

Пензенский государственный университет архитектуры и строительства

Наибольшую ценность обычно имеют те ресурсы, которые в наибольшей степени ограничивают выпуск продукции [1], тем самым и доход предприятия. Поэтому предприятие, очевидно, будет готово увеличивать именно эти ресурсы, несмотря на возможные значительные расходы. Отсюда следует, что каждый вид ресурса обладает некоторой теневой ценой, определяющей ценность ресурса для предприятия, то есть для дохода от реализации выпускаемой продукции, зависящей от наличного запаса этого ресурса и потребности в нем для выпуска продукции. Чем более ограничен ресурс, и чем больше потребность в нем при выпуске продукции, тем теневая цена этого ресурса будет выше. Однако установленные при принятом на предприятии технологическом процессе теневые цены не обязательно будут наилучшими. Введение других технологических процессов, возможно, позволит более рационально использовать все запасы ресурсов. Таким образом, существуют оптимальные теневые цены, соответствующие максимальному доходу предприятия, то есть оптимальному распределению ресурсов.

Как видим, определение оптимальных теневых цен оказывается тесно связанным с задачей линейного программирования, описываемой системой

a₁₁ x₁ + a₁₂ x₂ + ...+ a_{1 n} x_n = b₁ ,

a₂₁ x₁ + a₂₂ x₂ + ... + a_{2 n} x_n = b₂ ,

… (1)

a_m1 x₁ + a_m2 x₂ + ...+ a_{m n} x_n = b_m ,

b_i ³ 0, i = ,

и целевой функцией

f = c₁ x₁ + c₂ x₂ + ... + c_n x_n . (2)

Для определения оптимальных теневых цен возможно составление и самостоятельной задачи линейного программирования. Действительно, обозначим теневую цену единицы ресурса S_i через u_i . Значения u_i должны быть такими, чтобы теневая цена ресурсов, используемых в любом технологическом процессе, не была меньше получаемого дохода

Если ввести переменные u_{m+ j} ³ 0, представляющие собой превышение теневой цены единицы продукции над доходами от её реализации, то эта система неравенств превратится в систему уравнений:

(3)

Оптимальными ценами будут те, которые минимизируют общую стоимость ресурсов

(4)

Система ограничений (3) совместно с целевой функцией (2) даёт новую задачу линейного программирования, называемую двойственной задачей по отношению к прямой, или основной задаче линейного программирования, определяемой уравнениями (1) и (2). Прямая и двойственная задачи тесно связаны между собой. Если прямая задача является задачей максимизации, то двойственная - задачей минимизации.

Коэффициенты c_j целевой функции f в прямой задаче являются свободными членами ограничений двойственной задачи. Свободные члены b_i из ограничений прямой задачи становятся коэффициентами целевой функции q в двойственной задаче. Коэффициенты a_ij при переменных u_i в ограничениях двойственной задачи представляют собой столбцы матрицы прямой задачи. Знаки неравенств в ограничениях меняются на противоположные.

По первой теореме двойственности если одна из пары двойственных задач имеет оптимальный план, то и другая имеет оптимальный план и значения целевых функций задач при их оптимальных планах равны между собой, то есть f_max = q_min .

Проиллюстрируем интерпретацию двойственной задачи на простом примере. Пусть диета должна обеспечивать не менее четырёх единиц протеина (фунт арахисового масла даёт единицу протеина, фунт бифштекса - две единицы). Определить оптимальную диету, минимизирующую стоимость всей диеты, если фунт арахисового масла стоит 2 доллара, а фунт бифштекса - 3 доллара. Для диеты, содержащей x₁ фунтов арахисового масла и x₂ фунтов бифштекса x₁ + 2 x₂ ³ 4, x₁ ³ 0, x₂ ³ 0. Стоимость всей диеты f = 2x₁ + 3x₂; оптимальная диета: x₁^* = 0, x₂^* = 2; f_max = 6 долларов.

Для покупателя, выбирающего между бифштексом и арахисовым маслом из условия минимальной стоимости получаемого протеина, двойственной задачей является та, которая стоит перед продавцом, продающим синтетический протеин (конкуренция между бифштексом и арахисовым маслом). Аптекарь хочет максимизировать цену синтетического протеина u₁ . Она подчиняется линейным ограничениям. Во-первых, синтетический протеин не должен стоить больше, чем протеин в арахисовом масле (2 доллара за единицу) или в бифштексе (3 доллара за две единицы). При этом цена u₁ должна быть не отрицательной. Поскольку диета требует четыре единицы протеина, доход продавца будет q = 4 u₁ . Возникает двойственная задача: максимизировать q = 4 u₁ , если u₁ £ 2, 2 u₁ £ 3 и u₁ ³ 0. Здесь двойственную задачу решить легче, чем исходную (она имеет лишь одну неизвестную u₁). Ясно, что фактически действует лишь одно ограничение 2 u₁ £ 3 и максимальная цена u₁ синтетического протеина равна 1,5 доллара. Поэтому максимальный доход q_max = 6 долларов. Это была минимальная стоимость в исходной задаче, и покупатель платит одинаково как за натуральный, так и за синтетический протеин. В этом и состоит смысл теоремы двойственности.

Приведенный подход эффективно использовался при выборе модификаторов для композиционных строительных материалов.

Литература

1. Данилов А.М.,Гарькина И.А., Домке Э.Р. Математическое и компьютерное моделирование сложных систем. - Пенза: ПГУАС, 2011. -296 с.