К.т.н. Маслій Р.В., Філіпчук О.Ю.

Вінницький національний технічний університет

ЗАСТОСУВАННЯ ВИПАДКОВИХ ЛІСІВ ДЛЯ КЛАСИФІКАЦІЇ ДАНИХ

Дерево рішень – це один з методів автоматичного аналізу великих масивів даних. Ідея, яка лежить в основі методу дерева рішень, полягає у розбитті множин можливих значень вектора ознак (незалежних змінних) на множини, які не перетинаються і підгонці простої моделі для кожної такої множини. Отже, мета цього методу полягає в тому, щоб створити модель, яка прогнозує значення цільової змінної на основі декількох змінних на вході.

Області використання метода дерева рішень наступні:

· опис даних: дерева рішень дозволяють зберігати інформацію про вибірку даних у компактній і зручній для обробки формі, що містить у собі точні описи об’єктів;

· класифікація: дерева рішень ефективно вирішують задачі класифікації, тобто співвіднесення об’єктів до одного з раніше описаних класів;

· регресія: якщо змінна має непевні значення, то дерева рішень дозволяють визначити залежність цієї цільової змінної від незалежних (вхідних) змінних.

Випадковий ліс  (random forest) – алгоритм машинного навчання, запропонований Лео Брейманом  і Адель Катлер, що полягає у використанні ансамблю  дерев рішень [1]. Алгоритм поєднує в собі дві основні ідеї: метод баггінга (bagging – від bootstrap aggregation, тобто дерева навчаються по випадковим підвибіркам) і метод випадкових підпросторів. Алгоритм застосовується для задач класифікації, регресії і кластеризації.

Випадковим лісом називається класифікатор, який складається з набору дерев , де незалежні однаково розподілені випадкові вектори і кожне дерево вносить один голос при визначенні класу . Відповідно до цього визначення, випадковим лісом є класифікатор, який складається з ансамблю дерев рішень, кожне з якого будується з використанням баггінга. В цьому випадку представляє собою незалежні однаково розподілені l-мірні випадкові вектори, координати яких є незалежними дискретними випадковими величинами, які приймають значення з підмножини з рівними ймовірностями. Реалізація випадкового вектора визначає номера прецедентів навчальної вибірки, які утворюють бутстреп (bootstrap – тобто вибірка з поверненням) вибірку, яка використовується при побудові -го дерева рішень.

Алгоритм індукції випадкового лісу може бети представлений у такому вигляді [2]:

1. Для (де – кількість дерев в ансамблі) виконати:

· Сформувати бутстреп вибірку розміру по вихідній навчальній вибірці ;

· По бутстреп вибірці індукувати не усічене дерево рішень з мінімальною кількістю спостережень в термінальних вершинах, що дорівнює , рекурсивно слідуючи наступному алгоритму:

a) з вихідного набору ознак випадковообрати ознак;

b) з ознак обрати ознаку, яка забезпечує найкраще розщеплення;

c) розщепити вибірку, яка відповідає обробленій вершині, на дві підвибірки;

2. В результаті виконання кроку 1 отримуємо ансамбль дерев рішень ;

3. Передбачення нових спостережень здійснювати наступним чином:

a) для регресії:

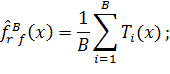
b) для класифікації: нехай – клас, передбачений деревом рішень , тобто ; тоді – клас, який найчастіше зустрічається в множині

Одна з переваг випадкових лісів полягає в тому, що для оцінки ймовірності помилкової класифікації немає необхідності використовувати крос-перевірку (cross-validation) або тестову вибірку. Оцінка ймовірності помилкової класифікації випадкового лісу здійснюється методом "Out-Of-Bag" (OOB), який полягає у наступному. Так як, кожна бутстреп вибірка не містить приблизно 37% спостережень вихідної навчальної вибірки (оскільки вибірка з поверненням, то деякі спостереження в неї не потрапляють, а деякі – декілька раз). Класифікуємо деякий вектор . Для класифікації використовуються тільки ті дерева випадкового лісу, які будувалися по бутстреп вибіркам, що не містять , і як звичайно використовується метод голосування. Частота помилково класифікованих векторів навчальної вибірки при такому способі класифікації і представляє собою оцінку ймовірності помилкової класифікації випадкового лісу методом ООВ. Практика застосування оцінки ООВ показала, що у випадку, якщо кількість дерев велика, то ця оцінка має високу точність.

Випадкові ліси мають цілу низку переваг, в порівнянні з деревами рішень, що і зумовило їх широке застосування, а саме:

1. Випадкові ліса забезпечують істотне підвищення точності, так як дерева в ансамблі слабокорельовані внаслідок подвійної ін'єкції випадковості в індуктивний алгоритм – за допомогою баггінга і використання методу випадкових підпросторів при розщепленні кожної вершини;

2. Методично і алгоритмічно складне завдання обрізання повного дерева рішень знімається , оскільки дерева у випадковому лісі не обрізаються (це також призводить до високої обчислювальної ефективності);

3. Відсутня проблема перенавчання (overfitting) (навіть при кількості ознак, що перевищує кількість спостережень навчальної вибірки і великій кількості дерев). Тим самим знімається складна проблема відбору ознак, необхідна для інших ансамблевих класифікаторів;

4. Простота застосування: єдиними параметрами алгоритму є кількість дерев в ансамблі і кількість ознак, випадково відібраних для розщеплення в кожній вершині дерева;

5. Легкість організації паралельних обчислень.

Недоліками випадкових лісів у порівнянні з деревами рішень є відсутність візуального представлення процесу прийняття рішень і складність інтерпретації їх рішень.

Метод випадкових лісів швидко отримав визнання як в статистичному співтоваристві, так і в середовищі дослідників, і в даний час є одним з найбільш відомих методів класифікації і непараметричної регресії. Також він має вбудовану оцінку якостей та показує високу ефективність при роботі з великою кількістю ознак (наприклад, в хімії, біології і т.д.). Цей метод, став основою для розробки різних його модифікацій, які є важливими для додатків. Крім того, він дав імпульс для розробки методів, в основі яких лежить близька схема, яка не використовує дерева рішень в якості базового класифікатора [2].

Розглянувши сутність та переваги методу випадкових лісів, можна зробити висновок про перспективність його застосування в задачах класифікації даних, зокрема зображень.

Література:

1. Breiman L. Random forests / Breiman L. // Machine Learning. – Vol. 45, N 1. –2001. – P. 5–32.

2. Чистяков С.П. Случайные леса: обзор / С.П. Чистяков // Труды Карельского научного центра РАН. – № 1. – 2013. – С. 117–136.