Математика/1.Дифференциальные и интегральные уравнения

Даулетбаева Ж.Д., старший преподаватель

Костанайский государственный университет, Казахстан

Применение поверхностных потенциалов

к решению краевых задач

Поверхностные потенциалы дают возможность сводить краевые задачи для уравнения Лапласа к интегральным уравнениям. Такой прием эффективен при решении краевых задач со сложной границей и удобен в теоретических исследованиях. Отметим, что решение задачи Дирихле при этом ищут в виде потенциала двойного слоя, решение задачи Неймана – в виде потенциала простого слоя.[1]

В качестве примера рассмотрим первую и вторую краевые задачи: найти функцию , гармоническую в области , ограниченной контуром Г, и удовлетворяющую либо граничным условиям задачи Дирихле (первой краевой задачи) , либо условиям задачи Неймана (второй краевой задачи)

Как для внутренней, так и для внешней задачи нормаль в граничном условии будем считать внутренней.

Решение внутренней первой краевой задачи ищем в виде потенциала двойного слоя

(1)

с неизвестной пока функцией При любом выборе функция удовлетворяет уравнению Лапласа в области , охваченной контуром Г, и разрывна на контуре Г. Для выполнения граничных условий необходимо, чтобы в каждой точке выполнялось равенство . Поэтому по формуле (15) см п 1.3. получим уравнение для определения :

(2)

Если в формуле (2) перейти к естественному параметру, обозначив через и дуги контура Г, соответствующие точкам и , то (2) примет вид

(3)

где L – длина контура Г, - ядро интегрального уравнения. Уравнение (3) является уравнением Фредгольма второго рода. Решив его, найдем функцию , а значит, решим и внутреннюю задачу Дирихле [2].

Для внешней первой краевой задачи аналогично получим уравнение

(4)

Перейдем ко второй краевой задаче. Если искать ее решение в виде потенциала простого слоя

(5)

то для внутренней задачи функция определяется как решение уравнения

(6)

для внешней задачи – как решение уравнения

(7)

Ядро в интегральных уравнениях (6) и (7) имеет вид

.

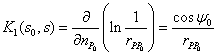Пример (первая краевая задача для круга). Решим внутреннюю задачу Дирихле для уравнения Лапласа в круге радиуса R с границей Г [3]. Предполагая использовать формулы (1) и (2), найдем ядро

потенциала двойного слоя. Ясно, что , поэтому интегральное уравнение (3) для определения функции примет вид

(8)

Ядро этого уравнения вырожденное, т.к. зависит только от одного аргумента Поэтому легко видеть, что решением уравнения (8) является функция

, (9)

где А – некоторая подлежащая определению постоянная. Подставим функцию (9) в уравнение (8) и выразим постоянную А через заданную функцию f :

Таким образом, решением интегрального уравнения (8) является функция

Соответствующий потенциал двойного слоя, дающий решение первой краевой задачи для круга, равен

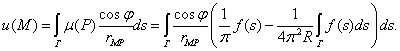
Преобразуем правую часть этой формулы, полагая, что точка М лежит внутри Г:

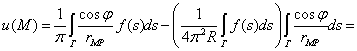(10)

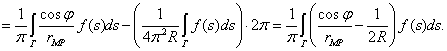
(Здесь было использовано равенство ).

Преобразуем подынтегральное выражение. Из треугольника , имеем и .

Отсюда

Подставив найденное выражение в (10), получим известную формулу Пуассона для круга

которая является решением задачи.

Ценность рассмотренного в этой работе метода потенциалов, созданного независимо Д. Грином (1828) и К. Гауссом (1840), заключается в том, что он свободен от ряда присущих другим методам трудностей. Однако его применение, особенно в случае областей с негладкой границей, связано с громоздкими вычислениями.

Литература:

1 Годунов С.К., Золотарева Е.В. Сборник задач по уравнениям математической физики. Новосибирск: Наука, 1974.-74с.

2 Макаров А. П., Уравнения математической физики. Череповец, 2004.-68с.