Математика/5. Математическое моделирование

к.ф.-м.н. доц. В.И. Евсеев

Казанский (Приволжский) федеральный университет, Казань, Россия,

кафедра прикладной информатики

УДК 681.32 1 - vladislaw.evseev@yandex.ru, т.89047610772

СПЕЦИАЛЬНЫЕ МЕТОДЫ СЕМАНТИЧЕСКОГО АНАЛИЗА

§ 1. Матричные методы анализа

Изотопом бинарной операции назовём один из возможных вариантов, более подробно требования к изотопам будут изучены при рассмотрении стандартной конъюнкции. Так, для группы [Ta1.3] получаем изотоп, соответствующий конъюнкции в данной группе БОКТ, он имеет вид:

Sk( X,Y) [Ta1.3]

Y X	B	D	C	A
B	B	D	C	D
D	D	D	D	D
C	C	D	C	C
A	D	D	C	A

Остановимся более подробно на сути рассматриваемой бинарной операции. Пусть

, (1)

(2)

Тогда получаем, что

, (3)

это – результат данной БОКТ, который отражен в приведенной выше матрице.

Для конъюнкции естественно считать, что

, , (4)

Поэтому форма суждения однозначно определяется значениями кванторов и мостиков, которые получаются как наборы из этой таблицы:

Y X	,	,	,	,
,	,	,	,	,
,	,	,	,	,
,	,	,	,	,
,	,	,	,	,

Здесь (и далее) приняты обозначения:

= , = , = «— », = «–/– ». (5)

Составить реальные примеры не представляет труда, и мы не будем на этом останавливаться., отметим, что построенная матрица соответствует конъюнкции. Пара взаимных поляроидов получается при инверсии соответственно правого или левого сомножителя

Y Х	В	D	С	А
В	С	D	С	С
D	D	D	С	А
С	В	D	С	D
А	D	D	D	D

Y Х	В	D	С	А
В	С	D	В	D
D	D	D	D	D
С	С	С	С	D
А	С	А	D	D

Как нетрудно заметить, в первой матрице происходит перестановка первого и третьего, второго и четвертого столбцов (согласно условиям инверсии по второму аргументу), а во второй матрице – перестановка первой и третьей, а также второй и четвертой строк (согласно условиям инверсии по первому аргументу). Мы позволим себе не останавливаться на строении служебных матриц (из кванторов и мостиков), так как здесь просто происходит подобная же перестановка. Нильюнкция для данной группы является операцией, взаимной дизъюнкции (что уже отмечалось ранее), и мы приводим эту пару бинарных операций одновременно:

Y X	B	D	C	A
B	C	C	C	D
D	C	A	D	D
C	C	D	B	D
A	D	D	D	D

Y X	B	D	C	A
B	B	B	B	A
D	B	D	A	A
C	B	A	C	A
A	A	A	A	A

Дизъюнкция является бинарной операцией второго уровня, у которой соединяющим союзом является знак (или), который позволяет строить соответствующие сложные суждения по типовой схеме:

, , (6)

а служебная матрица (для кванторов и мостиков) принимает вид:

Y X	,	,	,	,
,	,	,	,	,
,	,	,	,	,
,	,	,	,	,
,	,	,	,	,

Такой подход позволяет строить реальные сложные суждения на основе дизъюнкции. Конкретные примеры не представляют интереса. При инверсии дизъюнкции по первому, а затем по второму аргументу, получим оба вида импликаций, запишем для них определяющие матрицы, но служебные матрицы указывать не будем. Строим матрицы импликаций:

Y X	B	D	C	A
B	B	A	В	В
D	A	A	В	D
C	С	А	B	A
A	А	А	A	A

Y X	B	D	C	A
B	B	A	С	А
D	A	A	А	А
C	В	В	B	A
A	В	D	A	A

Бинарные операции третьего уровня – эквиваленция и хартъюнкция – строятся на основе их определений: эквиваленция как конъюнкция двух взаимных импликаций, а хартъюнкция – как её внешняя инверсия.

Таким образом, можно сразу записать обе эти матрицы:

Y X	B	D	C	A
B	B	A	C	D
D	A	A	D	D
C	C	D	B	A
A	D	D	A	A

Y X	B	D	C	A
B	C	D	B	A
D	D	D	A	A
C	D	A	C	D
A	A	A	D	D

Заметим, что обе эти матрицы принадлежат одной группе бинарных операций, у которых (В, D, C, A) = (2, 6,2,6).

Все построенные матрицы оказываются семантически невырожденными, то есть, содержат все типы суждений. Значит, можно сделать вывод о том, выбранный изотоп оказался правильным.

§ 2. Основные требования к БОКТ

Условия, которым должны удовлетворять все изотопы БОКТ подразделим на следующие:

а) сохранение позитивности, при этом пары позитивных суждений при конъюнкции становятся одним позитивным суждением, что соответствует выполнению конъюнкций:

A&A = A (в нетрадиционных случаях возможно С),

A&C = C (в некоторых группах возможно А или D),

C&C = C (в некоторых группах возможно А или D),

б) конъюнкция двух негативных суждений обычно дает негативное суждение:

B&B = B (в некоторых группах возможно C или D),

B&D = D (в некоторых группах возможно B),

D&D =D (всюду),

в) конъюнкция позитивного и негативного суждений обычно бывает негативным суждением:

A&B = B (в некоторых группах возможно D),

B&C = B (в некоторых группах возможно C или D),

C&D = D (в некоторых группах возможно C).

Эти результаты могут быть обобщены в виде таблицы:

ТАБЛИЦА УСЛОВИЙ ДЛЯ БОКТ

№	X	Y	Z
			A	B	C	D
1	A	A	29	0	3	0
2	A	B	0	26	0	6
3	A	C	7	0	25	1
4	A	D	0	0	0	32
5	B	B	0	16	5	11
6	B	C	0	2	24	6
7	B	D	0	7	0	25
8	C	C	9	0	13	10
9	C	D	0	0	7	25
10	D	D	0	0	0	32

Условия этой таблицы полностью реализуются в 32 основных группах БОКТ, за исключением первых двух, о которых уже сказано выше, причем всюду указывается общее количество вхождений данного типа конгруэнции.

§ 3. Построение системы третьей группы [ 1,11,3,1].

Подробно рассмотренный изотоп группы Та1.3. показывает возможности применения матричных методов при семантическом анализе. В следующих параграфах мы кратко рассмотрим все возможные правильные изотопы для блока минимальный бинарных операций. Затем на этом же примере построим общую методику семантического анализа. Также мы изучим полностью возможности соединения подблоков в различных случаях принадлежности структуре клише универсума конкретных суждений (как исходных, так и результирующих).

Так как методика работы с матрицами бинарных операций была уже подробно продемонстрирована, мы позволим себе лишь кратко перечислить результаты.

Сначала построим исходную матрицу и ее инверсию:

Y X	B	D	C	A
B	B	D	C	D
D	D	D	D	D
C	C	D	C	D
A	D	D	D	A

Y X	B	D	C	A
B	C	A	B	A
D	A	A	A	A
C	B	A	B	A
A	A	A	A	D

Теперь укажем матрицы взаимных поляроидов:

Y X	B	D	C	A
B	C	D	C	D
D	D	D	D	A
C	B	D	C	D
A	D	D	D	D

Y X	B	D	C	A
B	C	D	B	D
D	D	D	D	D
C	C	D	C	D
A	D	A	D	D

Матрицы нильюнкции и дизъюнкции имеют вид

Y X	B	D	C	A
B	C	D	C	D
D	D	A	D	D
C	C	D	B	D
A	D	D	D	D

Y X	B	D	C	A
B	B	B	B	A
D	B	D	C	A
C	B	C	C	A
A	A	A	A	A

Аналогично, матрицы взаимных импликаций имеют вид:

Y X	B	D	C	A
B	B	A	B	A
D	A	A	A	D
C	B	A	B	A
A	A	A	A	A

Y X	В	D	C	A
B	B	A	C	A
D	A	A	A	A
C	D	A	B	A
A	A	D	A	A

Можно заметить, что импликации имеют правильный вид, так как элементы «сильных» конгруэнций сохраняют свои значения.

Поэтому и бинарные операции третьего уровня также оказываются правильными, без дефектов, что говорит о наиболее удачном выборе вида исходной матрицы для изучаемой конъюнкции.

Действительно, матрицы операций эквиваленции и хартъюнкции принимают следующий вид:

Y X	B	D	C	A
B	B	A	C	A
D	A	A	A	D
C	C	A	B	A
A	B	D	A	A

Y X	B	D	C	A
B	C	D	B	D
D	D	D	D	A
C	B	D	C	D
A	D	A	D	D

Итак, нами построены все матрицы бинарных структур для данной группы.

§ 4. Параметрический метод анализа семантических операций.

Основой для такого семантического анализа бинарных операций являются количественные параметры вхождения «сильных» суждений типа А и В в структуру изотопа, мы будем обозначать их соответственно и . Число может принимать значения из набора {1, 2, 3, 4}, при этом каждому варианту даются следующие наименования:

а) при = 1 получаем традиционные семантические группы, которые применяются ещё со времен Аристотеля,

б) при = 2 семантические группы называются нетрадиционными, в дальнейшем у нас будет возможность рассмотреть их особенности,

в) при = 3 семантические группы назовём полными, отметим, что эти группы практически в прошлом не применялись,

г) при = 4 существует единственная возможность, то есть, эта группа состоит из одного изотопа, который называется сверхполным и что-либо о его применении автору неизвестно.

Число может принимать значения из набора {1, 2, 3, 4, 5}, здесь применяются следующие термины:

а) при = 1 семантические группы называются минимальными, о применении этих групп у автора отсутствует какая-либо информация,

б) при = 2 семантические группы называются расширенными, они имеет ряд своих особенностей, на которых мы затем кратко остановимся,

в) при = 3 семантические группы называются стандартными, именно к этим группам принадлежит большинство бинарных операций, которые являются наиболее популярными в применении у специалистов по логике,

г) при = 4 семантические группы называются усиленными, об их особенностях также будет сказано в кратком комментарии,

д) при = 5 существует единственная группа, особенности которой будут отмечены в последующем, и которая вряд ли имела применение в прошлом.

Количественные значения вхождения слабых суждений типа C,D создают многообразие вариантов в каждой из перечисленных групп. Полная классификация всех возможных невырожденных бинарных операций имеет следующий вид.

ТАБЛИЦА КЛАСИФИКАЦИИ

СЕМАНТИЧЕСКИХ СТРУКТУР

	1	2	3	4
1	Традиц. миним. 3, 4, 5 ,6 , 7
2	Традиц. расшир. 8,9,10,11,12	Нетрадиц. расшир. 20,21,22,23,24
3	Традиц. стандарт. 13,14,15,16	Нетрадиц. стандарт. 25, 26, 27	Полная стандарт. 30, 31, 32 .
4	Традиц. усилен. 17, 18	Нетрадиц. усилен. 28, 29	Полная усилен. 33	Сверхполн. усилен. 34
5	Традиц. предельн. 19

Указанные здесь номера групп соответствуют группам бинарных операций конъюнктивного типа, указанных в [3, стр.228]. Жирным шрифтом выделены полностью проанализированные автором случаи изотопов. Отметим, что минимальные группы содержат по одному виду сильных конгруэнций. В расширенных группах значение параметра конгруэнции типа В равно двум, а тип А может соответствовать двух значениям (1,2). Группы стандартных операций имеют значение параметра , равное 3, а значения параметров у конгруэнций типа А возможны от 1 до 3. Усиленный случай групп характеризует значение указанного параметра, равное 4, при этом и параметр позитивной сильной конгруэнции может меняться от 1 до 4.

Традиционная предельная группа представлена только одним случаем, когда

Позитивная сильная конгруэнция входит лишь один раз, а остальные параметры равны 5.

§ 5. Спектральные методы анализа БОКТ

Согласно построенной таблице классификации существенную роль играют значения и , которые распределяют все изотопы на выделенные в ней группы. Кроме того, нужно учитывать общее число негативных и позитивных конгруэнций в данном виде БОКТ, а они могут быть вычислены по формулам:

(7)

(8)

Сумма этих значений является квадратом размерности ТАСУ, то есть, 16, а разность характеризует уровень или дефект негативности. Это значение определяется формулой:

(9)

Оно может быть связано с распределением частоты цветового спектра:

(10)

которое задается в виде таблицы:

	7	6	5	4	3	2	1
Цв.	Кр.	Ор.	Жел.	Зел.	Гол.	Син.	Фиол.

В результате сравнения указанных ранее значений получаем таблицу, которую представим состоящей из нескольких частей.

Спектры традиционных минимальных БОКТ

№
1	1	13	1	1	14	2	12	7
2	1	12	2	1	13	3	10	6
3	1	11	3	1	12	4	8	5
4	1	10	4	1	11	5	6	4
5	1	9	5	1	10	6	4	3
6	1	8	6	1	9	7	2	2
7	1	7	7	1	8	8	0	1

Спектры традиционных расширенных БОКТ

№
8	2	11	2	1	13	3	10	6
9	2	10	3	1	12	4	8	5
10	2	9	4	1	11	5	6	4
11	2	8	5	1	10	6	4	3
12	2	7	6	1	9	7	2	2

Спектры традиционных стандартных

и усиленных БОКТ

№
13	3	9	3	1	12	4	8	5
14	3	8	4	1	11	5	6	4
15	3	7	5	1	10	6	4	3
16	3	6	6	1	9	7	2	2
17	4	7	4	1	11	5	6	4
18	4	6	5	1	10	6	4	3
19	5	5	5	1	10	6	4	3

Спектры нетрадиционных расширенных БОКТ

№
20	2	10	2	2	12	4	8	5
21	2	9	3	2	11	5	6	4
22	2	8	4	2	10	6	4	3
23	2	7	5	2	9	7	2	2
24	2	6	6	2	8	8	0	1

Спектры нетрадиционных стандартных

и усиленных БОКТ

№
25	3	8	3	2	11	5	6	4
26	3	7	4	2	10	6	4	3
27	3	6	5	2	9	7	2	2
28	4	6	4	2	10	6	4	3
29	4	5	5	2	9	7	2	2

Спектры полных БОКТ

№
30	3	7	3	3	10	6	4	3
31	3	6	4	3	9	7	2	2
32	3	5	5	3	8	8	0	1
33	4	5	4	3	9	7	2	2
34	4	4	4	4	8	8	0	1

Итоговую таблицу проведенного спектрального анализа мы представим в следующем виде.

Итоговая таблица спектрального анализа БОКТ

		12	10	8	6	4	2	0
		Кр.	Ор.	Жел.	Зел.	Гол.	Син.	Фиол.
1	1	1	2	3	4	5	6	7
1	2		8	9	10	11	12
1	3			13	14	15	16
1	4				17	18
1	5					19
2	2			20	21	22	23	24
2	3				25	26	27
2	4					28	29
3	3					30	31	32
3	4						33
4	4							34
Σ		1	2	4	6	9	8	4

Таким образом, можно сделать вывод, что наибольшую возможность для БОКТ составляют значения = 2, 4, 6. Именно они используются во многих логических построениях. Наиболее информационно насыщенными при этом являются группы, соответствующие голубому и синему цветам, это показывает аналогию с водой, которая также обладает повышенной информационной насыщенностью.

§ 6. Диагональный метод семантического анализа

Для упрощения проведения семантического анализа применим «метод диагоналей» к результирующей матрице этой бинарной операции. Представим «большие» диагонали логического куба которые соответствуют для универсума попарно значениям результирующих суждений по каждому блоку. Отметим, что

блоки ,,имеют следующие пересечения:

, (11)

(12)

а части блоков ,, не входящие в блок обозначим соответственно и . Для этих блоков получаем прямые суммы:

, (13)

(14)

, (15)

а прямая сумма блоков , образует четвертый блок универсума, который не участвует в исследованиях по условиям логического квадрата для традиционного Аристотелева семантического универсума:

. (16)

Теперь находим диагонали, составляющие построенные блоки:

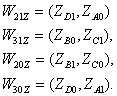(17)

Подблоки общей результирующей матрицы указывают на особенности расположения этих диагоналей, что и позволяет не проводить полный анализ, состоящий из перечисления возможных соединений пар элементов в этом универсуме.

ЛИТЕРАТУРА

1. Евсеев В.И. О методике моделирования логических систем //Информационные технологии в образовании и науке, Казань, 2012. (225 – 231).