А.И. Долгарев

МНОГОМЕРНЫЕ ПОВЕРХНОСТИ II.

СЕКЦИОННАЯ И ПОЛНАЯ КРИВИЗНА ПОВЕРХНОСТИ

 

Ранее, в [1], коэффициенты второй квадратичной формы поверхности многомерного евклидова пространства , , выражены через коэффициенты первой квадратичной формы. Это обобщение результатов из [2]. Используются основные понятия из [3] и [4]. В символике и терминологии иногда имеются понятные отступления от [3, 4]. В [1] определяемость поверхности  пространства  первой квадратичной формой установлена без привлечения формул Гаусса – Петерсона – Кодацци. Разрешен вопрос о количестве нормалей поверхности  в случае . Получены формулы, выражающие нормальную кривизну линий на поверхности, среднюю и полную кривизну поверхности через коэффициенты метрической формы и их производные первого порядка, среди них формула Гауса. Установлено, что все свойства объектов пространства , выраженные через коэффициенты метрической формы и формы кривизны поверхности, выражаются только через коэффициенты метрической формы поверхности и производные первого порядка этих коэффициентов. Рассматриваются свойства секционной кривизны поверхностей , получены вычислительные формулы; они мало отличаются от соответствующих формул для поверхностей 3-мерного евклидова пространства.

 

1. Поверхности размерности . Касательная плоскость

            Векторное пространство  евклидова пространства  состоит из мерных векторов. Ни один объект не может быть задан в пространстве  в векторном виде но с другим количеством координат. Задавая мерные поверхности , нужно исходить из того, что они описываются мерными векторами. В обзоре [3] по теории поверхностей мерного евклидова пространства рассматриваются мерные поверхности как погружения класса , , . Поверхность есть образ :  в паре с погружением  мерного многообразия , . Погружение и поверхность записывается в виде

.

Это поверхность-график, или явно заданная поверхность. Записывается поверхность как векторная функция

,                                         (1)

 есть мерный вектор, описывающий поверхность , ая компонента его равна ; в [4] рассматриваются гиперповерхности, т.е . Производные функции вектора есть

,  .                                               (2)

, в противном случае  от  не зависит. Поверхность  регулярна класса , существуют производные до го порядка включительно и векторы , , линейно независимы. Вектор  имеет только две ненулевые компоненты: ую и ую. Имеется  касательных векторов  поверхности .

            Если  точка поверхности , то ее координаты удовлетворяют уравнению . Точка  такова, что ее координаты удовлетворяют уравнению  при любых . Пусть  вектор, ая координата которого равна 1,  все другие координаты равны 0. Тогда всякая прямая  лежит на поверхности . Поверхность является цилиндрической.

Точка , касательные векторы  в точке  и векторы  порождают касательную плоскость =  поверхности  в точке .

           

2. Нормаль поверхности

            Если  = , = – векторы, ненулевыми компонентами которых являются только компоненты с номерами , где , то имеем бивекторы  = ,

 =

с теми же ненулевыми компонентами. Выполняются следующие свойства.

            1. СВОЙСТВО. Для векторов  выполняется

, .                                  (2)

# Пусть  = ,  = . В этом случае , , , . Имеем вектор , в (2) выписаны только ненулевые компоненты. #

2. СВОЙСТВО. Модули всех векторов больше 1 и

,  , . #                        (3)

            3. СВОЙСТВО. Скалярные произведения векторов , ,  равны:

, ,  ,  .                          (4)

Вектор  перпендикулярен векторам , . Выполняется

. #                               (5)

            4. СВОЙСТВО.  при  и . #

            По виду (2) вектора  запишем вектор

,                                                       (6)

последние  компонент которого равны 0, это поливектор, точнее вектор , его скалярный квадрат равен

,                                                (7)

модуль есть

.

5. СВОЙСТВО. Вектор (6) является ортогональным к векторам касательных  линий поверхности и векторам  прямых , лежащих на поверхности . Вектор

                                                 (8)

является единичным вектором нормали поверхности  в точке .

            #  Действительно,  и . #

6. ТЕОРЕМА. Вектор  =  пространства  ортогонален касательной плоскости  только если он коллинеарен вектору (6).

            # Пусть вектор  ортогонален плоскости . Тогда выполняются равенства:  для всех , т.е. . Понятно, что . Для всех  справедливо:  и вектор  коллинеарен ,  = . Значения координат  определяются из равенств : если , то . #

            7. ТЕОРЕМА. Нормаль поверхности  единственна, =. #

 

3. Фундаментальные формы поверхности

            Метрической формой поверхности   (первой основной квадратичной формой, первой фундаментальной квадратичной формой) называется

 = , ,                                      (9)

коэффициенты метрической формы есть скалярные произведения векторов касательных линий на поверхности  . Значения коэффициентов формы  таковы:

 и  .                              (10)

            Нормальной кривизной линий  на поверхности  относительно нормали  является

.

Имеем =. Обозначим

.                                                               (11)

Теперь кривизна линий на поверхности  относительно нормали  (8) такова

.                                                   (12)

Формой кривизны поверхности   (второй основной квадратичной формой, второй фундаментальной квадратичной формой) относительно нормали называется

,                                                    (13)

ее коэффициенты есть (11).  Формула (12), с учетом (13) и (9), принимает вид

,

нормальная кривизна линий на поверхности равна отношению формы кривизны к  метрической форме  поверхности. Можно говорить о нормальной кривизне линий на поверхности , а не о кривизне линий на поверхности относительно нормали , так как нормаль поверхности единственна, лемма 3.

 

4. Регулярные поверхности  в

            При  и  имеется регулярная поверхность  3-мерного евклидова пространства   = , заданная явной функцией  в окрестности своей обыкновенной точки. Имеем: ,  , . Касательная плоскость в точке  есть , нормаль есть = . Бивектор  является векторным произведением , единичный вектор нормали поверхности  равен . Коэффициенты метрической формы и формы кривизны выписаны выше с точностью до обозначений. Имеем:

;. ,  ,  ,  .

В [2] получены выражения коэффициентов формы кривизны через коэффициенты метрической формы:

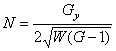,   ,  .                         (14)

Формулы получены без использования формул Гаусса – Петерсона – Кодацци. По (14) в [2] получена и формула Гаусса:

.                                                      (15)

Её своеобразие в том, что полная кривизна поверхности выражена через коэффициенты метрической формы и их производные первого порядка.

 

 

5. Выражение коэффициентов формы кривизны поверхности

через коэффициенты метрической формы

            Для коэффициентов форм  и  евклидовой поверхности размерности  выполняется утверждение, аналогичное утверждению для поверхностей 3-мерного евклидова пространства, см. [2].

            8. ТЕОРЕМА. Коэффициенты формы кривизны  поверхности  выражаются через коэффициенты метрической формы  поверхности и их производные первого порядка. Формулы зависимости таковы:

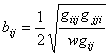,  ,  .                       (16)

            # По первой из формул (10), . Производные величин  равны

.                                                    (17)

По (11) при , , это первая формула в (16). По (17) находим

, .

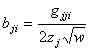Т.к. , то, с использованием второй формулы в (10), находим

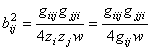,                                                     (18)

откуда получается вторая формула в (16). #

            На основании (7) и первой из (10) имеем

.                                                    (19)

            9. ЛЕММА. Выполняется соотношение 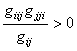 . Выражения  и  имеют один и тот же знак.

            # Это следствие формулы (18). #

Таким образом, подкоренные выражения в формулах (16) положительны. Справедлива следующая

            10. ТЕОРЕМА. Форма кривизны (вторая основная квадратичная форма) мерной поверхности  мерного евклидова пространства  имеет вид

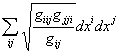=(+).                                (20)

Здесь  коэффициенты метрической формы поверхности.

 

5. Определяемость поверхности мерного пространства

            Установлено, см. [3, теоремы 9.1, 9.6, 9.7, 9.10], что поверхность  евклидова пространства , , определяется однозначно, с точностью до положения в пространстве , своими формами: метрической и кривизны, при выполнении вполне определенных условий на коэффициенты указанных квадратичных форм. Это содержание основной теоремы теории поверхностей. На основании доказанной выше теоремы 8, основная теорема теории поверхностей существенно упрощается.

            11. ТЕОРЕМА. (основная теорема теории поверхностей) Поверхность  евклидова пространства , , однозначно, с точностью до положения в пространстве, определяется своей метрической формой.

            # Утверждение является следствием приведенных в [3] теорем об определяемости поверхности. #

В доказательстве теоремы 8 не налагается никаких условий на коэффициенты форм; в частности, теорема 8 верна и при условиях из теорем, приведенных в [3].

 

6. Секционная кривизна поверхности

            12. СВОЙСТВО. Для всяких трех слагаемых

=                                              (21)

метрической формы  выполняются соотношения

,  ,

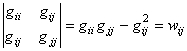т.е. детерминант  выражения (21) положителен. #

            Кривизна поверхности  в направлении бивектора  есть секционная кривизна поверхности . Здесь  рассмотрена секция (21), метрической формы поверхности. Рассмотрим аналогичную секцию формы кривизны

=

и секционную кривизну

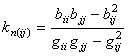 = ,                                                    (22)

где  детерминант секции

            13. ТЕОРЕМА. Секционная кривизна  выражается через коэффициенты секции  метрической формы:

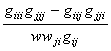= .                                                   (23)

            # Указанную формулу получаем по формулам (16).  #

            Формулы (15) и (23) отличаются одним множителем в знаменателе.

            Секции  и  совпадают с метрической формой  и соответственно с формой кривизны  поверхности  3-мерногого пространства . Выполняется следующая

            14. ТЕОРЕМА. Нормальная кривизна линий секции поверхности  с касательной плоскостью , , описывается равенством (22); формула Гаусса этой секции записывается в виде (23).

            # Ненулевые координаты вектора  секции = совпадают с соответствующими координатами вектора  нормали поверхности . #   

            Секционная кривизна (22) есть полная кривизна поверхности . В соответствии с [3], формула (23) мало отличается от формулы Гаусса в 3-мерном евклидовом пространстве. Имеет место следующая

            15. ТЕОРЕМА. Секционная кривизна поверхности  в направлении бивектора  и нормали  поверхности  совпадают. #

 

7. Средняя и полная кривизна поверхности. Формула Гаусса

            В п. 4 получена формула (20) нормальной кривизны линий на поверхности, выраженной через коэффициенты метрической формы поверхности .

Пусть  матрица метрической формы  (9) поверхности  с коэффициентами (10) и  матрица формы кривизны (13) с коэффициентами (11). В [4, с. 57] выписаны формулы средней  и полной  поверхности  в точке  поверхности:

,   .                              (24)

            16. ТЕОРЕМА. Средняя кривизна поверхности  вычисляется по первой формуле в (24), при условии, что элементы  матрицы  записаны по формулам (16), т.е. средняя кривизна поверхности зависит только от коэффициентов метрической формы поверхности. #

            17. ТЕОРЕМА. Полная кривизна поверхности  вычисляется по второй формуле в (24), при условии, что элементы  матрицы  записаны по формулам (16), т.е. полная кривизна поверхности зависит только от коэффициентов метрической формы поверхности. Вторая формула в (24) является формулой Гаусса поверхностей  при тех же условиях. #

            Таким образом, нормальная кривизна линий на поверхностях , средняя и полная кривизны поверхностей  мерного евклидова пространства , , зависят только от коэффициентов метрической формы поверхности. Выполняется

18. ТЕОРЕМА. Все свойства объектов пространства , выраженные через коэффициенты метрической формы и формы кривизны поверхности, выражаются только через коэффициенты метрической формы поверхности и производные первого порядка этих коэффициентов. #

Традиционно и в [3] определяемость поверхности евклидова пространства ее метрической формой устанавливается с использованием, в том числе, формулы Гаусса. Выше формула Гаусса получена на основе выражения коэффициентов формы кривизны поверхности через коэффициенты метрической формы, т.е на основе определяемости поверхности её метрической формой.

 

Список литературы

  1. Долгарев А.И. Многомерные поверхности I. Выражение коэффициентов второй

      квадратичной формы  евклидовой поверхности через коэффициенты первой квад-

      ратичной формы. / Materialy X Miedzynarodowej naukowi-praktycznej konferencji

     “Moderni vymozenosti vedy – 2014”, dil 34. Matematyka. Fizyka. Praga. Publiching  

      House “Education and Skience”. s.r.o. – 2014. С. 30 – 40

  1. Долгарев А.И. Новый вид основной теоремы Гаусса в евклидовой теории поверх

      ностей.// Materiali IX mezinarodni vedecko-praktika conference «Dni vedy – 2013» -

      Dil  32. Matematika. Vystavba a architektura: Praga. Publiching House “Education and

       Skience”. s.r.o. – 2013. С. 55 – 60.

  1. I. Ivanova-Karatopraklieva, P.E. Markov, I. Kh. Sabitov. Bending of surfaces. III. Fundamentalnaya i prikladnaya matematika, vol 12. (2006), no 1,  pp. 3 – 56.
  2. Иванов А.О., Тужилин А.А. Лекции по классической дифференциальной геометрии. – М.: Новая университетская библиотека, 2009 – 233с.