математика/прикладная математика

 

Д.ф.-м-н.  Красинский А.Я.

 

Московский государственный университет пищевых производств

Московский авиационный институт

К.ф.-м.н. Красинская Э.М.

Московский государственный технический университет им. Н.Э.Баумана

 

Об условиях применения уравнений Лагранжа второго рода в задачах устойчивости и стабилизации равновесий систем с геометрическими связями

 

Во многих задачах современной технической практики (в частности, управления многозвенными манипуляторами и другими мехатронными системами) в силу устройства системы на ее координаты накладываются геометрические связи. Аналитические соотношения, выражающие эти связи, зачастую содержат тригонометрические функции, что, очевидно, чрезвычайно затрудняет выражение одних координат через другие. Сохранение же зависимых координат делает невозможным применение уравнений Лагранжа второго рода, так как при их выводе предполагается введение независимых обобщенных координат, вариации которых будут также независимы. Для рассматриваемых систем можно пользоваться уравнениями Лагранжа первого рода в декартовых координатах или  уравнениями Лагранжа с множителями связей в избыточных криволинейных координатах [1-3].

Другое направления предполагает исключение множителей, которое может быть выполнено различными способами. В настоящей работе в избыточных криволинейных координатах [1,2] рассматриваются голономные механические системы с геометрическими связями. Разрабатывается методика использования уравнений движения в форме М.Ф. Шульгина  [1] в задачах устойчивости и стабилизации  положений равновесия таких систем. Уравнения М.Ф.Шульгина не содержат неизвестных множителей связей, не требуют их определения и поэтому являются удобными для исследования вопросов устойчивости. Процедура их получения основана на исключении из кинетической энергии зависимых скоростей с помощью продифференцированных уравнений связей.  Рассматриваемые  уравнения являются частным случаем уравнений  П. В. Воронца [7,8]  для неголономных систем в случае интегрируемости кинематических связей. Этим они выгодно отличаются от не содержащих множителей связей уравнений в избыточных координатах  в форме А. И. Лурье ([2],стр.,320, уравнения (7.10.9)) (ср. также [4-8], где приведены другие формы уравнений систем с избыточными координатами).

Выбор именно этой формы уравнений позволяет [9,10] легко выделить нулевые корни характеристического уравнения системы первого приближения (из-за наличия кинематических связей) и, тем самым, показать, что устойчивость установившихся движений систем с избыточными координатами возможна лишь в критических случаях  [11-14]. Кроме того, для таких систем оказывается возможным применение ранее полученных результатов, основанных на систематическом использовании векторно-матричных уравнений возмущенного движения с выделенным первым приближением [15-22] и применении теории критических (в том числе и особенных) случаев [11-14].

Стабилизирующее управление и заключение об устойчивости определяются [9,10] рассмотрением управляемой подсистемы, содержащей только возмущения независимых координат и их скоростей. В эту подсистему не входят уравнения продифференцированных связей, но линейную замену по зависимым координатам, приводящую уравнения возмущенного движения к так называемому специальному виду теории критических случаев выполнять необходимо.

То обстоятельство, что устойчивость равновесий систем с геометрическими связями возможна лишь в критических случаях, приводит, вообще говоря, к необходимости анализа нелинейных членов уравнений возмущенного движения, в том числе и в продифференцированных уравнениях связей. Переход к линеаризованным уравнениям связей (и исключению с их помощью зависимых координат)в общем случае некорректен (ср.    ). Однако,  при использовании разработанного [9,10,23] метода решения задач стабилизации сведением к простейшему случаю устойчивости (когда число нулевых корней равно числу геометрических связей), выявились ситуации, в которых первое приближение уравнений возмущенного движения управляемой подсистемы, полученное строгими методами нелинейной теории устойчивости,  в точности совпадает с первым приближением уравнений возмущенного движения системы меньшей размерности, полученной за счет линеаризации не дифференцированных уравнений геометрических связей. Особо следует отметить, что эти последние уравнения выводятся из уравнений Лагранжа второго рода для системы меньшей размерности с исключенными из рассмотрения за счет линеаризации связей зависимыми координатами. Другими словами, некорректное в общем случае применение уравнений Лагранжа второго рода к системам с геометрическими связями в определенных условиях может дать правильное заключение об устойчивости.

Возникает необходимость уточнения этих условий, при которых переход к линеаризованным уравнениям связей и, следовательно, к системе уравнений меньшей на число связей размерности дает возможность  сделать обоснованное заключение об устойчивости. Для получения таких условий проведем формальное рассмотрение задачи.

Уравнения М.Ф. Шульгина. Еще Лагранж отмечал, что, даже если решение задачи можно, используя условные уравнения, привести к рассмотрению уравнений только для обобщенных координат, достаточно часто встречаются такие случаи, когда, во избежание излишнего осложнения расчета, возникает необходимость и оказывается целесообразным сохранение большего числа переменных, чем это необходимо для определения конфигурации системы.В таких ситуациях целесообразно [1-6] задавать конфигурацию механической системы параметрами , взятыми в числе, превосходящем необходимое  n - число степеней свободы системы. Тогда m из этих n+m параметров называются избыточными координатами. Между n+m параметрами существуют m независимых соотношений (которые, вообще говоря, могут содержать и время)

,                                (1)

Если продифференцировать по времени уравнения геометрических связей, наложенных на систему с избыточными координатами, получим кинематические (голономные) связи в виде 

                                                              (2)

Допуская, исходя из (1), без ограничения общности, что в рассматриваемой области пространства                           

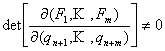                                                                                    (3)

можем представить связи (2) в разрешенном относительно скоростей зависимых координат виде

                                                                      (4)

Исключим, следуя [1], иззависимые скорости с помощью уравнений связей (4). Обозначая полученное выражение кинетической энергии через  , сравнивая соответствующие производные от Ошибка! Источник ссылки не найден. и и учитывая интегрируемость кинематических связей (2), получим уравнения движения системы в избыточных координатах М.Ф. Шульгина

           (5) 

Уравнения (5) не содержат множителей связей, и их число равно числу степеней свободы системы. Уравнения (5) следует рассматривать совместно с уравнениями связей. В этих уравнениях для суммы отнесенных к координатам потенциальных и непотенциальных сил введено  обозначение  

Явный вид уравнений движения  с избыточными координатами М. Ф. Шульгина в скалярной форме.  Первоначальная кинетическая энергия без учета связей (1), которая в общем случае равна

                                                       (6)

   после исключения зависимых скоростей с помощью (4) получит вид

                                                    (7)                        ,                                          

Здесь и далее по дважды повторяющимся индексам предполагается суммирование. Индексы меняются следующим образом: . Уравнения Шульгина (5) представим в явной форме:

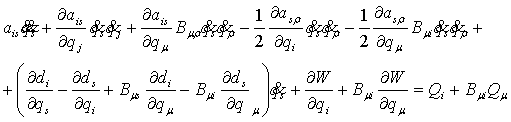                     (8)

Через    - обозначена измененная (приведенная ) потенциальная энергия, -потенциальная энергия,  через теперь обозначены непотенциальные силы, соответствующие координатам  при их избыточном введении.

 Уравнения равновесия можно получить  из этих уравнений, полагая все

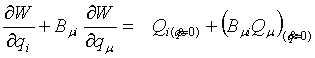                                                              (9)  

    При  и отсутствии непотенциальных сил получим

                                                 

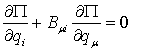
Замечание 1. Отсюда следует, что положение равновесия при использовании избыточных координат может не быть стационарной точкой потенциальной энергии. Однако, если потенциальная энергия может быть выражена через независимые обобщенные координаты , то для нее при отсутствии непотенциальных позиционных сил все       .

Замечание 2. Из уравнений равновесия (9) следует, что потенциальные и непотенциальные позиционные силы  могут  содержать постоянные ненулевые члены

        

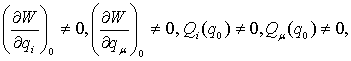
Устойчивость положений равновесия. Структура уравнений возмущенного движения.   Пусть  система допускает положение равновесия.

 

                                          (10)

Введем возмущения, составим уравнения возмущенного движения и выделим в них первое приближение, причем сначала для простоты уравнения составлены без учета непотенциальных сил

                                                ,

        .              (11)

Добавим к этим уравнениям уравнения дифференциальных связей с выделенным первым приближением 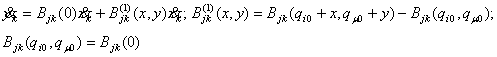          (12)                                        

Если в системе (11), (12) провести линейную замену [7,9,10,23]

                                                        (13)

то уравнения связей примут вид

,                                                    (14)

Очевидно, переменным  соответствуют нулевые корни характеристического уравнения, т.к. справа в уравнениях (14) после замены (13) отсутствуют линейные члены.

Пусть теперь на систему, кроме потенциальных, действуют еще непотенциальные позиционные силы и силы, зависящие от скоростей. Выделяя в уравнениях движения таких систем первое приближение и используя векторно-матричную форму записи,  будем иметь

Исключая из этих сил зависимые скорости, и, выполнив замену (13), для ненулевых корней характеристического уравнения системы первого приближения при действии непотенциальных сил получим

                              (15)

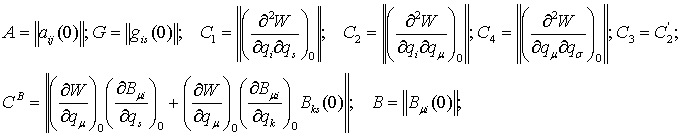
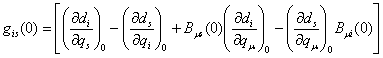
Тогда в полученных после замены (13) уравнениях возмущенного движения в общем случае появляются линейные по возмущениям координат члены с матрицей , зависящие от коэффициентов линейных членов разложения коэффициентов кинематических связей (4)

        

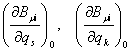
Кроме того, в уравнениях возмущенного движения после замены (13) могут появиться линейные (по возмущениям  координат) члены с коэффициентами

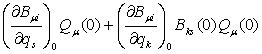          ,                (16)

Следовательно, в общем случае для получения линейного приближения уравнений возмущенного движения нельзя ограничиваться рассмотрением только первого членаразложения уравнения кинематической связи (2) (ср. [24]).

Таким образом, условием допустимости перехода к линеаризованным связям , следовательно, к уравнениям Лагранжа второго рода для системы с исключенными за счет этой линеаризации зависимыми координатами является обращение в нуль в рассматриваемом положении равновесия производных в разложении коэффициентов уравнений продифференцированных связей:

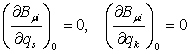                                                                      (17)

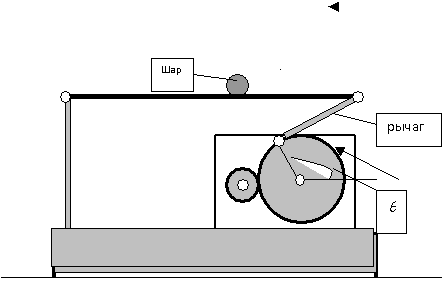
Пример. В [9,10,23,24] рассматривается задача стабилизации равновесия системы BALL&BEAM

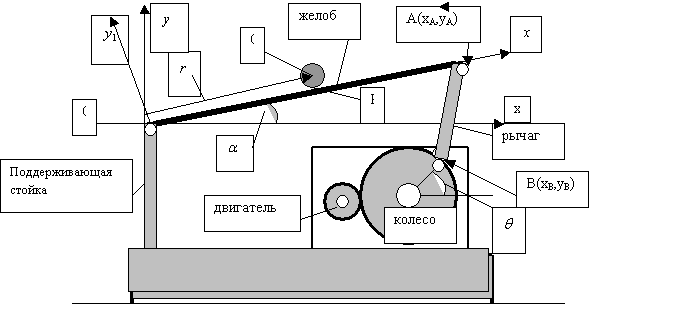
Устройство Ball & Beam  состоит из двух взаимосвязанных частей - механической части и управляемого электропривода. Для описания механической части введем три координаты  . Одна из них  является избыточной, так  как  на систему наложена геометрическая связь - расстояние между точками А и В постоянно: .  Аналитически  эта связь выражается нелинейным тригонометрическим уравнением

                                          (18)

где   ОА =L, AB =l , d – радиус колеса. В системе GBB 1005  при и ,  рычаг АВ вертикален. В большинстве работ (см., напр.[24-26]) по исследованию динамики систем такой конструкции  применяется  одна и  та же необоснованно упрощенная модель - вместо полной нелинейной связи принимается линейная зависимость между углами    (исключение составляет работа [27], в которой связь с точностью до обозначений совпадает с (18)). В то же время применение уравнений Шульгина дает возможность построить строгую нелинейную модель [9,10,23] механической компоненты этого мехатронного стенда

Рассмотрим случай, когда за избыточную координату принят угол поворота колеса,а за координату, определяющую положение шарика r=ОС. Для механической части системы, включающей шар и ротор двигателя с редуктором, кинетическая и потенциальная энергии имеют вид

              ,

где  - cкорость центра масс шара. Выражение для полной угловой скорости шара относительно системы координат Кёнига с центром в точке С и с осями, параллельными неподвижным, можно получить из условия качения шарика без проскальзывания. Тогда для кинетической энергии получим выражение

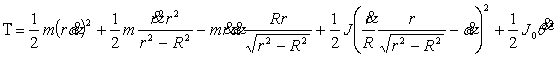
Дифференцируя  связь (18) по времени и выбирая за избыточную координату угол поворота колеса , получим  уравнение кинематической связи в виде

                    (19)

 Исключая из кинетической энергии зависимую скорость, получим выражение для T*,

 

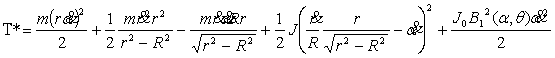
Уравнения Шульгина при таком выборе избыточной координаты будут иметь вид

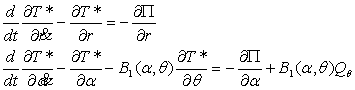                                     (20)

Где  - сила ,действующая по избыточной координате. Она содержит член , который можно считать механическим управляющим воздействием (представляющим собой момент, действующий со стороны якоря двигателя на колесо). Исключим зависимую скорость с помощью уравнения связи (19) . Тогда уравнение Кирхгофа, описывающее динамику электропривода – двигателя постоянного тока с независимым возбуждением, перейдет в уравнение

                                                             (21)

А сила по избыточной координате примет вид

                  

Из уравнений (19),(20),(21) видно, что система допускает положения равновесия  только при ненулевом значении силы тока. Значение силы тока, обеспечивающее существование положения равновесия, определяется из выражения

                                     (22)

Кроме известного положения  равновесия  

                   ;

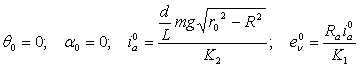
используемый подход позволяет рассматривать все равновесия этого стенда, определяемые уравнениями связи (18) при(что, очевидно, необходимо для равновесия шара)

  или                                    (23)

Это уравнение имеет три корня:

                                          (24)                                       

При этом решениям  для реальных значений параметров стенда соответствует в реальном стенде одна и та же конфигурация, при которой угол поворота колеса лежит во второй четверти.

 

Очевидно, такое положение равновесия никоим образом не может быть получено и, тем более, не может корректно исследоваться при переходе к общепринятому  линейному приближению .

В положении равновесия действующая по зависимой координате непотенциальная сила

                                                                                   (25)

Отсюда видно принципиальное отличие структуры членов первого приближения уравнений возмущенного движения в окрестности равновесия от рассмотренного в [9-10] равновесия вследствие того, что здесь производная

                 

Отметим, что производная

                           

в силу (23) – т.е. эта производная обращается в нуль и в равновесии .

Таким образом, структура уравнений возмущенного движения в окрестности равновесия  существенно отличается от структуры этих уравнений, рассмотренных в [9-10]. В этих работах показано полное совпадение первого приближения для системы уравнений возмущенного движения, соответствующей независимым координатам после проведения замены (13), которая в этой задаче получает вид (для равновесия )

                                  

с первым приближением уравнений возмущенного движения, полученных из уравнений Лагранжа второго рода для системы с исключенными при помощи соотношений

                                

зависимой координатой и ее скоростью. Это обусловлено тем, что для обе производные обращаются в нуль:

т.е. выполнены условия (17).

 

Литература:

1.     Шульгин М.Ф. О некоторых дифференциальных уравнениях аналитической  динамики и их интегрировании. / М.Ф. Шульгин // Научные труды САГУ. – Ташкент. 1958 г. 183 с.

2.     Лурье А.И. Аналитическая механика. / А.И. Лурье. – М.: Гос. изд-во физ.-мат. литературы, 1961. – 824 с

3.     Суслов Г.К. Теоретическая механика. Москва-Ленинград: ОГИЗ. 1946. 656 с.

4.     Ляпунов А.М. Лекции по теоретической механике. Киев: Наукова думка. 1982. 632 с.

5.     Зегжда С.А.,  Солтаханов Ш.Х., Юшков М.П. Уравнения движения неголономных систем и вариационные принципы механики. Новый класс задач управления. М.: Физматлит. 2005. 272 с.

6.     Новожилов И.В., Зацепин М.Ф. Уравнения движения механических систем в избыточном наборе переменных.  Сборник научно-методических статей по теоретической механике. М., 1987. Вып.18. С. 62-66.

7.     Карапетян А.В., Румянцев В.В. Устойчивость консервативных и диссипативных систем // Итоги науки и техники. Общая механика. Т.6. М.: ВИНИТИ, 1983. С. 3-128.

8.     Неймарк Ю.И., Фуфаев Н.А. Динамика неголономных систем. М:Наука, 1967.519 с.

9.     Красинская Э.М., Красинский А.Я. , Обносов К.Б. О развитии  научных методов школы М.Ф.Шульгина в применении к задачам   устойчивости  и стабилизации  равновесий  мехатронных систем с избыточными координатами  .//     Сборник научно-методических  статей. Теор. мех.Вып.28 .Под ред. проф. Ю.Г. Мартыненко. М: Изд-во МГУ, 2012 ,С.169-184.

10.  Красинская Э.М. ,Красинский А.Я. Об устойчивости и стабилизации равновесия механических систем с избыточными координатами. //  Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. Журн. 2013.№ 03,19с. DOI: 10.7463/0313.0541146.

11. Ляпунов А.М. Собрание соч. Т.2.Изд. АН СССР, Москва - Ленинград, –1956.473с.

12. Малкин И.Г. Теория устойчивости движения. Наука Москва, 1952. 532с.

13. Каменков Г.В. Устойчивость и колебания нелинейных систем. М.: Наука, Избр. Труды. Т.2 211 с..

14. Веретенников В.Г. Устойчивость и колебания нелинейных систем. М.: Наука, 1984. 320 с..

15. Красинская Э.М., Красинский А.Я. Применение избыточных координат в задачах устойчивости и стабилизации связанных систем. XV International Conference "Dynamical system modeling and stability investigation", 2011, Kyiv, Ukraine, с. 92.

16. E. Krasinskaya, A. Krasinskiy  On the application of the analytical mechanics and nonlinear  stability theory for stabilization problems of mechatronic systems. CCMECH7, 2011, Moscow-Sedlce. с. 54-55.

17. Красинская –Тюменева Э.М. ,Красинский А.Я. О влиянии структуры сил на устойчивость положений  равновесия неголономных систем . Вопросы выч.  и прикл. математики.вып.45, Ташкент,1977,С. 172-186.

18. Красинская Э.М. К стабилизации стационарных движений механических систем // ПММ.1983.Т.47.вып.2.С.302-309.

19. Красинский А.Я. Об устойчивости и стабилизации положений равновесия неголономных систем //ПММ.1988.Т.52.С.194-202.

20. Красинский А.Я.О стабилизации установившихся движений систем с циклическими координатами. //ПММ.1992.Т.56 .С. 939-950.

21. Красинская Э.М., Красинский А.Я.  Об устойчивости и стабилизации стационарных движений систем с избыточными координатами.Х11 Межд. Конф. Устойчивость и колебания нелинейных систем управления(конференция  Пятницкого),2012,Москва,С.185-187.

22. Красинский  А.Я., Каюмова Д.Р. О влиянии деформируемости колес на динамику робота с дифференциальным приводом.//Нелинейная динамика.2011.Т.7.№4,с.803-822.

23. Красинский А.Я., Красинская Э.М. Моделирование динамики стенда GBB 1005 BALL&BEAM как управляемой  механической системы с избыточной координатой. Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. Журн 2014. №. 01.DOI: 10.7463/0114.0646446

24. Yu W. Nonlinear PD regulation for ball and beam system // Int. Journal of Electrical Engineering Education. 2009.V.46. № 1. P. 59-73.

25. Min-Sung Koo, Ho-Lim Choi, Jong-Tae Lim Adaptive nonlinear control of a ball and beam system using centrifugal force term. //International Journal of Innovative Computing, Information and Control. V. 8, N 9, September 2012. Pp. 5999-6009.

26. Keshmiri M., Jahromi A.F., Mohebbi A., Amoozgar M.H.,  Wen-Fang Xie. Modeling and control of ball and beam system using model based and non-model based control approaches. // International Journal on smart sensing and intelligent systems, Vol. 5, no. 1, March 2012, Pp. 14-35.

27. Andreev F., Auckly D.,Gosavi S., Kapitanski L., Kelkar A., White W. Matching, linear systems, and the ball and beam.// Automatica. 38. 2002. Pp. 2147-2152