УТВЕРЖДАЮ

Физика/4.Применение физических методов в медицине

Богатов Н.М., Синицын А.С., Бондаренко Р.С.,

Бут А.В., Козырев В.Г.

ФГБОУ ВПО «Кубанский государственный университет»,

ГБУЗ «Детская Краевая Клиническая больница» МЗ КК, Россия

ВЛИЯНИЕ ТЕМПЕРАТУРЫ НА МАГНИТНО-РЕЗОНАНСНЫЕ ТОМОГРАФИЧЕСКИЕ ИЗОБРАЖЕНИЯ

Введение

Метод гипертермии (искусственное перегревание организма) – один из древнейших методов лечения. В настоящее время развиваются методы целенаправленного нагревания тканей организма с целью активизации или подавления химико-биологических процессов: местная (локальная), региональная и гипертермия всего тела [1 – 3]. Местная гипертермия требует высокой степени контроля воздействий на ткань, при этом используются ультразвуковые, лазерные, РЧ, СВЧ воздействия. Разработка методов неинвазивной термометрии для термотерапии является актуальной научно-технической проблемой [4].

В работах [5 – 8] обсуждаются диагностические возможности магнитно-резонансной томографии для определения состояния ткани при температурных воздействиях на внутренние органы. Методика определения внутренней температуры тела с помощью ЯМР активно развивается [9]. Для объемной МР термометрии используются методы, основанные на получении резонанса от протонов в составе различных молекул исследуемого объекта: воды и жира [10, 11, 12], метилена [13], липидов [14] и др. Разница резонансных частот дает информацию об абсолютной температуре тканей. Разрабатываются методы, использующие молекулярную диффузию [15].

Разнообразие методов построения тепловых изображений с помощью МРТ обусловлено многофакторностью влияния температуры на состояние живого объекта, что выражается в температурной зависимости измеряемых параметров: времени продольной (спин-решеточной) релаксации T₁ [16 – 22], времени поперечной (спин-спиновой) релаксации T₂ [13, 21, 22], намагниченности M₀ [22], связанной с протонной плотностью, коэффициента диффузии D [19, 23], химического сдвига d [14, 24 – 27]. Сравнительный анализ различных методов проведен в работе [28].

Регистрация теплового поля методом МРТ в объеме для различных способов нагревания заданной области обсуждается в следующих работах: микроволновой нагрев [21, 27], лазерный нагрев [22, 29], нагрев от миниатюрных электронагревателей [30].

Времена релаксации T₁, T₂ зависят от индукции магнитного поля [31], эта зависимость для T₁ более выражена, чем для T₂. В результате контрастные характеристики биологической ткани T₁ МРТ изображений зависят от значения индукции магнитного поля. Поэтому для разработки методики магнитно-резонансной термометрии необходимо исследовать эти эффекты.

Целью данной работы является цифровой анализ T₁ и T₂ МРТ изображений фантомов с различной постоянной по объему температурой.

Анализ МРТ изображений фантомов с различной температурой

Фантомы, однородные и неоднородные по составу, исследовались на магнитно-резонансном томографе 1 Тл Panorama HFO 1.0. Анализировалось изменение времени спин-решеточной релаксации протонов T₁ и спин-спиновой релаксации протонов T₂. Значения интенсивности сигнала T, на основе которых построены изображения, нормированы так, что T Î [0, 255]. Повышение разрешающей способности достигалось использованием псевдоцветовой палитры МРТ изображений. Температура исследуемых объектов t измерялась с помощью контактного термодатчика Nihon Konden BSN 2301K, термограммы регистрировались дистанционно с помощью тепловизора Testo 885-2.

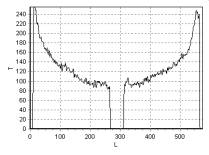
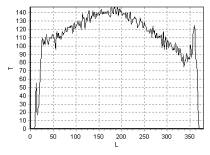
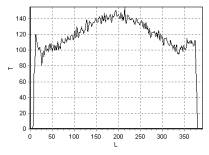
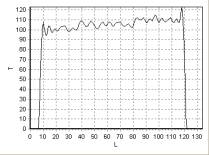
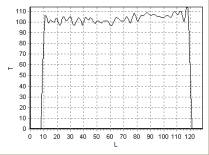
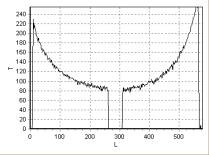
Однородные фантомы – полиэтиленовые пакеты 500 мл с 0,9% раствором натрия хлорида для инфузий. На рис. 1, рис. 5 показаны T₁ изображения двух фантомов с одинаковой температурой t = 24,9 °С, полученные во взаимно перпендикулярных проекциях с помощью импульсной последовательности FFE (Fast Field Echo). На рис. 2, рис. 3, рис. 4 приведена зависимость интенсивности сигнала T от длины L, измеряемой в пикселях, для линий 1, 2, 3 (рис. 1), соответственно, а на рис. 6, рис. 7, рис. 8 – для линий 1, 2, 3 (рис. 5). Для каждой линии началом отсчета является ее левая, верхняя точка.

Изменение интенсивности сигнала T в объеме однородных фантомов, продемонстрированное рис. 1 – рис. 8, связано с зависимостью времени спин-решеточной релаксации T₁ от распределения индукции магнитного поля.

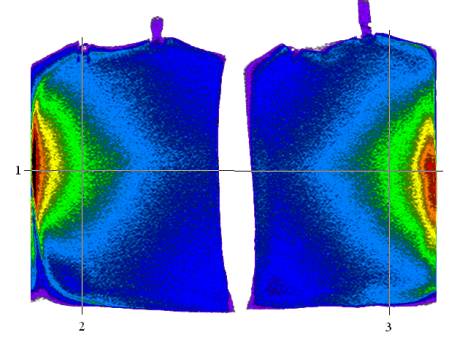
Рис. 1. T₁ –взвешенное изображение, полученное с помощью импульсной последовательности FFE, двух однородных фантомов с одинаковой температурой 24,9 °С в горизонтальном сечении

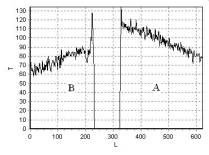
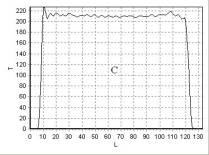
На рис. 9 показаны T₁ изображения трех фантомов A, B, C с различной температурой, полученные с помощью импульсной последовательности FFE (Fast Field Echo). На рис. 10, рис. 11, рис. 12, рис. 13 приведена зависимость интенсивности сигнала T от длины L, измеряемой в пикселях, для линий 1, 2, 3, 4 (рис. 9), соответственно.


Рис. 2. Распределение интенсивности сигнала T вдоль линии 1 рис. 1	Рис. 3. Распределение интенсивности сигнала T вдоль линии 2 рис. 1	Рис. 4. Распределение интенсивности сигнала T вдоль линии 3 рис. 1

Рис. 5. T₁ –взвешенное изображение, полученное с помощью импульсной последовательности FFE, двух однородных фантомов с одинаковой температурой 24,9 °С в вертикальном сечении


Рис. 6. Распределение интенсивности сигнала T вдоль линии 1 рис. 5	Рис. 7. Распределение интенсивности сигнала T вдоль линии 2 рис. 5	Рис. 8. Распределение интенсивности сигнала T вдоль линии 3 рис. 5

Из данных, представленных на рис. 9 – рис. 13, следует, что при заданных значениях температуры фантомов A, B, C неоднородность распределения индукции магнитного поля оказывает более существенное влияние на изменение времени спин-решеточной релаксации T₁, чем температура. Такой же вывод следует из анализа T₁ изображений фантомов A, B, C, полученных в проекциях, перпендикулярных, проекции рис. 9.

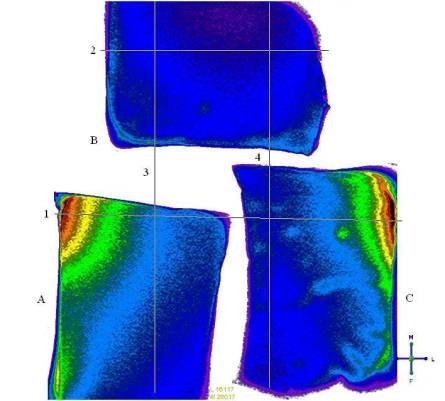
Рис. 9. T₁ –взвешенное изображение, полученное с помощью импульсной последовательности FFE, трех однородных фантомов A, B, C с различной температурой в горизонтальном сечении:

A – t_A = 19,8 °С; B – t_B = 24,9 °С; C – t_C = 26,6 °С


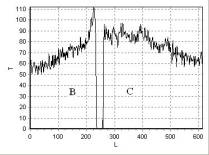
Рис. 10. Распределение интенсивности сигнала T вдоль линии 1 рис. 9	Рис. 11. Распределение интенсивности сигнала T вдоль линии 2 рис. 9

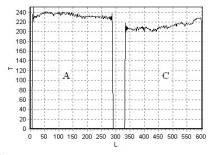
На рис. 14 показаны T₂ изображения сечения фантомов A, C, а на рис. 18 фантома B, полученные с помощью импульсной последовательности TSE (Turbo Spin Echo).


Рис. 12. Распределение интенсивности сигнала T вдоль линии 3 рис. 9	Рис. 13. Распределение интенсивности сигнала T вдоль линии 4 рис. 9

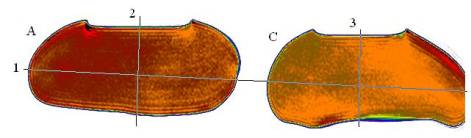
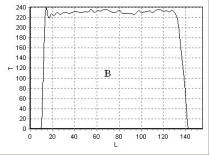
Рис. 14. T₂ –взвешенное изображение, полученное с помощью импульсной последовательности TSE, сечения однородных фантомов A, C с температурой: A – t_A = 19,8 °С; C – t_C = 26,6 °С

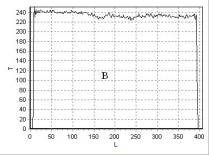
На рис. 15, рис. 16, рис. 17 приведена зависимость интенсивности сигнала T от длины L, измеряемой в пикселях, для линий 1, 2, 3 (рис. 14), а на рис. 19, рис. 20 – для линий 1, 2 (рис. 18), соответственно.

Для T₂ –взвешенных изображений фантомов на рис. 14, рис. 18 характерно достаточно однородное распределение интенсивности цвета. Этот факт подтверждается распределением интенсивности сигнала T вдоль линий (рис. 15 – рис. 17, рис. 19, рис. 20).


Рис. 15. Распределение интенсивности сигнала T вдоль линии 1 рис. 14	Рис. 16. Распределение интенсивности сигнала T вдоль линии 2 рис. 14	Рис. 17. Распределение интенсивности сигнала T вдоль линии 3 рис. 14

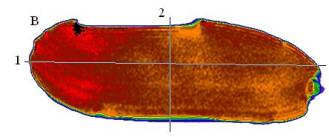
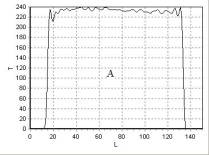
Рис. 18. T₂ –взвешенное изображение, полученное с помощью импульсной последовательности TSE, сечения однородного фантома B: t_B = 24,9 °С


Рис. 19. Распределение интенсивности сигнала T вдоль линии 1 рис. 18	Рис. 20. Распределение интенсивности сигнала T вдоль линии 2 рис. 18

Среднее значение интенсивности сигнала для фантомов A, C (рис. 14), B (рис. 18), рассчитанные во внутренних прямоугольных областях: T_A = 234; T_C = 211; T_B = 233,9. Стандартные отклонения, соответствующие этим величинам: S_A = 3,9; S_C = 5; S_B = 5,5. Таким образом, погрешность, определяемая по стандартному отклонению, не позволяет достоверно идентифицировать температурное состояние фантомов A (t_A = 19,8 °С) и B (t_B = 24,9 °С), однако вполне позволяет идентифицировать состояние фантома C (t_C = 26,6 °С).

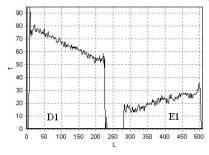
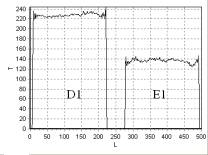
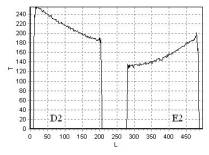
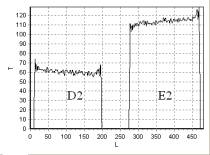
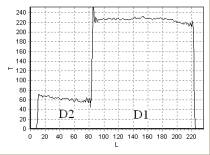
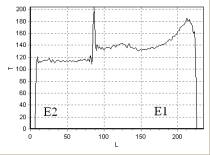
Неоднородные фантомы D, E – пластиковые бутылки 1,5 л, заполненные водой (D1, E1) и рафинированным подсолнечным маслом (D2, E2). Фантом D имел температуру t_D = 13 °С, фантом E – t_E = 38 °С. На рис. 21 показаны T₁ изображения сечения фантомов D, E, полученные с помощью импульсной последовательности FFE. На рис. 22 – рис. 25 приведена зависимость интенсивности сигнала T от длины L, измеряемой в пикселях, для линий 1, 2, 3, 4 (рис. 21), соответственно.

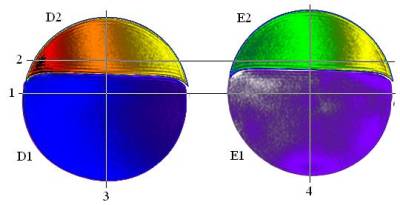
Рис. 21. T₁ –взвешенное изображение, полученное с помощью импульсной последовательности FFE, сечения неоднородных фантомов D, E:

D1 – вода; D2 – подсолнечное масло; E1 – вода; E2 – подсолнечное масло

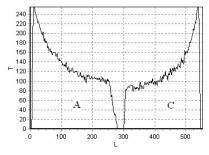
Анализ данных, представленных на рис. 21 – рис. 23, показывает, что неоднородность распределения индукции магнитного поля оказывает существенное влияние на изменение времени спин-решеточной релаксации T₁, как в воде (рис. 22), так и в подсолнечном масле (рис. 23), однако влияние изменения температуры в рассматриваемом случае явно выражено.


Рис. 22. Распределение интенсивности сигнала T вдоль линии 1 рис. 21	Рис. 23. Распределение интенсивности сигнала T вдоль линии 2 рис. 21


Рис. 24. Распределение интенсивности сигнала T вдоль линии 3 рис. 21	Рис. 25. Распределение интенсивности сигнала T вдоль линии 4 рис. 21

Разность значений DT₁ на границе масло-вода для фантома D (рис. 24)

DT₁|_D = T₁|_D₂ – T₁|_D₁ > 0,

это значение больше, чем для фантома E (рис. 25)

DT₁|_E = T₁|_E₂ – T₁|_E₁ > 0.

Известная экспериментальная зависимость DT₁(t) позволяет разработать методику определения внутренней температуры посредством измерения DT₁ на границе раздела сред.

Среднее значение интенсивности сигнала T₁ для веществ D1, E1 и D2, E2, составляющих фантомы D, E, рассчитанные во внутренних прямоугольных областях: T_D₁ = 65; T_E₁ = 22,7; T_D₂ = 213,5; T_E₂ = 150. Стандартные отклонения, соответствующие этим величинам: S_D₁ = 6,9; S_E₁ = 4,5; S_D₂ = 15,1; S_E₂ = 12,4. Температурные интервалы T_D₁ ± S_D₁; T_E₁ ± S_E₁; T_D₂ ± S_D₂; T_E₂ ± S_E₂ не перекрываются. Следовательно, температурное состояние веществ D1, E1, D2, E2 определяется однозначно по T₁ изображению (рис. 21).

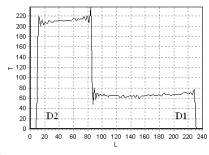
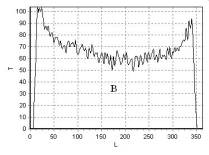
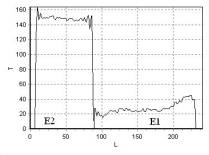
На рис. 26 показаны T₂ изображения сечения фантомов D, E, полученные с помощью импульсной последовательности TSE. На рис. 27 – рис. 30 приведена зависимость интенсивности сигнала T от длины L, измеряемой в пикселях, для линий 1, 2, 3, 4 (рис. 26), соответственно.

T₂ –взвешенное изображение фантомов D, E в областях D1, D2, E1, E2 достаточно однородно (рис. 26), что подтверждается распределением интенсивности сигнала T вдоль линий (рис. 27 – рис. 30).

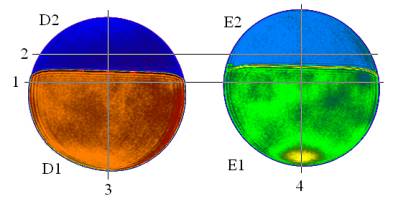
Рис. 26. T₂ –взвешенное изображение, полученное с помощью импульсной последовательности TSE, сечения неоднородных фантомов D, E:

D1 – вода; D2 – подсолнечное масло; E1 – вода; E2 – подсолнечное масло


Рис. 27. Распределение интенсивности сигнала T вдоль линии 1 рис. 26	Рис. 28. Распределение интенсивности сигнала T вдоль линии 2 рис. 26


Рис. 29. Распределение интенсивности сигнала T вдоль линии 3 рис. 26	Рис. 30. Распределение интенсивности сигнала T вдоль линии 4 рис. 26

Время спин-решеточной релаксации T₁ уменьшается с ростом температуры, как в воде (рис. 22), так и в подсолнечном масле (рис. 23). Время спин-спиновой релаксации T₂ демонстрирует иную закономерность: значение T₂ уменьшается с ростом температуры для воды (рис. 27), но увеличивается для подсолнечного масла (рис. 28).

Разность значений DT₂ на границе масло-вода так же демонстрирует иную закономерность по сравнению с DT₁: для фантома D (рис. 29)

DT₂|_D = T₂|_D₂ – T₂|_D₁ < 0,

это значение по модулю больше, чем для фантома E (рис. 30)

DT₂|_E = T₂|_E₂ – T₂|_E₁ < 0.

Для фантома E на границе масло-вода со стороны воды наблюдается резкий пик сигнала T₂ (рис. 30) – химический сдвиг. Значение химического сдвига d для фантома E значительно больше, чем для фантома D (рис. 29), что свидетельствует о необходимости изучения зависимости d (t) с целью использования ее для определения температуры.

Увеличение сигнала T₂ в области E₁ (рис. 30) в направлении внешней границы требует дальнейшего исследования. Возможно, оно связано с диффузией более легких атомов из области E₂ в область E₁ в фантоме с более высокой температурой.

Среднее значение интенсивности сигнала T₂ для веществ D1, E1 и D2, E2, составляющих фантомы D, E, рассчитанные во внутренних прямоугольных областях: T_D₁ = 229,2; T_E₁ = 137,5; T_D₂ = 60,8; T_E₂ = 113,5. Стандартные отклонения, соответствующие этим величинам: S_D₁ = 3,3; S_E₁ = 4,5; S_D₂ = 2,5; S_E₂ = 2,1. Температурные интервалы T_D₁ ± S_D₁; T_E₁ ± S_E₁; T_D₂ ± S_D₂; T_E₂ ± S_E₂ не перекрываются. Следовательно, температурное состояние веществ D1, E1, D2, E2 определяется однозначно по T₂ изображению (рис. 26).

Таким образом, изучение зависимости времени спин-спиновой релаксации T₂ от температуры и состава вещества открывает дополнительные возможности для определения внутренней температуры тела.

Заключение

Многие методы воздействия на организм человека приводят к изменению температуры, как внутренних органов, так и поверхности тела. Тепловизионный метод, регистрирующий ИК излучение с поверхности тела, позволяет достаточно точно определить изменение поверхностной температуры. Измерение температуры внутренних органов и ее изменения в результате воздействия электрических, электромагнитных, акустических, механических, тепловых и др. воздействий является актуальной научно-технической проблемой. В настоящее время разрабатываются методы определения температуры внутренних органов с помощью различных модификаций магнитно-резонансной томографии, используя влияние температуры на значения времён спин-решеточной релаксации T₁, спин-спиновой релаксации T₂, величин намагниченности M₀, коэффициента диффузии D, химического сдвига d и др.

В данной работе проанализировано влияние температуры фантомов на МРТ изображения, полученные с помощью стандартных методик.

Показано, что неоднородность распределения индукции магнитного поля оказывает существенное влияние на изменение времени спин-решеточной релаксации T₁. Этот факт необходимо учитывать при разработке методики объемной термометрии, использующей измерение T₁.

T₂ –взвешенные изображения однородных фантомов имеют достаточно однородное распределение интенсивности цвета, поэтому их целесообразно использовать для идентификации температурного состояния объектов. Однако в этом случае возрастают требования к точности модели, описывающей зависимость времени спин-спиновой релаксации T₂ от индукции магнитного поля, температуры и химического состава исследуемого вещества.

Для объектов неоднородного состава на T₂ изображениях ярко проявляется температурная зависимость химического сдвига на границе раздела сред. Кроме того, при построении модели следует учитывать влияние температуры на диффузию молекул в область с их меньшей концентрацией.

Литература

1. Гипертермия как метод лечения. Медицинская энциклопедия. // http://www.medical-enc.ru/m/15/gipertermia.shtml

2. Гипертермия. Альтернативное лечение рака. // http://onkologia.maxbb.ru/topic85.html

3. Гипертермия. Онкологический центр им. Блохина. // http://www.onkodoktor.ru/gipertermiya

4. Gerard C. van Rhoon, Peter Wust Introduction: Non-invasive thermometry for thermotherapy.//International Journal of Hyperthermia,2005,V.21, N.6, P.489–495.

5. Бокерия Л.А., Бокерия О.Л., Сергеев А.В., Темирбулатова А.Ш. Диагностические возможности магнитно-резонансной томографии при проведении электрофизиологических процедур.//Анналы аритмологии,2011,№1,С.22 – 30.

6. Gellermann J., Wlodarczyk W., Feussner A., Fähling H., Nadobny J., Hildebrandt B., Felix R., Wust P. Methods and potentials of magnetic resonance imaging for monitoring radiofrequency hyperthermia in a hybrid system. // International Journal of Hyperthermia, 2005, V. 21, N. 6, P. 497–513.

7. Arthur R.M., Straube W.L., Trobaugh J.W., Moros E. G. Non-invasive estimation of hyperthermia temperatures with ultrasound. // International Journal of Hyperthermia, 2005, V. 21, N. 6, P. 589–600.

8. Straube T., Kahn T. Thermal therapies interventional MR imaging. Laser. // Neuroimaging Clin. N. Amer., 2001, V. 11, N. 4, P. 549–571.

9. Denis de Senneville B., Quesson B., Moonen C.T.W. Magnetic resonance temperature imaging. // International Journal of Hyperthermia, 2005, V. 21, N. 6, P. 515–531.

10. McDannold N. Quantitative MRI-based temperature mapping based on the proton resonant frequency shift: Review of validation studies. // International Journal of Hyperthermia, 2005, V. 21, N. 6. P. 533–546.

12. Soher B.J., Wyatt C., Reeder S.B., Mackfall J.R. Noninvasive temperature mapping with MRI using chemical shift water-fat separation. // Magnetic Resonance in Medicine, 2010, V. 63, I. 5, P. 1238–1246.

13. McDannold N., Barnes A.S. et al. Temperature Mapping Considerations in the Breast with Line Scan Echo Planar Spectroscopic Imaging. // Magnetic Resonance in Medicine, 2007, V. 58, N. 6, P. 1117–1123.

14. Kuroda K., Mulkern R.V. et al. Temperature Mapping Using the Water Proton Chemical Shift: Self-Referenced Method With Echo-Planar Spectroscopic Imaging. // Magnetic Resonance in Medicine, 2000, V. 43, N. 2, P. 220–225.

15. Delannoy J, Chen CN et al. Noninvasive temperature imaging using diffusion MRI. // Magnetic Resonance in Medicine, 1991, V. 19, I. 2, P. 333–339.

16. Dickinson R.J., Holl A.S. et al. Measurement of changes in tissue temperature using MR imaging. // J. Compt. Assist. Tomogr., 1986, N 10, P. 468–472.

17. Kuroda K., Tsutsumi S., Saltoh A. Non-invasive temperature distribution measurement by simultaneous use of multiple NMR parameters. // Trans. IEICE, 1990, J73-A(8), P. 1431–1443.

18. Ling C., Poster M. et al. Comparison of NMR water proton T₁ relaxation times of rabbit tissues at 24 MHz and 2,5 MHz.//Phys.Med.Biol. 1980, N.25, P.748–751.

19. Simpson J.H., Carr H.Y. Diffusion and nuclear spin relaxation in water. // Phys. Rev., 1958, V. 111, I. 5, P. 1201–1202.

20. Hall A.S., Prior M.V., Hand J.W., Observation by MR imaging of in vivo temperature changes induced by radio frequency hyperthermia. // J Comput Assist Tomogr, 1990, V. 14, N. 3, 430–436.

21. Paliwal V., AbdEl-Monem El-Sharkawy, Du X., Yang X., Atalar E. SSFP-Based MR Thermometry. // Magnetic Resonance in Medicine, 2004, V.52, N.4, P.704–708.

22. Panych L.P., Hrovat M.I., Bleier A.R., Jolesz F.A. Effects Related to Temperature Changes during MR Imiging.//J.Magn.Reson.Imaging,1992,V.2,N.1, P.69–74.

23. Le Bihan D., Delannay J., Levin R.L. Temperature mapping with MR imaging of molecular diffusion imaging: Application to hyperthermia. // Radiology, 1989, V. 171, N. 3, P. 853–857.

24. Kagayaki Kuroda Non-invasive MR thermography using the water proton chemical shift.//International Journal of Hyperthermia,2005, V.21, N.6, P.547–560.

25. Hall L.D., Talagala S.L. Mapping of pH and temperature distribution using chemical-shift-resolved tomography. // J.Magn.Reson., 1985, V. 65, I.2, P.501–505.

26. Yasutoshi Ishihara, Arturo Calderon et al. A Precise and Fast Temperature Mapping Using Water Proton Chemical Shift. // Magn. Reson. Med., 1995, V.34, N.6, P.814–823.
27. Vitkin I.A., Moriarty J.A. et al. Magnetic resonance imaging of temperature changes during interstitial microwave heating: a phantom study. // Med. Phys., 1997, V. 24, I. 2, P. 269–277.

28. Lüdemann L., Wlodarczyk W. et al. Non-invasive magnetic resonance thermography during regional hyperthermia. // Int. J. Hyperthermia, 2010, V. 26, I. 3, P.273–282.

29. Волков А.А., Никифоров В.Н., Пирогов Ю.А., Иванов А.В., Прохоров А.С. Регистрация температурного поля методом магнитно-резонансной томографии. // Медицинская физика, 2011, № 1, С. 75 – 81.

30. Волков А.А., Какагельдыев С.К., Прохоров А.С., Пирогов Ю.А. Традиционные методы нагрева в применении к магнитно-резонансной термометрии.// Журнал радиоэлектроники, 2012, № 1, http://jre.cplire.ru/iso/jan12/12/text.html

31. Казначеева А.О., Ананьева Н.И. Высокопольная магнитно-резонансная томография: возможности, безопасность, ограничения. // http://do.gendocs.ru/docs/index-120090.html