Д. т. н., профессор Нагорный В.П., к. т. н. Денисюк И.И.

Институт геофизики им. С.И. Субботина НАН Украины

АМПЛИТУДНО-МОДУЛИРОВАННЫЕ ВОЛНЫ В НЕЛИНЕЙНОЙ ГЕОФИЗИЧЕСКОЙ СРЕДЕ С ДИСПЕРСИЕЙ

В последние годы наметился повышенный интерес к исследованию модулированных акустических волн в связи с их практическим применением к различным техническим задачам, в частности, к задачам интенсификации добычи углеводородов акустическими методами. Источниками модулированных волн могут быть как генераторные устройства нового поколения [1], так и сами неоднородные геофизические среды при их акустической обработке. В работах [2, 3] показано, что при распространении акустической гармонической волны в нелинейной среде без дисперсии она с расстоянием трансформируется в нелинейную пилообразную волну, являющуюся в широком смысле модулированной волной [4] с широким спектром частот.

Научный и практический интерес представляет исследование распространения акустических гармонических волн в нелинейной дисперсионной среде.

На примере простейшей задачи теории нелинейных волн – генерации второй гармоники с частотой 2ω – покажем, к каким физическим явлениям приводит учет дисперсионных свойств среды.

Неоднородное дифференциальное уравнение, описывающее поведение волны гармоники 2ω, сгенерированной в нелинейной среде без дисперсии при действии на входе среды гармонического сигнала имеет вид [3]

,

(1)

где – смещение гармонической волны с частотой 2ω; 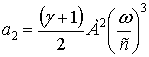; А – амплитуда исходного гармонического сигнала частоты ω; γ – показатель адиабаты Пуассона в уравнении состояния среды; с – скорость звука в среде.

При наличии дисперсии в нелинейной среде уравнение (1) имеет вид [5]

,

(2)

где – фазовые скорости волн с круговой частотой ω и 2ω, соответственно.

Общим решением неоднородного дифференциального уравнения (2) является сумма решений однородного уравнения при и частного решения неоднородного уравнения при .

.

(3)

Составляющие правой части выражения (3) могут быть названы собственной и вынужденной волнами.

Применяя операционный метод, решение представим в виде

,

(4)

где 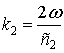– волновое число гармоники с частотой 2ω; – амплитуда волны гармоники с частотой 2ω в точке ; – сдвиг по фазе.

Частное решение определим с применением операционного метода и метода вариации постоянных [6].

Представим уравнение (2) в изображениях по Лапласу в виде

,

(5)

где s – параметр преобразования; – изображение Лапласа функции .

Согласно [3, 6] частное решение неоднородного уравнения (5) имеет вид

.

(6)

Коэффициенты определяем из системы уравнений [6]

(7)

где .

Решая систему уравнений (7), находим

(8)

где .

Из соотношений (8) после интегрирования по переменной х следует

(9)

После подстановки (9) в соотношение (6), определяем

.

(10)

Переходя от изображений по Лапласу в класс оригиналов, из соотношения (10) получим частное решение неоднородного уравнения (2)

,

(11)

где 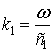– волновое число гармоники с частотой ω; – сдвиг по фазе волны .

Поскольку акустическое детектирование не рассматривается, в (11) оставляется лишь компонента с частотой [5]

.

(12)

Таким образом, с учетом (4) и (12) решение имеет вид:

.

(13)

Чтобы удовлетворить граничному условию (отсутствию второй гармоники в начале координат при ), положим произвольные константы равными

.

(14)

В итоге, с учетом (14) решение (13) представим в виде

.

(15)

После несложных тригонометрических преобразований из (15) получим

.

(16)

Из соотношения (16) видно, что амплитуда волны частоты не остается постоянной, а испытывает биения в пространстве. Амплитуда и пространственный период этих биений определяются величиной . Амплитуда изменяется согласно выражению

.

(17)

Член 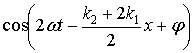описывает биения по оси координат х. Частота биений определяется величиной .

Таким образом, формула (16) определяет амплитудно-модулированные колебания, распространяющиеся по оси х с течением времени. Происходит модуляция биений по амплитуде. С уменьшением Δ амплитуда и период биений возрастают. Монотонное возрастание амплитуды гармоники с частотой 2ω происходит только на отрезке . Величина определяется формулой

.

(18)

Согласно [5] величина – это так называемая длина когерентного взаимодействия между волнами на частотах ω и 2ω.

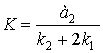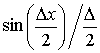На рисунке приведена зависимость амплитуды модулируемой волны , отнесенной к параметру , от параметра Δ. Как видно с уменьшением Δ период и амплитуда биений возрастают. Предельный случай соответствует синхронному, накапливающемуся взаимодействию. При этом раскрытие неопределенности вида в формуле (17) приводит к линейному закону нарастания амплитуды гармоники с частотой 2ω.

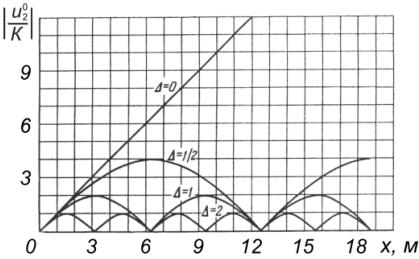
Зависимость амплитуды модулируемой волны от Δ

Таким образом, при распространении акустической волны частоты ω в нелинейной среде с дисперсией генерируются амплитудно-модулированные колебания в виде биений.

Литература

1. Александров В., Бушер М., Казаков Ю., Майоров В. Развитие опыта акустической обработки продуктивной зоны скважин // Технологии ТЭК. – 2003. – № 2. – С. 1–9.

2. Грінченко В.Т., Вовк І.В., Мацапура В.Т. Основи акустики. – К.: Наук. думка. – 2007. – 640 с.

3. Нагорний В.П., Денисюк І.І. Імпульсні методи інтенсифікації видобутку вуглеводнів. – К.: Ін-т геофізики ім. С.І. Субботіна НАН України, 2012. – 323 с.

4. Островский Л.А., Потапов А.И. Введение в теорию модулированных волн. – М.: Физматгиз. – 2003. – 400 с.

5. Руденко О.В., Солуян С.И. Теоретические основы нелинейной акустики. – М.: Наука, 1975. – 288 с.

6. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. – М.: Наука, 1985. – 464 с.
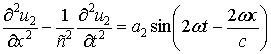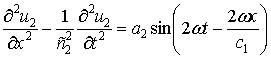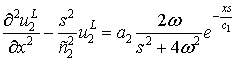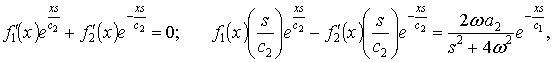
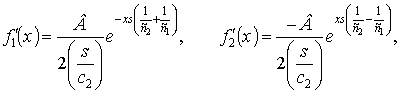
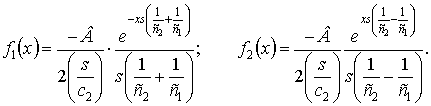
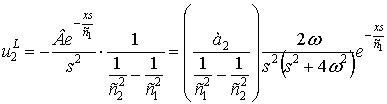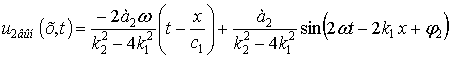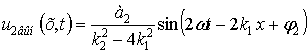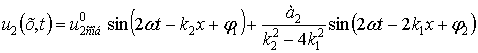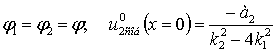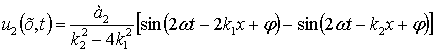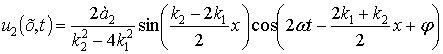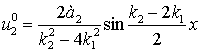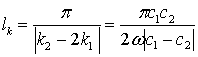