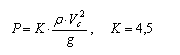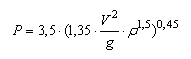ТЕХНИЧЕСКИЕ НАУКИ /10.Горное дело.

С.К.Молжигитов

Казахский национальный технический университет имени К.Сатпаева. Казахстан, Алматы

ОЦЕНКА УДАРНОЙ НАГРУЗКИ СЕЛЕВОГО ПОТОКА НА ПОПЕРЕЧНУЮ ЖЕСТКУЮ ПРЕГРАДУ

На основе результатов экспериментальных исследований воздействия селевого потока на поперечную жесткую преграду в виде глухой стены а, также учета газовой компоненты селя проводится оценка верхнего предела ударной нагрузки селя на противоселевые сооружения. В основу расчета нагрузки от селя многими исследователями берется принцип гидродинамическое давление обтекания преграды струей. Этот принцип положен в основу вывода формул С.М.Амирджанова, У.Р.Мирза-заде [1], Г.М.Беручашвили /6/, Херхеулидзе, Сохадзе и других исследователей.

Приведем известные формулы расчета нагрузки селя на поперечную глухую преграду:

Формулы расчета давления
ГрузНИИГиМ
Ржевский Б.Н., Нечаев Н.Ф.
Херхеулидзе И.И.
Гонора А.Л., Пик-Пичака Е.Г.	с-скорость звука в среде

ρ- плотность селя, кг/м³; V- скорость селя, м/с; α-процентное содержание воздуха в водонасыщенном грунте (сель), меняется в пределах 0÷0,04.

В формуле расчета ГрузНИИГиМ коэффициент К определен экспериментально на лабораторной установке в диапазоне изменения скоростей течения селя от 1,5 до 4,3 м/с, глубин потока от 4 до 1О см. Суммарное давление селя на плоский щит (преграду высотой 30 см) измерялось динамометром и тензодагчиками.

Приведем сравнительные графики этих формул.

Как видим приведенные формулы расчета не превышают определенного предела, например, при 6 м/с формулы расчета А.И.Квасова и Б.Н.Ржевского, Н.Ф.Нечаева примерно совпадают и выдают значение 5,8 кг/см². Данные значения получены в лабораторных условиях. Недостаточно обоснованы перенос этих значении на натурные масштабы. В этих формулах фигурируют только два параметра, это скорость и плотность селевого потока, т.е. давление выражается в виде P=f(ρ,V). На наш взгляд значения этих формул недостаточно отражают реальные давления оказываемые селевыми потоками на преграды. Как известно ранее приведенные формулы обоснованы на известной формуле гидравлического сопротивления потоку:

Где с – коэффициент зависящий от формы тела, А – площадь найбольшего сечения тела, перпендикулярный перпендикулярной направлению потока, ρ – плотность текущей жидкости (газа), V – относительная скорость движения тела в среде. Данная формула используется в гидродинамике для расчета гидравлического сопротивления тела потоку в однородной среде, в то время как сель является многокомпонентной средой.

Селевые потоки 1973 г. на р. М.Алматинка, 1975 и 1977 гг. на р.Б.Алматинка показали, что проблема динамического воздействия селя на преграду значительно сложнее, чем представляется теоретически. В 1977 г. на р.Б.Алматинка селем были разрушены опоры ЛЭП, водозаборы каскада ГЭС, кирпичные дома, причем нагрузки, которые способны были выдерживать эти разрушенные сооружения, в несколько раз превышали давления, подсчитанные по общеизвестным формулам обтекания. Ясно что, причиной разрушения этих сооружений явились импульсные нагрузки.

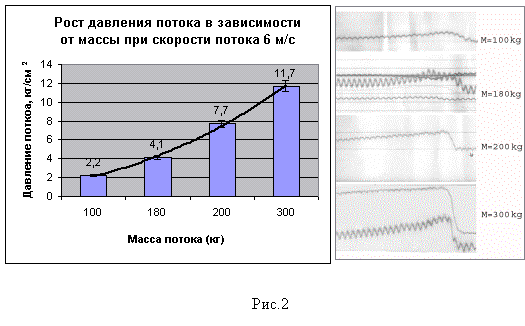
Результаты проведенных нами экспериментальных исследований в лабораторных условиях показали [2] зависимость нагрузки селя от массы потока. Также было выявлено, что максимальная нагрузка от удара селевого потока приходится на первые 50÷100 мсек времени воздействия потока. Учитывая высокую вязкость селевой массы необходимо констатировать большую погрешность модели обтекания тела потоком т.к. за короткое время удара сель не успевает изменить форму.

Как мы видим, давление возрастает не пропорционально относительно массы. Можно предположить что, это связано с волновым характером ударного процесса. При волновом процессе удара волна возмущений распространяется со скоростью звука от передней части селя на заднею часть. Таким образом, процесс нарастания давления а, также длительность воздействия селя является сложным процессом, который зависит как от скорости самого потока, так и от скорости распространения фронта возмущений внутри селевого потока. Также на характер воздействия потока на препятствие влияет скорость распространения возмущения внутри селя. Скорость звука внутри селя определяется физическими свойствами селевой массы. Как известно скорость звука в жидкостях определяется по формуле:

Где ν – коэффициент сжимаемости жидкости, ρ – плотность жидкости. Так как сель является многокомпонентной средой, то сжимаемость селя определяется не только водой но и другими компонентами. Также на сжимаемость селя влияет содержание воздуха и других газов. Влияние воздухосодержания на свойства водонасыщенного грунта не ограничивается увеличением или снижением его сжимаемости. Г.М,Ляхов [3] утверждает, что максимальное давление, скорость распространения максимума давления и другие параметры, волны существенно зависят от содержания воздуха α1 в водонасыщенном грунте. С возрастанием α1 от нуля до 0,04 максимальное давление убывает на два порядка, скорость максимума - более чем на порядок. При изменений содержания воздуха α1 от 0 до 0,01 а, скорость звука с в водонасыщенном грунте изменяется от 1620 до 26 м/с.

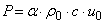
Приближенно оценить влияние воздухонасыщения на величину пиковых (ударных) нагрузок от селя на жесткое сооружение можно следующим образом; А.Л.Гонор и Е.Г.Пик-Пи-чак /24/ отмечают, что максимальные пиковые нагрузки от снежных лавин на твердую стенку находятся в хорошем соответствии с расчетом по одномерной теории гидравлического удара где α≤ 1 - поправочный коэффициент; ρ₀ - плотность жидкости; с - скорость распространения ударной волны; u₀ - скорость соударения жидкости с твердой стенкой.

Исходя из этого можно полагать, что график возрастания давлении (рис.2) ограничено сверху некой эффективной массой, которая определяется как M_e=ρ·s·c·Δτ, где ρ – плотность среды, s – площадь поперечного сечения потока, c – скорость звука в среде, Δτ – длительность нарастания пикового давления. По полученным осциллограммам были изучены длительности воздействия потока на стенд датчиков. Длительность нарастания давления от начала удара до максимального значения находилась в пределах 0,03÷0,09 сек в то время как длительность самого удара менялась в пределах 0,32÷0,38 сек. Исходя из положения, что сжимаемость грязекаменной среды сильно зависит от газовой компоненты и по последним оценкам скорость распространения возмущения в среде равно 300≤с≥600 м/c [4] мы можем определить верхний предел давления в полученных нами результатах. Длина распространения ударной волны L=600м/с·50·10^-3с=30 м. Отсюда эффективная масса равно

M_e=ρ·s·c·Δτ=2·10³ кг/м³·21·10^-2 м²·30 м =12600 кг,

что дает максимально возможное давление при предположении о линейной зависимости возрастания давления от массы в районе 500 кгс/см².

Таким образом мы предлагаем более сложную модель расчета нагрузки селевого потока на преграду. Которую можно представить в виде P=f(ρ,ν,M_е,V). Где ρ,ν –плотность и сжимаемость грязекаменной среды, M_е – эффективная масса, которая определяется скоростью распространения звука в потоке и площадью сечения потока. Предлагаемая нами модель позволяет переносить результаты лабораторных исследований на натурные масштабы, что являлось слабым местом предыдущих моделей расчета.

Литература

1. Амирджанов С.М., Мирза-заде У.Р. Вопросы расчета гидравлических параметров потока и установление устойчивости речных гидротехнических сооружений на селеносных реках Нуха-Закатальской зоны//Тр.АзНИИГиМ, 1966., Вып.6.С.199-217.
2. Байнатов Ж.Б., Молжигитов С.К., Тулебаев К.Р. Некоторые результаты экспериментального исследования динамики ударного воздействия селевого потока на сплошную среду.Вестник КаздорНИИ, №3-4(4), 2004.С.42-45.
3. Ляхов Г.М. Волны в грунтах и пористых многокомпонентных средах. М., 1982.288с.
4. Молжигитов С.К. Селевые потоки и влияние газовой компненты селя на динамику его воздействия на защитные сооружения. Наука и новые технологии. №7. 2012. Республиканский научно-теоретический журнал. Бишкек 2012. С.31-34