Механика
А.А. Танирбергенова
Карагандинский
государственный технический университет, Казахстан
МетОдика расчета надежности
механических
систем со случайными параметрами
Одним из важных проблем современной науки и техники
является обеспечение надежности и долговечности технических объектов. Основой
для этого служат комплекс мер, принимаемых на стадии проектирования,
изготовления, монтажа и эксплуатации. Среди этих мер особое место занимают
вопросы прогнозирования надежности механических систем на стадии проектирования,
решаемые на базе объединения методов механики деформированного твердого тела с
методами теории веоятностей и математической статистики.
Схема расчета надежности механических систем на стадии
проектирования приведена на рисунке 1, в число исходных данных для
проектирования кроме конструктивной схемы должна априорная информация или
статистические данные по изменчивости нагрузок, свойств материалов и системы.
На стадии проектирования назначают нормативные значения надежности 
. Выбор этого показателя представляет сложную технико –
экономическую проблему. При этом учитывают современное техническое состояние и
темпы научно – технического прогресса в данной отрасли, принятые в данное время
нормативные коэффициенты эффективности капитальных вложений и амортизационных
отчислений, стоимость материалов и комплектующих изделий и т.д.
На основе конструктивной схемы объекта проводится
геометрическая и физическая схематизация объекта и выделяется элементы
механической системы. После этого состовляется функциональная схема
взаимодействия элементов между собой. В этой схеме выделяются блоки
последовательно соединенных элементов, блоки параллельно соединенных элементов
(если имеются). Эти блоки могут образовать смешанное соединение или сложную
систему. Основным этапом прогнозировния надежности системы является расчет
надежности элемента конструкций (детали), схема которого приведена на рисунке 2.
Расчет надежности следует начать с выбора модели отказа.
При расчете надежности на основе статической модели отказ трактуется как
случайное событие, возникающее при достижении элементом конструкций предельного
состояния. В зависимости от эксплуатационных требований за предельное
состояниеможет быть принято начало появления пластических деформаций, хрупкого
разрушения, усталостных повреждений, достижение недопустимых перемещений или
критических нагрузок. Каждое предельное состояние характерезуется определенным
параметром 
(предельное
напряжение или перемещение, критическая нагрузка и т.д.), который может быть
детерминированной случайной величиной. В последнем случае на основе
статистических данных о свойствах материала необходимо определть плотность
распределения этого параметра 
или хотя бы его
математическое ожидание и дисперсию.
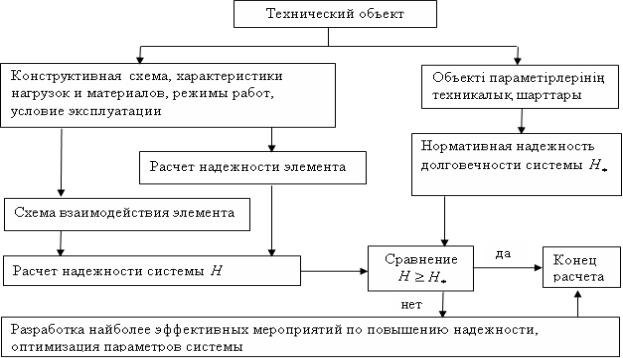
Рисунок 1 – Схема расчета надежности механической системы
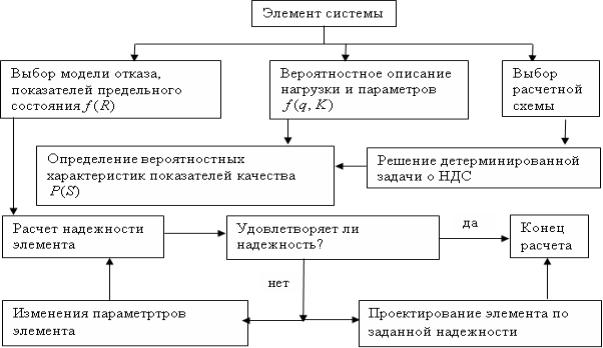
Рисунок 2 – Расчет надежности элемента
Следующим шагом является вероятностное описание нагрузок 
. Для этого надо иметь статистические данные об изменчивости
действующих нагрузок и условий работы. Далее должна быть проанализирована
изменчивость конструктивных параметров, каторая зависит от технологии
изготовления изделия и качества оборудования. Принятая система допусков
ограничивает рассеяние действительного размера около номинального. При
необходимости учета изменчивости конструктивного параметра его считают
случайной величиной, распределенной по нормальному закону с математическим
ожиданием, равным номинальному размеру и стандартом, равным одной треть допуска
на размер (правило «трех сигм»).
Выбор предельного состояния, вероятностное описание его
характеристик, нагрузок и параметров системы наряду с выбором расчетной схемы
является исходными данными для расчета надежности элемента конструкций. Чем
больше точность этих данных, тем больше достоверность вычисления надежности.
Непосредственный расчет надежности начинается с решения
детерминированной задачи о НДС конструкций. В результате решения
определяют зависимости между показателем качества состояния конструкций и ее
случайными параметрами. Показатель качества определяется характеристикой
предельного состояния – это напряжение, перемещение или нагрузка. При
аналитическом решени задачи получаем функциональную зависимость, а при
численном решении это связь определяется таблично или графически. В последнем
случаерезультаты расчетов необходимо представить в аналитическом виде,
используя методы регрессионного анализа. Для этой цели лучше использовать
методы рационального планирования экспериментов.
Полученная зависимость показателя качества от случайных
параметров системы позволяет определить вероятностные характеристики показателя
качества применением методов теории вероятностей. Конкретное использование этих
методов применительно к определению вероятностных характеристик расчетных
напряжений изложено в работе [1], где приведены точные и приближенные
методы, а в работе [2]
изложены методы определения этих характереистик. При численном
решении задачи используется метод статистического моделирования с выбором
функции распределения выходной величины.
Следующим этапом расчета является определение надежности
элемента. Для этой цели в общем случае используются выражения, приведенные в
работах [1,
3]. Для расчета надежности усталостному разрушению
используются соотношения, полученные в работе [4], а расчет
надежности при плоском напряженном состоянии проводится по методике изложенной
в [5], а оценка надежности гибких стержней проводится в работе [6].
Если вычисленная надежность приемлима, то на этом расчет
преращают. Если надежность не удовлетворяет, то меняют конструктивный параметр
элемента или его материала и расчет надежности повторяют до получения
приемлимого результата. В последнем случае вместо неоднократного изменения
параметров системы можно рекомендовать выбор конструктивного размера из условия
обеспечения приемлимого показателя надежности. Методика этого расчета изложена
ниже.
После определения надежности всех элементов производится
расчет надежности системы (технического объекта) в целом. Для этого
используются функциональная схема взаимодействия элементов и формулы, подходы,
приведенные в работе [7].
Далее расчетная надежность системы сравнивается с
нормативной надежностью объекта 
. Если она приемлимо больше 
, то на этом расчет прекращают. Если расчетная надежность
меньше нормативной, то принимают меры по повышению надежности системы.
К таким мерам относятся:
-
повышение надежности отдельных элементов путем изменения
конструктивных параметров или материала;
-
изменение схемы взаимодействия элементов путем
дублирования малонадежных элементов;
-
оптимизация параметров системы по надежности.
Оптимизационные расчеты проводятся по методике,
изложенной в статье [8]
и заключаются в определении надежности элементов,
обеспечивающих нормативную надежность системы при минимальных затратах. Далее
по найденным надежностям элементов определяются их параметры.
При проектировании элементов конструкций и деталей машин
с случайными параметрами возникает задача определения характеристик элемента из
условия обеспечения заданной надежности. Эта же задача возникает и при
проведении оптимизационных расчетов. Методика такого расчета изложена в работах
[1, 9].
Из анализа этих соотношении видно, что не всегда можно
получить аналитическую зависимость геометрического параметра 
от показателя
надежности. В этих случаях рекомендуется численно построить график зависимости
надежности от искомого конструкивного параметра. Далее по заданной надежности
из графика легко можно определить конструкивный параметр.
Иногда проектный расчет проводится методом
послеовательных приближении. В этом случае за начальные приближение
рекомендуется брать размер, полченный из прочностного расчета по допускаемым
напряжениям. Причем, нормативный коэффициент запаса можно брать по заданной
надежности с учетом случайной изменчивости вероятностные характеристик
нагружения и материала. Необходимые для этого соотношения приведены в работе [1].
Список литературы
1.Бакиров Ж.Б. Вероятностные методы расчета элементов
конструкций. Учебное пособие. Караганды: КарГТУ, 2000. – 185с.
2.Бакиров Ж.Б., Танирбергенова А.А. Автоматизация численного
расчета вероятностных характеристик напряжений. //
Научный вестник НГТУ Новосибирск, №3 (48) 2012.
3.Бакиров Ж.Б., Танирбергенова А.А. Расчет
надежности деталей машин по усталостному разрушению. // Труды междунар. науч.
конфер. «Наука
и образование – ведущий фактор стратегии «Казахстан 2030». –Караганда, 2010.
4. Бакиров
Ж.Б., Танирбергенова А.А. Автоматизация численного расчета вероятностных характеристик
напряжений. // Наука и образование Южного Казахстана. – Шымкент, 2010. –
№4.
5. Бакиров Ж.Б. Расчет надежности
конструкции при случайных компонентах напряжений. //Известия ЕврНУ. Серия техн.
Науки, №1.–Астана, 2001–С42-46.
6. Бакиров Ж.Б. Расчет надежности сжатых
гибких стержней. // Труды университета. Вып. 1. Караганды:
КарГТУ, 2004.
7. Бакиров Ж.Б., Танирбергенова А.А. Расчет надежности многоэлементных
систем на основе статических модулей. // Материали за VIІ международна научнапрактична
конференция «Ключови въпроси в съвременната наука 2011» Том 38, Технологии. -
София, 2011.
8. Бакиров Ж.Б., Танирбергенова А.А. Оптимизация конструкций по надежности // Материалы
IX международной научно – практической конференций «Европейская наука ХХI
века – 2013» Том 29, Техническая наука. – 7-15 мая 2013, Przemys1l, Nauka
i studia 2013.
9. Бакиров Ж.Б., Танирбергенова А.А. Проектирование элементов
конструкций заданной надежности. // Труды междунар. науч. конфер. «Казахстан
2030» Караганда, 2005.