DSc. L'vov A.A., PhD L'vov P.A., and Matoshko
I.M.
Saratov State Technical University named after
Gagarin J.A., Saratov, Russia
Optimization of a multi-probe
transmission line reflectometer
At present two basic techniques are used for automatic measurements of
microwave circuit parameters.
The measurement
technique with a multi-probe transmission line reflectometer (MTLR) is
well-proved. It relies upon the
analysis of distribution of a standing wave inside the line being dependent on
complex reflection coefficient (CRC) of an attached load under test and
absolute value of incident wave complex amplitude. Thus, it seems quite natural to use MTLR with three probes to obtain
the estimates of unknown parameters.
Usually, additional probes are used in order to enlarge the measurement
wavelength range [1].
From one hand, the
increase in the number of measuring probes allows one to exclude dramatically
the influence of random noise on measurement accuracy [2] and to raise the
precision of calibration as well [3].
But from the other hand, the considerable growth of probe's number may
cause the appreciable distortion of standing wave pattern in the line due to
own reflections of detectors. The
unpredictable systematic errors being brought about by this reason shade the
evident merit of MTLR: the simplicity of its construction.
Therefore, the
problem is reduced to a trade-off of keeping random errors to a minimum against
rising of systematic errors. Such a
compromise may be achieved by use of MTLR with the limited number of measuring
probes. The improvement of MTLR
accuracy can be attained by means of optimization of its parameters at the
development stage [4].
There is one more
difficulty to be considered. Bearing in
mind that optimization of MTLR parameters takes place before the particular
detectors are attached to probes it is impossible to allow for the errors
caused by probe (detector) gains. The
authors called this source of errors 'a probe gain effect' and suggested to
make up for a loss in accuracy using the effective methods of control of measurement
process at the stage of ANA operation.
The paper describes
parameter MTLR optimization for measurements in both narrow and wide frequency
ranges and the original technique for reduction of errors due to probe gain
effect by means of optimal control of measurement process.
The general MTL can
be a segment of a microwave tract with regular cross-sections. Measurement probes with square-law detectors
are arranged lengthwise being severe coupled with the electromagnetic field
inside not to bring about the disturbances of its pattern.
The mathematical
model of MTLR is well-known [1-3]:
uj = aj b 2 {1 +r2 +2r [cosj cos(4pdj
/l) + sinj sin(4pdj /l)] } + xj , ![]() (1)
(1)
Here uj
is a signal reading measured at the j-th probe, b is an unknown complex amplitude of standing wave in the line, aj
is the j-th probe's gain, dj is the distance from the
flange of load under test to the j-th probe, xj is a measurement error, l is a wavelength in the MTL, r and j are
modulus and phase of termination under test, N is the number of probes. The parameters dj and l always assumed
to be exactly known.
The
conventional variable substitution makes this system linear with respect to new
intermediate variables qi
uj = q1 x1j + q2 x2j + q3 x3j + xj, ![]() , (2)
, (2)
where
q1 = b2(1
+r2), q2
= b2r×cosj, q3
= b2r×sinj, (3)
x1j = aj, x2j = 2aj×cos(4pdj /l),
x3j = 2aj×sin(4pdj /l),
![]() . (4)
. (4)
As a rule, the errors xj are induced due to the shot noise of the
probe detectors and thermal noise of the amplifiers. Therefore, they may be
considered as an independent sample of a stationary normal random process with
zero mathematical expectation and fixed variances ![]() . Thus, it is
reasonable to use the maximum likelihood (ML) method [2] to obtain efficient
estimators of vector
. Thus, it is
reasonable to use the maximum likelihood (ML) method [2] to obtain efficient
estimators of vector ![]() = (q1, q2, q3)T (3). In this event
estimation accuracy of
= (q1, q2, q3)T (3). In this event
estimation accuracy of ![]() is usually
characterized by the variance matrix of estimates of these coefficients (or
error matrix) [2], given by equation (5), where: yj = 4pdj /l are phases and
is usually
characterized by the variance matrix of estimates of these coefficients (or
error matrix) [2], given by equation (5), where: yj = 4pdj /l are phases and ![]() are measurement weights;
are measurement weights; ![]() is an unknown coefficient;
–1 is the designation of an inverse matrix.
is an unknown coefficient;
–1 is the designation of an inverse matrix.
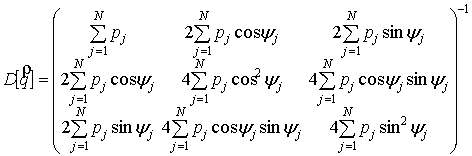 , (5)
, (5)
The
accuracy of unknown parameters in the set (1) is entirely determined by the accuracy
of intermediate parameters q1,
q2, q3. Furthermore,
it is necessary to know the estimates of all the components to obtain the
estimators of b, r, and j. In this case the theory advises to minimize
the determinant of matrix D[![]() ] called the generalized variance of estimated parameters.
] called the generalized variance of estimated parameters.
As it
can be seen from (5) the matrix D[![]() ] depends on parameters of MTLR dj and pj . As it mentioned above, coefficients pj are unknown at the development
stage. Hence the optimization of MTLR
can be performed only by virtue of appropriate selection of probe arrangement.
] depends on parameters of MTLR dj and pj . As it mentioned above, coefficients pj are unknown at the development
stage. Hence the optimization of MTLR
can be performed only by virtue of appropriate selection of probe arrangement.
It is evident that the choice of dj (or yj) minimizing the
determinant of D[![]() ] at the same time maximizes the one for inverse matrix D–1[
] at the same time maximizes the one for inverse matrix D–1[![]() ]. The problem of
determinant D½D-1[
]. The problem of
determinant D½D-1[![]() ]êof matrix D–1[
]êof matrix D–1[![]() ] maximization is more convenient and easy.
] maximization is more convenient and easy.
As a
trivial corollary of the Hadamard's inequality one can obtain a result that
determinant D½D–1[![]() ]ê runs into maximum if the matrix D–1[
]ê runs into maximum if the matrix D–1[![]() ] is diagonal, the maximum value being easily calculated
] is diagonal, the maximum value being easily calculated
Dmax = 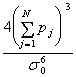 (6)
(6)
Hence the minimum value of determinant of
error matrix D[![]() ] is
] is
Dmin = ![]() =
= ![]() (7)
(7)
where ![]() is the volume of
error dispersion ellipsoid for simultaneously efficient estimator of vector
is the volume of
error dispersion ellipsoid for simultaneously efficient estimator of vector ![]() . The expression (7) determines the potentially achievable
accuracy of measurements by MTLR method at fixed wavelength.
. The expression (7) determines the potentially achievable
accuracy of measurements by MTLR method at fixed wavelength.
If it is
necessary to measure with the utmost accuracy parameters of microwave circuits
in narrow wavelength range in the vicinity of central point l0 one should minimize the generalized variance of
intermediate variables (3). The probe
arrangement resulted from that procedure coincides with D-optimal experiment
design. In accordance with the previous
discussion and expression (5) the following set of equalities has to be true
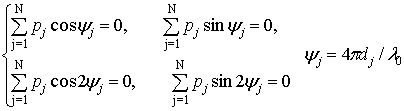 (8)
(8)
Since
all pj are unknown at the
development stage it seems quite natural to assume them being equal. Then every selection of distances dj satisfying (8) provides
the optimal estimation of load under test CRC at the wavelength l0. For example,
the next equidistant probe arrangement meets the stated requirements
![]() (9)
(9)
where N³3; k is an integer; N/2 being non-multiple of k.
The
expression (9) allows a convenient arrangement of MTLR probes to be found by
proper choice of parameter k. Of course
there may be the other different probes' arrangements exhibiting the same
quality, but they can not improve the measurement accuracy of MTLR having
parameters dj been chosen
in accordance with (9).
Unfortunately,
it is impossible to measure with potentially achievable accuracy at every wavelength
from the wide continuous range [lmin, lmax] by means of suitable selection of MTLR
probes' arrangement. Moreover, the
determinant of error matrix can not reveal the optimal properties of MTLR in
the range because it may be calculated only for the fixed wavelength. Hereby, it is necessary to use the optimization
criterion suitable for the problem occurred.
One of the effective characterizations of MTLR accuracy
may be an efficiency function (EF) of estimates [4] ![]() . It represents the
ratio of error matrix determinant of parameters
. It represents the
ratio of error matrix determinant of parameters ![]() for current values of
dj and pj to the one for joint
efficient estimator of the same parameters at any specified wavelength l from the range [lmin, lmax]. I.e. this function is the squared fraction where numerator
is dispersion ellipsoid volume for current arrangement of probes and weights
and denominator is one for the optimal values of dj, pj
at given wavelength l. It is evident that always
for current values of
dj and pj to the one for joint
efficient estimator of the same parameters at any specified wavelength l from the range [lmin, lmax]. I.e. this function is the squared fraction where numerator
is dispersion ellipsoid volume for current arrangement of probes and weights
and denominator is one for the optimal values of dj, pj
at given wavelength l. It is evident that always ![]() ³1.
³1.
The
weights pj are still
implied to be equal. So one should minimize
the EF uniformly in the wave range [lmin, lmax] by means of appropriate selection of distances dj from tested load flange
to probes. That problem could be formulated
as follows
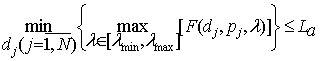 (10)
(10)
where La
is assured level of estimation accuracy at any arbitrary wavelength from
the fixed range. The solution of (10)
is rather difficult due to its nonlinearity.
Therefore, only numerical techniques can provide the successful
decision.
The authors developed the software for computer-aided
design (CAD) of MTLR based on the minimax search of function (10). It can work in three different modes
corresponding to probable formulations of optimization problem. The first statement consists in finding of
the largest range (i.e. lmin and lmax) when the number of probes N is given. The basic data for the second mode are given wavelength range [lmin, lmax] and fixed N, maximum accuracy of measurements being to achieved uniformly in
the whole range. Here one more
relationship is added to (10)
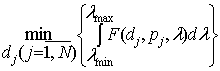 (11)
(11)
The last mode consists in determination of minimal
required number of probes to provide the measurements in the fixed range with
given accuracy La. The decision of all the problems is performed
by suitable selection of probes' arrangement.
As a rule, La £ 1.5.
User friendly software operates in a form of a
dialogue. Output data contains the
distances from the load flange of MTLR to probes and the plot of ![]() versus l for the best probes'
arrangement. Some effective
arrangements of the limited number of MTLR probes were found. The EF plot of 8-probe TLR is shown on
Fig.1. The measurement frequency (or
wavelength) range (B) is near to 6 octaves.
versus l for the best probes'
arrangement. Some effective
arrangements of the limited number of MTLR probes were found. The EF plot of 8-probe TLR is shown on
Fig.1. The measurement frequency (or
wavelength) range (B) is near to 6 octaves.
Since
the fractional change in efficiency function does not exceed 1.5 inside the
required wavelength range the corresponding spread in values of the estimates
of intermediate variable q1,
q2, q3 will not be 7% higher than that for simultaneously
efficient estimator.
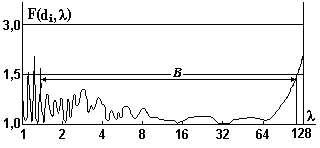
Fig. 1. Dependence
of efficiency function on wavelength given in relative units.
But such
accuracy may be insufficient if it is necessary to develop wide band ANA of
high precision. Moreover, the EF
depends upon weights pj either. After the probe gains aj are found during the calibration of MTLR
the derived weights may change ![]() making it higher than
La for some wavelengths
from the range [lmin, lmax] and rising the estimation errors.
making it higher than
La for some wavelengths
from the range [lmin, lmax] and rising the estimation errors.
The
noticed difficulties can be overcome if sequential sampling of probe detector
responses is used. That way of the output data collection is rather
widespread because of relatively small volume of hardware required. As it can be seen from (8) the error matrix
and efficiency function depend on variances of noise errors ![]() defining a
signal-to-noise ratio of probe output.
It is well-known that the noise variance is reciprocally proportional to
accumulation time of the detector output signal. Thus, one can vary the values of weights pj adjusting the integration times of probes' responses.
That makes possible to compensate the influence of probe gains on measurement
accuracy and provide high precision of measurement at every wavelength from the
range.
defining a
signal-to-noise ratio of probe output.
It is well-known that the noise variance is reciprocally proportional to
accumulation time of the detector output signal. Thus, one can vary the values of weights pj adjusting the integration times of probes' responses.
That makes possible to compensate the influence of probe gains on measurement
accuracy and provide high precision of measurement at every wavelength from the
range.
Actually,
if all dj and pj are given (after
calibration procedure has been performed) the relationships (8) may not be true
for arbitrary l from the fixed range. But the appropriate fitting of weights pj enables to make up for
discrepancies caused by the probe gain effect.
Therefore, at every measuring wavelength the redistribution of
accumulation times of probe responses is to be made, the total measurement time
being constant. It can be easily done using the solution of linear set (8) for
unknown variables pj, but
one more equation defining the constrain for the total time of measurements
should be added
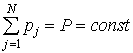 (12)
(12)
Knowing
relative pj one can
calculate the corresponding accumulation times to be established. From the physical point of view it is
necessary to increase the integration times for 'successfully' arranged probes
(closely to potential loops of the standing wave with period l) and to decrease them for 'badly' arranged
probes (near the standing wave nodes).
 The authors developed the software package
for automatic control of the process of measurements with MTLR. It calculates the required accumulation
times of probes' responses depending on the particular wavelength l and given dj , aj. It should be
noticed that the control technique described permits one to measure the CRC of
attached loads under test with practically potentially achievable accuracy at
every fixed frequency from the defined range.
The adjustment of weights pj
in accordance with solution of the set (8), (12) makes the error matrix D[
The authors developed the software package
for automatic control of the process of measurements with MTLR. It calculates the required accumulation
times of probes' responses depending on the particular wavelength l and given dj , aj. It should be
noticed that the control technique described permits one to measure the CRC of
attached loads under test with practically potentially achievable accuracy at
every fixed frequency from the defined range.
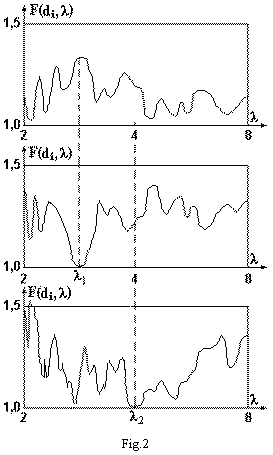
The adjustment of weights pj
in accordance with solution of the set (8), (12) makes the error matrix D[![]() ] diagonal and hence the EF becomes equal to
unity. It can be illustrated from Fig.2
where one can see the EF for the same MTLR (only small part of the whole wavelength
range is shown). The upper curve shows the EF calculated for all pj = 1 and the
other curves show the same EF, but with the fitted times of integration for the
wavelengths l1 = 2,5 (middle plot) and l2 = 4,0 (lower plot) respectively. It can be seen from the plots that measuring
accuracy becomes higher for the fixed wavelengths from the range due to
appropriate control of measurements by variation of detectors' accumulation
times.
] diagonal and hence the EF becomes equal to
unity. It can be illustrated from Fig.2
where one can see the EF for the same MTLR (only small part of the whole wavelength
range is shown). The upper curve shows the EF calculated for all pj = 1 and the
other curves show the same EF, but with the fitted times of integration for the
wavelengths l1 = 2,5 (middle plot) and l2 = 4,0 (lower plot) respectively. It can be seen from the plots that measuring
accuracy becomes higher for the fixed wavelengths from the range due to
appropriate control of measurements by variation of detectors' accumulation
times.
The
suggested technique for optimization of MTLR parameters allows the efficient
estimates of load under test CRC to be obtained both in narrow and wide wavelength
ranges. It was implemented by software package for computer in the form of CAD
system of ANAs based on MTLR. The use
of specified software in practice helped to develop the 8-probe TLR operating
in the frequency range [0.5, 96] GHz (microstrip version). From the other hand the arrangement of probes in
accordance with (9) enables one to measure with potentially achievable accuracy
in narrow wavelength range.
The implementation of optimal control of measurement
process may be useful in wide wavelength range ANAs and narrow range ones as
well since it eliminates the probe gain effect. The corresponding software being developed improved dramatically
the performance of 8-probe TLR in the whole frequency range mentioned above.
Finally, the use of MTLR having the limited number of
optimally arranged probes (N£10) in combination with optimal
calibration and data processing techniques can raise considerably the accuracy
of wide frequency range ANA. Bearing
in mind the cheapness and simplicity of MTLR it should be notified that
manufacturing cost of wide band ANAs based on considered technique can be
reduced drastically in comparison with nowadays vector ANAs without any loss in
accuracy of measurements.
REFERENCES
1. R.
Coldecott, "The Generalized Multiprobe Reflectometer and its Application
to Automated Transmission Line Measurements", IEEE Transactions on
Antennas and Propagation, vol. AP-21, no. 4, pp. 550-554, April, 1973.
2. A.A. L'vov, A.A. Mouchkaev, K.V. Semenov,
“Accuracy Improvement of the Automatic Multiprobe Transmission Line
Reflectometer”, The Automatic RF Techniques Group Conference Digest, ARFTG
47th, San Francisco, U.S.A., pp. 196-202.
3. A.A.
L'vov and K.V. Semenov, “A Statistical Calibration Technique of the Automated
Multiprobe Transmission Line Reflectometer” – Proceedings of the 10th International
Conference “Systems for Automation of Engineering and Research”, September
27–29, 1996, St. Konstantin, Bulgaria, pp. 38-42.
4. B.M.
Katz, A.A. L’vov, V.P. Meschanov, E.M. Shatalov, L.V. Shilova, “Synthesis of a
Wideband Multiprobe Reflectometer”, IEEE Transactions on Microwave Theory and
Techniques, Vol. 56, No. 2, February, 2008, P. 507-514.