Тлеубаева Г.С., Бердалиева Г.А.

ЮКГУ им. М.Ауезова, Шымкент, Казахстан

Некоторые задачи распознавания образов

Проблема распознавания в течение достаточно продолжительного времени привлекает внимание специалистов в области прикладной математики, а затем и информатики. Центральная задача распознавания образов построение на основе систематических теоретических и экспериментальных исследований эффективных вычислительных средств для отнесения формализованных описаний ситуаций и объектов к соответствующим классам. В основе такого отнесения лежит получение некоторой агрегированной оценки ситуации, исходя из ее описания. При условии установления соответствия между классами эквивалентности, заданными на множестве объектов распознавания, автоматизация процедур распознавания становится элементом автоматизации процессов принятия решений.

Становление распознавания служит отличной моделью развития математической теории обработки и преобразования информации, развития, в процессе которого эвристические методы получают строгое обоснование и начинают применяться в рамках вполне формализованных регулярных процедур. Само распознавание является достаточно разработанным вариантом такой теории, поскольку позволяет разрешать ее основную задачу – синтезировать и выбирать алгоритмические средства для извлечения полезной информации из данных.

К постановке задачи распознавания прибегают в тех случаях, когда трудно строить формальные теории и применять математические методы, что происходит обычно по двум причинам:

а) уровень формализации соответствующей предметной области или доступная информация таковы, что не могут составить основу для синтеза математической модели, отвечающей классическим математическим или математико-физическим канонам и допускающей изучение классическими аналитическими или численными методами;

б) математическая модель в принципе может быть построена, однако ее синтез или изучение связаны с такими затратами, что они существенно превышают выигрыш, приносимый искомым решением, либо выходят за пределы существующих технических возможностей, либо делают решение задачи просто бессмысленным. «Двойственность» распознавания проявилась в том, что решение таких задач ввело в обиход большое число эвристических алгоритмов. Довольно долго подавляющее большинство приложений теории распознавания было связано с плохо формализованными областями – медициной, геологией, социологией, химией и т.д. В этих областях еще трудно строить формальные теории и применять стандартные математические методы. В лучшем случае удается дать математическое оформление некоторым интуитивным принципам и затем применять полученные «эмпирические формализмы» для решения частных задач. При исследовании задачи или класса задач на базе так называемых «правдоподобных» рассуждений предлагался нестрогий, но содержательно разумный метод решения и основанный на нем алгоритм; обоснование же производилось непосредственно в эксперименте с задачами. Алгоритмы, выдержавшие подобную экспериментальную проверку, т.е. приносившие успех при решении определенных практических задач, применяются, несмотря на отсутствие математических обоснований. Второй этап развития теории распознавания отличался попытками ставить и решать задачу выбора в конкретной ситуации наилучшего в некотором смысле алгоритма и попытками переходить от описания отдельных некорректных алгоритмов к описанию принципов их формирования, т.е. попытками строить единообразные описания для множеств эвристических, но успешно решающих реальные задачи.

Потребность в синтезе моделей алгоритмов распознавания в первую очередь определялось необходимостью фиксировать каким-то образом класс алгоритмов при выборе оптимальной или хотя бы приемлемой процедуры решения конкретной задачи. В свою очередь, попытки построения таких моделей породили интерес к собственно «математическим» свойствам алгоритмов распознавания, в особенности их строгого обоснования. Оказалось, что получение описания класса алгоритмов распознавания представляют собой задачу, сходную с построением классического определения алгоритма.

Изучение моделей распознающих алгоритмов позволило получать интересные теоретические результаты и решать разнообразные прикладные задачи. Вместе с тем данному методу решения задач распознавания присущи и некоторые серьезные недостатки, которые не могут быть устранены при рассмотрении лишь отдельных моделей. Для преодоления этих трудностей была предложена общая теория распознающих алгоритмов, построенная на основе алгебраического подхода к решению задач распознавания, обеспечивающего эффективное исследование и конструктивное описание класса алгоритмов распознавания и предусматривающего введение такого определения алгоритма распознавания, в рамки которого укладываются все существующие модели алгоритмов.

Алгебраический подход предусматривает обогащение исходных эвристических семейств алгоритмов при помощи алгебраических операций и построение семейства, гарантирующего получение корректного алгоритма, обеспечивающего решение изучаемого класса задач. В его основе лежит идея индуктивного порождения математических объектов посредством обобщенного индуктивного определения. Выделяются базисные алгоритмы и модели распознавания и вводятся операции над ними, позволяющие последовательно порождать новые алгоритмы и модели. Выясняются условия, при которых данное семейство алгоритмов является базисным относительно выведенных операций, а также свойства, которыми должна обладать модель для того, чтобы в ней нашелся алгоритм, правильно классифицирующий все объекты произвольной конечной выборки. Формируются методы построения таких алгоритмов.

В алгебраическом подходе существенно используются особенности структуры, свойственные любой процедуре распознавания. Он предусматривает введение так называемого пространства оценок, промежуточного по отношению к исходным описаниям и допустимым ответам. Алгоритм распознавания при этом рассматривается как суперпозиция двух операторов. Первый из этих операторов – распознающий – в качестве ответов формирует элементы, называемые оценками, а второй – по оценкам определяет окончательные ответы.

Методология распознавания используется в информатике в двух качествах:

§ во-первых, по прямому назначению для решения задач распознавания в классическом смысле;

§ во-вторых, как средство точного исследования плохо определенных задач.

В последнем случае эта методология реализовывается приблизительно следующим образом. Пусть, например, имеются некоторые данные, полученные в результате физического или имитационного эксперимента. Эти данные в некотором весьма ограниченном смысле характеризуют изучаемые объект или явление; необходимо их воедино с тем, чтобы установить, какие закономерности отражаются в имеющемся материале. Для этого выдвигается некоторая простая гипотеза, которой придается математический облик, и делается попытка «объяснить» имеющийся материал с ее помощью. Последовательное использование ряда эвристик может позволить угадать модель. В противном случае происходит переход к поиску оптимального эвристического принципа – модели. Если оказывается, что соответствующего принципа не существует или им нельзя практически воспользоваться, то следует формировать некоторый конгломерат принципов, обеспечивающий выделение «федеративного» принципа; именно этот верхний уровень и соответствует возможностям и назначению алгебраического подхода.

Любому специалисту в своей практической деятельности приходится изучать зависимости между различными параметрами исследуемых объектов, процессов и систем. Из всех способов задания зависимостей наиболее удобным является аналитический способ задания зависимости. Однако, на практике специалист чаще всего получает зависимости между исследуемыми параметрами экспериментально. В этом случае ставится натурный эксперимент, изменяются значения параметров на входе системы, изменяются значения параметров на выходе системы. Результаты измерения заносятся в таблицу. В результате проведения натурного эксперимента получаем зависимости между исследуемыми параметрами в виде таблицы, т.е. получаем, так называемую, табличную функцию. Задача, возникающая перед исследователем, состоит в отыскании соответствующего аналитического выражения для функции, т.е. распознать табличную функцию. Для этой цели могут быть употреблены тригонометрические ряды, поскольку есть уверенность, что эта функция приближенно и достаточно точно может быть выражена суммой конечного числа первых членов ее ряда Фурье. Весь вопрос заключается в нахождении коэффициентов Фурье функции.

Пусть в интервале задана функция . Мы считаем, что при любом задании функции график ее нам известен. При этом в случае необходимости систему координат Оху следует параллельным сдвигом перенести так, чтобы весь график был расположен над осью Ох и как можно ближе к ней (рис. 1). Это скажется только на свободном члене разложении Фурье, а вместе с тем позволит избежать как отрицательных, так и слишком больших положительных значений функции.

Приближенное представление функции в виде многочлена Фурье требует отыскания первых коэффициентов Фурье

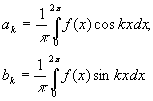
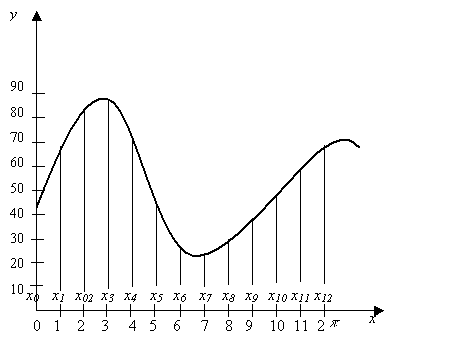
Рис. 1.

Приведем алгоритм решения задачи.

1. Задается функция в интервале .

2. Интервал делится на п равных частей с помощью точек .

3. Вводятся значения входных параметров (x_i , y_i)

4. Вычисляются коэффициенты a_k,,b_k

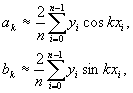
где .

5. Получаем приближенное выражение функции в виде тригонометрического многочлена

Принимая во внимание особенности множителей coskx_i и sinkx_i, берут п чаще всего равным 12 или 24. Мы здесь возьмем п=12.

x_i	0	1	2	3	4	5	6	7	8	9	10	11
y_i	44	46	76	88	86	63	24	20	26	40	58	65

Вычисляем коэффициенты a_k,,b_k_..

Так как соs0=1

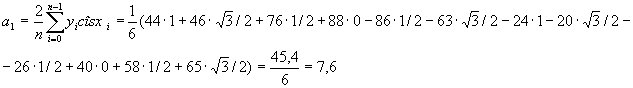
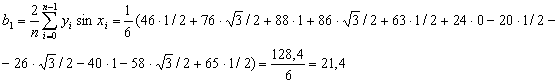
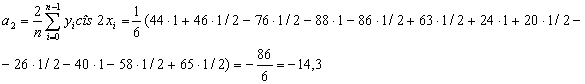
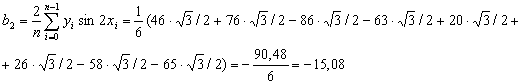
Таким образом, получаем приближенное выражение функции в виде тригонометрического многочлена второго порядка

Литература

1. Распознавание, классификация прогноз. Математические методы и их применение. – М.: Наука, 1989 г.

2. Горелик А.Л., Гуревич И.Б., Скрипкин В.А. Современное состояние проблемы распознавания

3. Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа. – М.: Наука, 1971г.