Заметим, что данная рекурсивная процедура включает в
себя рекурсивную поточечную оценку (12). Процедура (16) инициализируется вектором 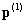 , который является оценкой первой точки
, который является оценкой первой точки 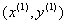 . Эта оценка может быть определена из исходных опытных
данных, из граничных условий или как априорная информация.
. Эта оценка может быть определена из исходных опытных
данных, из граничных условий или как априорная информация.
Представленный
алгоритм решает две важные задачи: подавление шумов и восстановление
непрерывной полной фазы. Проделанные эксперименты показывают, что точность
алгоритма высока при условии, что разница между значениями полной фазы в двух
соседних точках не больше чем 0.5 ÷ 1 радиан. Точность алгоритма тем
выше, чем меньше данная разница, даже при высоком уровне случайного шума.
Размер окна 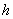 является ключевым параметром в точности
оценки фазы. Когда размер окна мал, локальная аппроксимация дает хорошее
гладкое приближение фазы, но чем меньшее измерений используется, тем более
чувствительна оценка относительно шума. Наилучший выбор параметра
является ключевым параметром в точности
оценки фазы. Когда размер окна мал, локальная аппроксимация дает хорошее
гладкое приближение фазы, но чем меньшее измерений используется, тем более
чувствительна оценка относительно шума. Наилучший выбор параметра 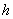 сводится к компромису между смещением и
дисперсией, которые зависят от степени многочленов в ЛАМ, дисперсии шума и
производных фазы порядка зависящего от использованной степени многочленов в
ЛАМ.
сводится к компромису между смещением и
дисперсией, которые зависят от степени многочленов в ЛАМ, дисперсии шума и
производных фазы порядка зависящего от использованной степени многочленов в
ЛАМ.
Теоретический анализ и эксперименты
показывают, что эффективность оценки локальной аппроксимации может быть
существенно улучшена при правильном выборе размера окна 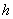 . Окно может быть переменным или постоянным, но должно быть
правильно выбрано.
. Окно может быть переменным или постоянным, но должно быть
правильно выбрано.
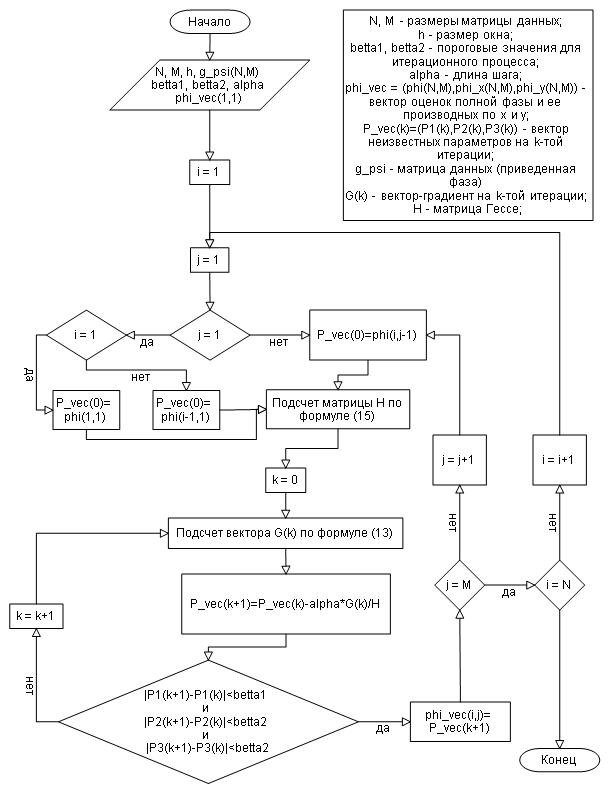
Рис. 2. Блок схема алгоритма.
3.
Результаты экспериментов: Для
сравнения эффективности работы разработанного алгоритма были использованы
результаты полученные от 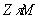 алгоритма, который считается одним из лучших алгоритмов по
восстановлению фазы, разработанных для данных содержащих шум [11]. Для оценки
точности алгоритмов была использована среднеквадратическая ошибка
алгоритма, который считается одним из лучших алгоритмов по
восстановлению фазы, разработанных для данных содержащих шум [11]. Для оценки
точности алгоритмов была использована среднеквадратическая ошибка 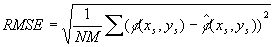 . В ЛАМ использовалось
прямоугольноe окнo
. В ЛАМ использовалось
прямоугольноe окнo 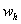 определенное на
целочисленной сетке
определенное на
целочисленной сетке 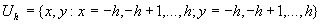 .
.
На Рис. 3 приведен пример исходной полной
фазы 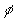 (а) и приведенной зашумленной фазы
(а) и приведенной зашумленной фазы 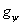 (б) полученной из
(б) полученной из 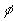 по формуле (5), при значении
среднеквадратического отклонения Гауссовского белого шума
по формуле (5), при значении
среднеквадратического отклонения Гауссовского белого шума 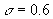 . На рис. 3 также приведены результаты восстановления для
различных значений размера окна (в)-(е). При сравнении исходной и
восстановленной фаз можно заключить, что подавление шумов и восстановление
произведено довольно точно.
. На рис. 3 также приведены результаты восстановления для
различных значений размера окна (в)-(е). При сравнении исходной и
восстановленной фаз можно заключить, что подавление шумов и восстановление
произведено довольно точно.
В таблице представленной ниже приведены
результаты оценки точности алгоритмов ПАФ и 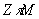 для исходной полной фазы
для исходной полной фазы 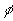 представленной на Рис.3 (а). Для оценки были
использованы разные размеры окна
представленной на Рис.3 (а). Для оценки были
использованы разные размеры окна 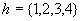 и разные значения
среднеквадратического отклонения (
и разные значения
среднеквадратического отклонения (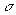 ) Гауссовского белого шума в (4).
) Гауссовского белого шума в (4).
|
Алгоритм/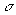
|
0.1
|
0.2
|
0.3
|
0.4
|
0.5
|
0.6
|
|
ПАФ, h=1
|
0.04
|
0.07
|
0.11
|
0.15
|
0.20
|
0.25
|
|
ПАФ, h=2
|
0.05
|
0.06
|
0.08
|
0.10
|
0.13
|
0.16
|
|
ПАФ, h=3
|
0.09
|
0.10
|
0.10
|
0.11
|
0.12
|
0.15
|
|
ПАФ, h=4
|
0.15
|
0.15
|
0.16
|
0.16
|
0.17
|
0.18
|
|
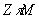
|
0.05
|
0.08
|
0.11
|
0.15
|
0.19
|
0.22
|
Из
полученных результатов можно заключить, что разработанный алгоритм ПАФ дает
значительное улучшение точности восстановления, которое во многом зависит от
правильного выбора размера окна 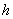 . Как видно из таблицы, наилучшие результаты оценки для
низкого уровня шума были получены при размере окна
. Как видно из таблицы, наилучшие результаты оценки для
низкого уровня шума были получены при размере окна 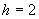 , а для высокого уровня шума при размере окна
, а для высокого уровня шума при размере окна 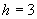 .
.
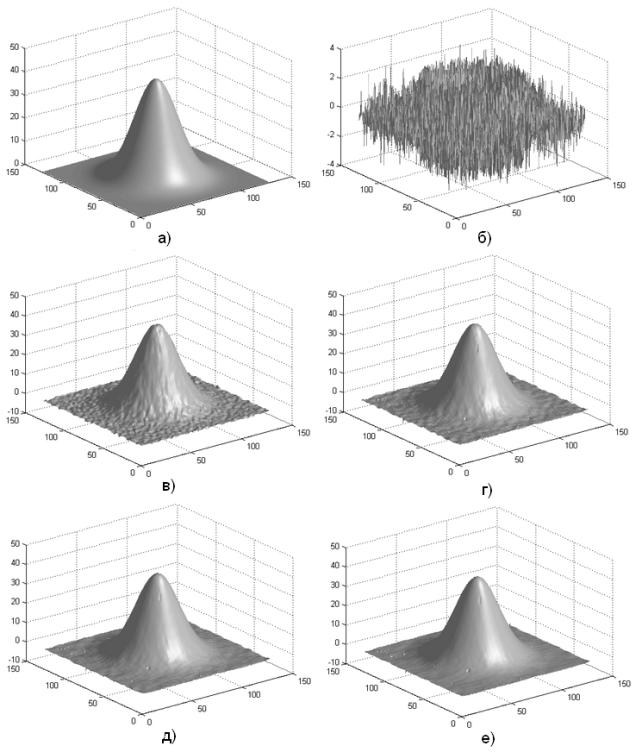
Рис. 3. a) Исходная
полная фаза 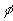 , б) наблюдаемая
свернутая фаза с Гауссовским белым шумом
, б) наблюдаемая
свернутая фаза с Гауссовским белым шумом  , в) восстановленная фаза
, в) восстановленная фаза  для значения размера
окна
для значения размера
окна  , г) восстановленная фаза
, г) восстановленная фаза 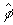 для значения размера
окна
для значения размера
окна 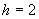 , д) восстановленная фаза
, д) восстановленная фаза 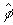 для значения размера
окна
для значения размера
окна 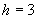 , е) восстановленная фаза
, е) восстановленная фаза 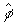 для значения размера
окна
для значения размера
окна 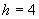 .
.
Литература:
1. Graham L. C. –
Synthetic interferometer radar for topographic mapping. In Proceedings of the
IEEE, 1974, v. 62, p. 763.
2. Goldstein R. M.,
Zebker H. A., Werner C. L. – Satellite radar interferometry: Two-dimensional
phase unwrapping. Radio Science, 1997, v. 23, p. 713.
3. Ghiglia D. C.,
Eichel P. H. – High-resolution synthetic aperture radar interferometry:
Technology for precise terrain elevation mapping. DSP and Multimedia
Technology, 1994, v. 3.
4. Arrasmith W. W.,
Roggemann M. C., Welsh B. M. – Optimal wave-front reconstruction for a coherent
diffracted field. Applied Optics, v. 37, No. 20, p. 4457, 1998.
5. Ghiglia D. C.,
Pritt M. D. – Two-Dimensional Phase Unwrapping: Theory, Algorithms, and
Software. New York: Willey, 1998.
6. K. Ho and J. Kahn,
“Exact probability density function for phase measurement interferometry,” J. Opt. Soc. Amer. A, vol. 12, pp. 1984–1989, 1995.
7. J. Lee, K. Hoppel,
S. Mango, and A. Miller, “Intensity and phase statistics of multilook
polarimetric and interferometric SAR imagery,” IEEE Trans. Geosci. Remote Sensing, vol. 32,
pp. 1017–1028, 1994.
8. S. Madsen,
“Spectral properties of homogeneous and nonhomogeneous radar images,” IEEE Trans. Aerosp. Electron. Syst., vol. AES-23, pp. 583–588, 1987.
9. C. Rathjen,
“Statistical properties of phase-shift algorithms,” J. Opt. Soc. Amer. A, vol. 12, pp. 1997–2008,
1995.
10. Katkovnik V., Egiazarian K., Astola J. – Local approximation techniques
in signal and image processing. SPIE PRESS, Bellingham, Washington, 2006.
11. J. Dias and J. Leitao, “The  algorithm: A method
for interferometric image reconstruction in SAR/SAS,” IEEE Trans. Image Process., vol. 11, no. 4, pp. 408–422,
Apr. 2002.
algorithm: A method
for interferometric image reconstruction in SAR/SAS,” IEEE Trans. Image Process., vol. 11, no. 4, pp. 408–422,
Apr. 2002.
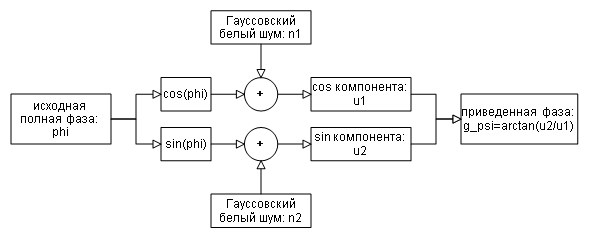
![]() и называется приведенной (интерферометрической) фазой.
Если значение полной фазы находится за пределами интервала
и называется приведенной (интерферометрической) фазой.
Если значение полной фазы находится за пределами интервала ![]() , то наблюдаемое значение будет свернуто в этот интервал
добавлением или вычетанием кратного
, то наблюдаемое значение будет свернуто в этот интервал
добавлением или вычетанием кратного ![]() числа. Таким образом
соотношение между приведенной фазой
числа. Таким образом
соотношение между приведенной фазой ![]() и полной фазой
и полной фазой ![]() задается следующим
образом
задается следующим
образом