Современные
информационные технологии/ 4. Информационная безопасность
к.т.н. В.Г.Ткаченко, к.ф.-м.н. О.В.Синявский
Одесская национальная академия связи им. А.С.Попова, Украина
КРИПТОСИСТЕМА НА ОСНОВЕ ОТОБРАЖЕНИЯ ТИПОВ МОНОТОННЫХ БУЛЕВЫХ ФУНКЦИЙ
(МБФ) НА МНОЖЕСТВО НАТУРАЛЬНЫХ ЧИСЕЛ.
В настоящее время передача цифровой
информации в телекоммуникационных системах получила широкое распространение. В
связи с этим возникает проблема повышения требований к обеспечению
информационной безопасности.
Наиболее часто в настоящий момент
используются асимметричные криптоалгоритмы или алгоритмы с открытым ключом. Но
алгоритмы с закрытым ключом гораздо проще реализуются как программно, так и
аппаратно и шифры с закрытым ключом работают быстрее шифров с открытым ключом.
Также надежность алгоритмов с открытым ключом в настоящее время обоснована
гораздо хуже, чем надежность алгоритмов с закрытым ключом. Поэтому для
организации шифрованной связи в настоящее время применяются шифры с закрытым
ключом, а новые методы применяются только там, где нельзя использовать
симметричные криптоалгоритмы, то есть для цифровой подписи или открытого
распределения ключей. В настоящее время блочные шифры являются основой, на
которой реализованы практически все криптосистемы (см. [1]-[5]). Все эти криптосистемы
не разработаны для блоков информации переменной длины, а используют блоки
постоянной длины. В [6] рассмотрено создание
криптосистемы с блоками переменной длины.
Однако в [6] передача ключей (типы
монотонных булевых функций) имеют сложную структуру, поэтому усложняется
передача ключа и снижается надёжность криптосистемы.
Назовем вектор Т = (a0, a1,…,ai,…,an)
из n + 1 компоненты, которые нумеруются слева направо от 0 до n,
типом МБФ, если i-я компонента вектора ai равна числу
подмножеств из i элементов в соответствующем данной МБФ семействе
подмножеств Шпернера. При этом одновременно i-я компонента вектора ai
равна числу минимальных входных наборов данной МБФ, лежащих на слое n – i булевого куба
ранга n.
Назовем число n рангом типа Т, число v ненулевых компонент
назовем весом типа Т, номер i первой
слева ненулевой компоненты назовем левой границей типа Т, номер j первой справа ненулевой компоненты правой
границей типа Т, сумму m всех компонент типа Т назовём мощностью типа. Тип Т называется максимальным, если при
увеличении любой его компоненты на 1, полученный вектор не будет являться
типом.
Будем считать, что тип МБФ Т1
больше типа Т2 МБФ если каждая компонента типа Т1 не
меньше соответствующей компоненты типа Т2.
Построим графическое представление этого
множества. Точкам будут соответствовать типы МБФ. Два типа будут соединены
тогда и только тогда, когда тип 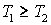 . Далее, каждому типу МБФ поставим в соответствие число, в
каноническом разложении которого степени простых будут соответствовать
компонентам типа. Например, типу ранга 5
. Далее, каждому типу МБФ поставим в соответствие число, в
каноническом разложении которого степени простых будут соответствовать
компонентам типа. Например, типу ранга 5 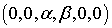 соответствует число
соответствует число 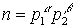 .
.
ПРИМЕР. Построим такое представление для
типов МБФ ранга 5 с таким набором простых чисел: 11, 5, 2, 3, 7, 13. Располагаем
простые по порядку их номеров в натуральном ряду и начинаем от центральной
компоненты типа. Вершины пронумеруем.

Рис. 1. Структура типов МБФ ранга 5.
Каждой вершины соответствует натуральное число и такой
тип МБФ:
Такая структура является полурешёткой
некоторой дистрибутивной решётки.
Получены следующие результаты.
Лемма
1. Структура типов МБФ изоморфна
полурешётки натуральных чисел, упорядоченных по делимости.
Лемма
2. Всё множество натуральных чисел
разбивается на бесконечное множество непересекающихся конечных классов, в
каждом их которых находятся числа с одинаковым рангом. При этом в каждом классе
содержится одно простое.
Построение
криптосистемы. Для построения
зашифрованного текста будем пользоваться двумя последовательностями ключей
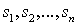
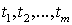
Для построения последовательностей S и T
будем использовать числа, находящиеся в узлах дерева типа МБФ (см. рис. 1). Для
сокрытия периодичности ключа можно использовать при построении
последовательностей S и T разные ранги типов МБФ. В работе [7]
показано, что количество типов растёт экспоненциально с увеличением ранга. Это
даёт возможность построения ключа равного по длине сообщения, что делает его
достаточно криптостойким.
С помощью первой последовательности мы
заменяем символы шифруемого текста на другие символы из того же алфавита,
который используется в исходном тексте, но под другим номером. Номер этого
символа определяем из соотношения
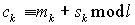 ,
,
где 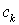 – символ шифротекста,
– символ шифротекста,
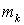 – символ открытого
текста,
– символ открытого
текста, 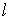 – длина алфавита.
– длина алфавита.
С помощью второй последовательности мы
переставляем биты уже полученного шифротекста. Номер переставляемого бита 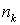 определяем по формуле
определяем по формуле
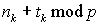 , где p – длина
сообщения в битах.
, где p – длина
сообщения в битах.
Итак, схема построения шифротекста должна
происходит в два этапа. Первый этап состоит в замене символов исходного текста,
использующего некоторый алфавит, другими символами того же алфавита. На втором
этапе происходит перестановка битов полученного промежуточного текста.
Дешифрование будем проводить в обратном
порядке.
Передачу ключа будем осуществлять с
помощью криптосистемы с открытым ключом. Например, для построения
последовательности чисел ранга 5, которая рассмотрена выше (см. пример), можно
передать только число 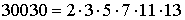 , т.е. для передачи нескольких последовательностей ключей
достаточно передать несколько таких чисел, а процедура расшифровки должна
находиться на стороне получателя шифрованного сообщения.
, т.е. для передачи нескольких последовательностей ключей
достаточно передать несколько таких чисел, а процедура расшифровки должна
находиться на стороне получателя шифрованного сообщения.
Литература
1.
Гатчин Ю.А. Основы криптографических
алгоритмов. Учебное пособие / Ю. А. Гатчин, А.Г. Коробейников– СПб: СПб
ГИТМО (ТУ), 2002. – 29 с.
2.
Чмора А.Л. Современная прикладная
криптография. 2-е изд. / А.Л. Чмора– М.:Гелиос АРВ, 2002. – 256 с. ил.
3.
Иванов М.А. Криптографические методы
защиты информации в компьютерных системах и сетях / М.А. Иванов– М.:
КУДИЦ-ОБРАЗ, 2001. – 368 с.
4.
Коробейников А.Г. Математические основы
криптографии. Учебное пособие / А. Г.
Коробейников–СПб: СПб ГИТМО (ТУ), 2002. – 41 с.
5.
Аграновский А.В. Классические шифры и
методы их криптоанализа / А.В. Аграновский, А.В Балакин, Р.А. Хади // М: Машиностроение: Информационные
технологии, 2001 – № 10 – С. 40 – 45.
6.
Ткаченко В.Г. Деревья типов монотонных
булевых функций и криптосистемы с блоками переменной длины /
В.Г. Ткаченко, О.В.Синявский // Наукові праці ОНАЗ ім. О.С. Попова. –
Одеса, 2009. – №2. – С. 32 – 42.
7.
Ткаченко В.Г. Перечисления типов монотонных
булевых функций при синтезе цифровых схем / В.Г. Ткаченко // Наукові праці
ОНАЗ ім. О.С. Попова. – Одеса, 2008. – №2. – С. 54 – 69.
![]() . Далее, каждому типу МБФ поставим в соответствие число, в
каноническом разложении которого степени простых будут соответствовать
компонентам типа. Например, типу ранга 5
. Далее, каждому типу МБФ поставим в соответствие число, в
каноническом разложении которого степени простых будут соответствовать
компонентам типа. Например, типу ранга 5 ![]() соответствует число
соответствует число ![]() .
. 