М.П. Ленюк, О.М. Ленюк

Чернівецький національний університет імені Юрія Федьковича

Запровадження гібридного інтегрального перетворення типу

Бесселя – Ейлера – Лежандра на полярні вісі

 

Нехай – диференціальний оператор Бесселя [1];  – диференціальний оператор Ейлера [2];–узагальнений диференціальний оператор Лежандра [3];  .

Розглянемо гібридний диференціальний оператор (ГДО)

        (1)

Означення: За область визначення ГДО  приймемо множину  G вектор-функцій  з такими властивостями: 1) вектор-функція  неперервна на множині

2) функції  задовольняють крайові умови

                                 (2)

3) функції  задовольняють умови спряження

                   (3)

Вважаємо, що виконані умови на коефіцієнти: ,  .

Оператор  як сполучення самоспряжених операторів є самоспряженим оператором і має одну особливу точку . Тому його спектр дійсний та неперервний [4]. Можна вважати, що спектральний параметр . Йому відповідає спектральна вектор-функція

.

Функції  задовольняють крайові умови (2), умови спряження (3) та диференціальні рівняння

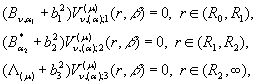                                 (4)

Фундаментальну систему розв’язків для диференціального рівняння Бесселя  утворюють функції  та  [1]; фундаментальну систему розв’язків для диференціального рівняння Ейлера  утворюють функції  та  [2]; фундаментальну систему розв’язків для диференціального рівняння Лежандра  утворюють функції  та ,  [3].

Покладемо

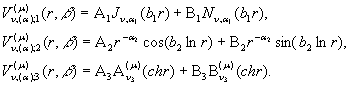                                        (5)

Крайові умови (2) та умови спряження (3) для визначення величин  дають алгебраїчну систему з п’яти рівнянь:

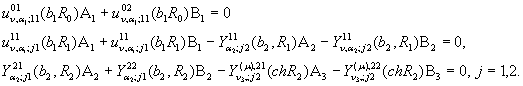(6)

У системі (6) беруть участь загальноприйняті функції [4].

Візьмемо де  підлягає вибору. Перше рівняння в системі (6) стає тотожністю, а інші рівняння утворюють дві алгебраїчні системи по два рівняння в кожній.

Розглянемо першу алгебраїчну систему:

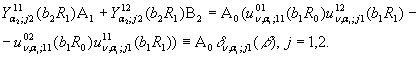                (7)

Визначник алгебраїчної системи (7)

За правилами Крамера [5] отримуємо:

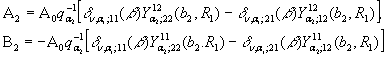                                           (8)

Розглянемо другу алгебраїчну систему:

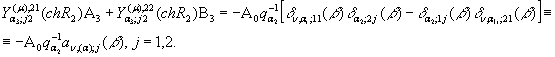            (9)

Визначник алгебраїчної системи (9)

Тут бере участь функція

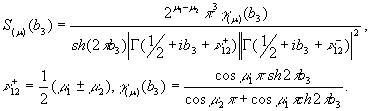
Згідно правил Крамера [5] маємо при , що

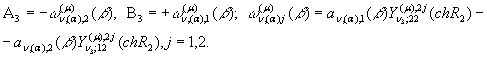          (10)

Підставивши в рівності (5) визначені згідно рівностей (9), (10) величини , одержуємо функції:

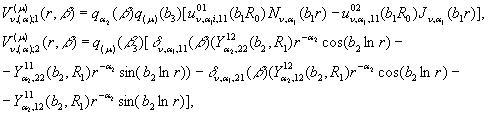           (11)

Визначимо вагову функцію

 та спектральну щільність

.

Тут беруть участь величини:

, , s3 = .

 

Наявність спектральної функції , вагової функції  та спектральної щільності  дозволяє запровадити гібридне інтегральне перетворення, породжене на множині  ГДО M:

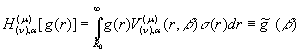                                     ,                              (12)

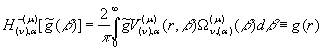                                  .                            (13)

Математичним обґрунтуванням формул (12), (13) є твердження.

Теорема 1 (про інтегральне зображення). Якщо вектор-функція

 неперервна абсолютно сумовна й має обмежену варіацію на множині , то для будь’якого   має місце інтегральне зображення

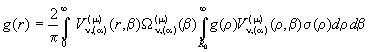                                                   (14)

Доведення. В основі доведення лежить невласний інтеграл

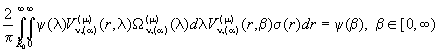                    (15)

Функція  неперервна, абсолютно сумовна з обмеженою варіацією на множині .

Припустимо, що функція

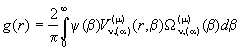                                  (16)

Помножимо рівність (16) на вираз , де  – довільне додатне число, й проінтегруємо від  до . Внаслідок рівності (15) одержуємо:

.

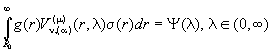Підставивши в рівність (16) функцію 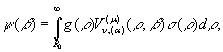 одержуємо інтегральне зображення (14)

Зауваження: Якщо вектор-функція  кусково-неперервна, то зліва в (14) треба замість  писати

Застосування запровадженого формулами (12), (13) гібридного інтегрального перетворення до розв’язування відповідних задач математичної фізики неоднорідних середовищ базується на основній тотожності інтегрального перетворення ГДО , визначеного рівністю (1).

Теорема 2 (про основну тотожність). Якщо вектор-функція f(r) = {; }  неперервна на множині , а функції задовольняють крайові умови

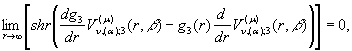           (17)

та умови спряження

                               (18)

то справджується основна тотожність інтегрального перетворення ГДО , визначеного рівністю (1):

-+

+                                                                                         (19)

У рівності (19) прийняті позначення:

  ,    

 ;   ,  ,

        

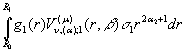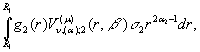
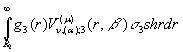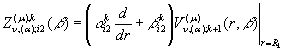, i,k = 1, 2.

Доведення. Згідно формули (12)

+

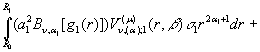
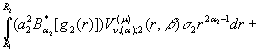
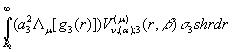
Проінтегруємо під знаком інтегралів два рази частинами:

 

  

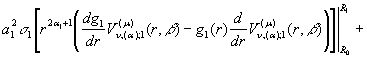
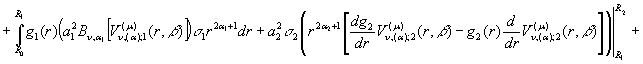
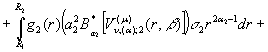
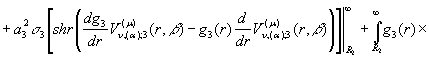
                                                                     (20)

В силу диференціальних рівнянь, які задовольняють функції , знаходимо тотожності:

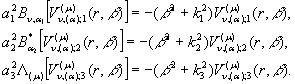                                                        (21)

При  маємо:

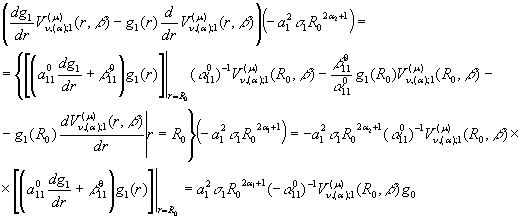   (22)    

В силу граничної рівності (17) позаінтегральний доданок при  обертається в ноль.

На підставі базової тотожності

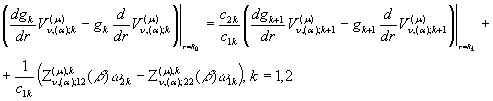
при маємо послідовно:

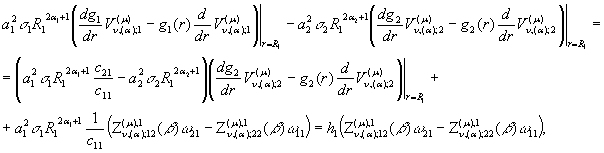 (23)

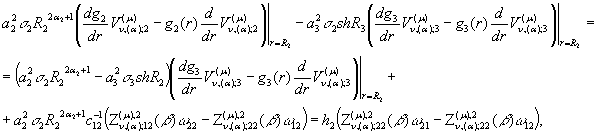(24)

Ми прийняли до уваги, що в силу вибору , та