Мельник В.Н., Карачун В.В.

Национальный технический университет Украины «КПИ»

УРАВНЕНИЯ ПОДВЕСА ГИРОСКОПА ОБОЛОЧЕЧНОЙ ФОРМЫ ПРОИЗВОЛЬНОГО ОЧЕРТАНИЯ

Решение задачи взвешивания гироузла, т.е. перехода к многофазному подвесу, позволило значительно повысить вибро- и удароустойчивость приборов, снизить сухое трение на выходной оси и, естественно, порог чувствительности. Кроме того, значительно улучшились демпфирующие свойства за счет увеличения вязкого сопротивления.

Вибрация входит внутрь прибора через опоры. Поэтому такое решение было оправдано для определенных Технических условий. Вместе с тем, пространственное нагружение – акустическое излучение, тепловой факел и т.п. – попадающие внутрь не только через опоры, но и через среду, имея на пути распространения волны возмущения жидкофазную структуру, получили облегченный доступ внутрь, со всеми вытекающими последствиями.

Таким образом, возникает задача максимального сохранения первоначальной идеи, как убедительно доказавшей свою состоятельность, наряду с изменением геометрии поплавка подвеса переходом от классического цилиндра к оболочке вращения с произвольной геометрией очертания линии меридиана.

Сохраняя за классическим цилиндром несомненные достоинства как наиболее простого с точки зрения технологии изготовления, следует отметить его недостаточную жесткость в плоскости шпангоута при значительных ее величинах вдоль параллели и протяженности. При силовом нагружении (например, акустическом, в 150 - 160 дБ) это неизбежно приводит к упругим деформациям поверхности подвеса, которые в своей совокупности воспринимаются гироскопом как «ложный» входной сигнал [1].

Произвольное очертание оболочечной части подвеса позволит не только четче сформулировать методику анализа, но создаст научную базу для сравнительного изучения явления [2, 3]. Как частное, строится картина прохождения звука через цилиндр [4].

Построим математическую модель упругого взаимодействия проникающего волнового воздействия, например, акустического, с поверхностью поплавка с произвольным очертанием линии меридиана.

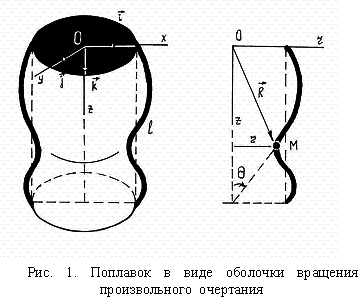
Оболочка вращения произвольной формы образуется при вращении любой кривой вокруг выбранной оси симметрии оболочки. Предполагаем, что эта кривая не пересекает ось вращения (рис.1). Опорная (инерциальная) и связанная системы координат изображены на схеме. Здесь приняты следующие обозначения: r = f(z)- кривая вращения; r –расстояние от оси вращения до рассматриваемой точки М.

Примем длину оболочки равной l. Тогда z[0,l].

Пусть φ - координата, определяющая положение т. М на параллели. Тогда, для бесконечно малого расстояния между двумя точками по срединной поверхности π оболочки, можно записать соотношение:

где dS₁ – дифференциал дуги по меридиану; dS₂ – дифференциал дуги вдоль параллели.

Так как

то – (1)

Отсюда следует, что в качестве координат α₁ и α₂целесообразно выбрать следующие:

.

Тогда

(2)

Это дает возможность сделать важный вывод: параметры Ламе А₁ и А₂ являются функциями одной координаты – z.

В качестве координат можно выбрать и другие криволинейные координаты, например, (здесь - угол между нормалью к поверхности π и осью вращения оболочки (рис.1)).

Запишем уравнения движения оболочки в координатах В этом случае в исходных уравнениях следует произвести соответствующие замены в обозначениях [5]:

С учетом сказанного, эти уравнения примут иной вид. Первое уравнение, по координате , запишется в форме –

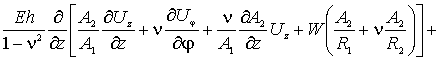
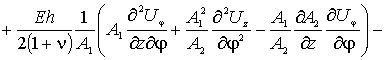
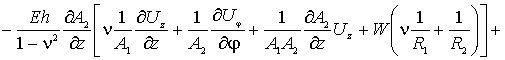
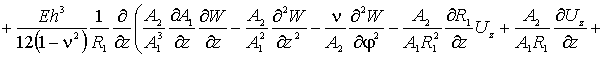
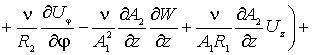(3)

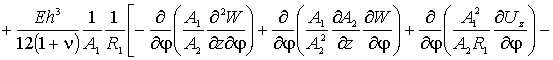
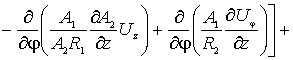
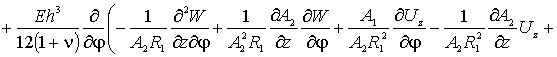
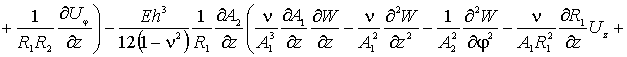
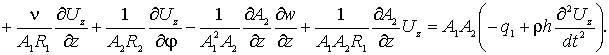По координате уравнение имеет вид -

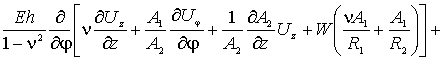
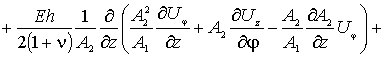
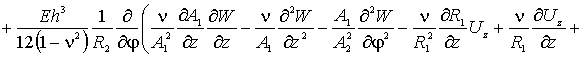
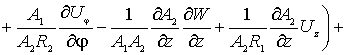
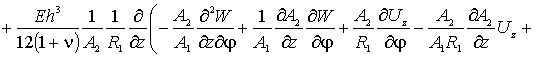(4)

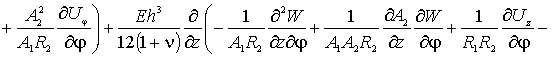
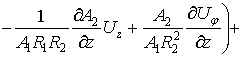
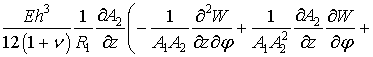
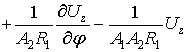
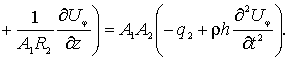
Наконец, по координате (прогибы оболочки), уравнение запишется так

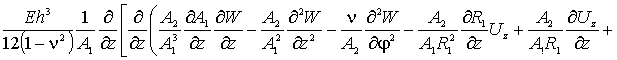
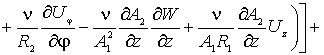
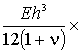
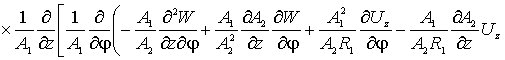
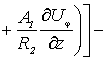
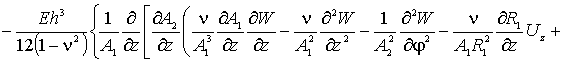
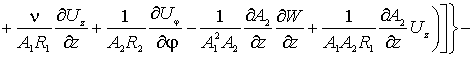
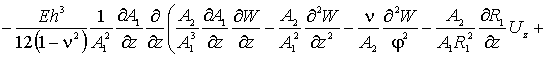
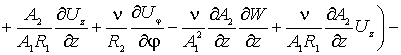
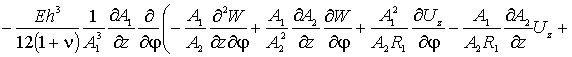
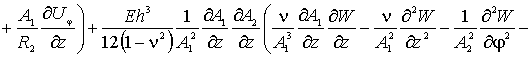
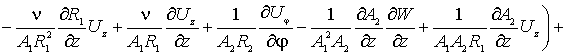
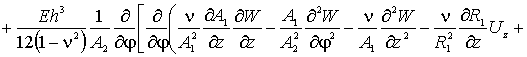
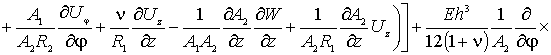(5)

,

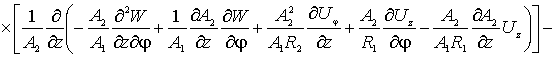
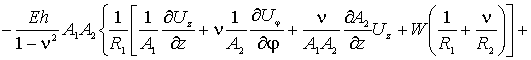
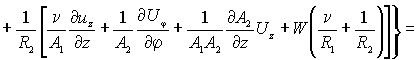
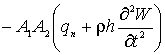где - упругие перемещения поверхности оболочки вдоль ее протяженности, вдоль параллели и в направлении радиуса соответственно; А₁ , А₂ – параметры Ламе срединной поверхности; - коэффициент Пуассона; Е – модуль Юнга; h – толщина оболочки; R₁ , R₂ – радиусы кривизны линии координатных функций и ; q₁, q₂ , q₃ – внешние возмущения.

Как частный случай, из (3-5) получаются уравнения круговой цилиндрической оболочки. Для этого достаточно принять следующие значения постоянных Ламе: А₁=1; А₂=R=const.

Правая часть уравнений подвеса представлена в общем виде, что дает возможность решать множество практических задач. Левая часть уравнений позволяет определить partialis частоты поплавка, а также установить степень перекрестного влияния двух других координатных функций.

Наконец, не представляет труда составить уравнение частот, очертить границы степени проявления всех трех (или каждой в отдельности) координат. С этой целью, для различного класса задач необходимо корректно сформулировать граничные условия.

Таким образом, получены дифференциальные уравнения подвижной части поплавкового гироскопа, позволяющие решать задачи анализа упругого взаимодействия поплавка с внешними воздействиями, с одной стороны, решать задачи синтеза с целью уменьшения погрешностей приборов такой технической реализации – с другой.

Представляет научный и практический интерес продолжение исследований на предмет возникновения особенностей в подвесе. Изучить влияние геометрии линии меридиана, а также структурной нелинейности, на резонансные проявления в импедансных конструкциях, особенно при антисимметричном нагружении.

ЛИТЕРАТУРА:

1. Карачун В.В., Лозовик В.Г., Мельник В.Н. Дифракция звуковых волн на подвесе гироскопа. . - К.: ²Корнейчук², 2007. - 228 с.

2. Мельник В.Н., Карачун В.В. Некоторые аспекты гироскопической стабилизации в акустических полях // Прикл. механика. 2002, №1. - С.95 - 101.

3. Mel¢nick V.N., Karachun V.V. Influence of acoustic radiation on the sensors of a gyrostabilization platform // International Applied Mechanics/ - Vol.40. - №10, 2004. - P.122 – 130.

4. Мельник В.Н., Карачун В.В. Інжекція акустичної енергії РН і її вплив на похибки гіроскопа // Вісник ЖДТУ. - 2004. - Т.1. - №4(31). /Технічні науки. - С.135 – 138.

5. Карачун В.В., Каюк Я.Ф., Мельник В.Н. Волновые задачи поплавкового гироскопа. - К.: ²Корнейчук², 2007. - 228 с.