УДК 339.144

Казангапова Баян Алькеновна, к.т.н., доцент

Али Жулдыз, Абдиуалиева Асель, Терликпаева Айгул 4-курс студенты

АЛМАТИНСКИЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ

РАЗРАБОТКА МОДЕЛЕЙ УПРАВЛЕНИЯ ЗАПАСАМИ

В условиях перехода РК к рыночным отношениям проблема усовершенствования структуры и методов управления предприятием становится одной из наиболее важных, так как от качества управления, оптимизации его структуры зависит выживание субъекта хозяйствования в конкурентной борьбе. В силу этого теоретическое исследование управления запасами промышленного предприятия и обоснованный выбор математической модели и метода для его решения является актуальным.

Для решения проблем, связанных с запасами предназначены модели управления запасами. Модели должны отвечать на два основных вопроса: сколько заказывать продукции и когда.[1] Есть множество разнообразных моделей, каждая из которых подходит к определенному случаю.

Все модели управления запасами можно разделить на группы:

· детерминированы модели управления запасами.

· модели оперативного управления запасами при случайном спросе

· модели управления запасами в системе с периодическими проверками при случайном спросе.

· модели управления запасами в течение одного периода.

· динамические модели управления запасами.[2]

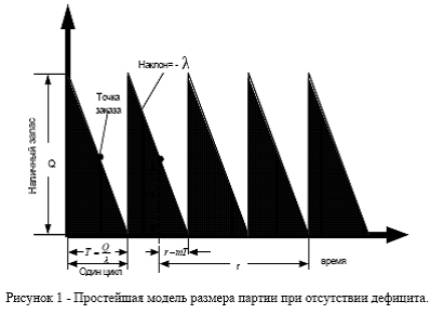
Рассмотрена простейшая модель размера партии при отсутствии дефицита на одиночной базе при условии, что спрос детерминирован, и интенсивность поступления требований равна λ единиц в год вне зависимости от времени. Предполагаем, что время поставки τ постоянно и не зависит от λ и размера заказа. Заказ поступает в виде одной партии. Будем считать, что товар может храниться неограниченное время и что он не устаревает. Тогда удобно считать, что система будет продолжать работать и в будущем. Очевидно, что если данная система функционирует оптимально, то при подаче заказа каждый раз заказывается одно и то же количество товара, а уровень наличного запаса в момент поступления пополнения всегда один и тот же. Минимизация издержек обеспечит отыскание той же самой стратегии функционирования, что и максимизация прибыли. Оптимальная стратегия функционирования будет определяться из условия минимума средних годовых издержек.

Оптимальное значение Q определяется по формуле Уилсона

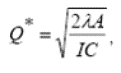
где А - стоимость подачи заказа;

С - стоимость единицы товара при подаче заказов на партии из Q единиц ;

I - коэффициент издержек.

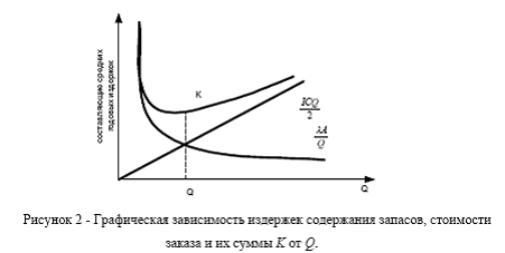
На практике на большинстве складов хранится большое число различных типов изделий. Взаимодействие между изделиями может носить различный характер. Например, изделия могут частично заменять друг друга, изделия могут конкурировать при ограничении на площадь склада. Может существовать верхний предел общего числа заказов, и потому изделия могут вступать в конкуренцию из-за этого фактора. Рассмотрим случай, когда в каждый момент времени существует верхний предел D капиталовложений. Ограничение имеет вид

Пусть λj означает годовую интенсивность спроса (предполагается, что спрос не случаен), Aj – фиксированные издержки заказа, Сj - стоимость единицы изделия (предполагается, что она не зависит от Qj) и Ij- коэффициент издержек содержания изделий j-го типа. Тогда суммарные годовые издержки по всем типам изделий составят

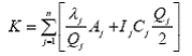
Нужно минимизировать выражение (3) при наличии ограничения (2). Сначала решается задача пренебрегая ограничением (2). Если полученное решение удовлетворяет (2), то задача решена. Если (2) не удовлетворяется, то вводятся множители Лагранжа θ, φ [3] и составляется функция

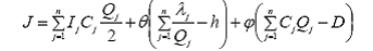
Тогда оптимальные значения Qj должны быть решениями уравнений

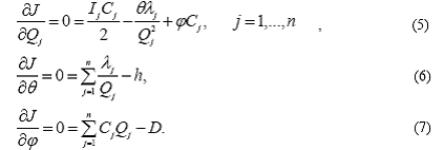
Из (5) следует, что оптимальное значение Qj*

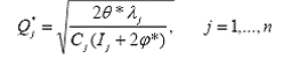
Тогда, подставляя Qj* из (8) в (6) получим

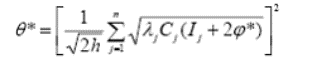
Последовательно подставляя θ* из (9) в (8) и Qj* из (8) в (7) получим

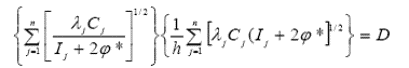
Процедура численного решения состоит в следующем:

1) Определяем φ* из (10)

2) Определяем θ* из (9)

3) Определяем Qj* из (8) [4]

Значение φ* можно определить из (10) методом проб и ошибок. Однако более эффективным оказывается метод Ньютона.

Рассмотрим уравнение f(x)=0. Предположим, что x0 является приближенным решением, т.е. значение f(x0) близко к 0. Используя первые два члена разложения в ряд Тейлора, имеем

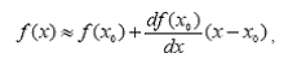
где x близко к x0. Полагая f(x)=0, имеем

Заметим, что в качестве новой оценки решения уравнения f(x)=0 можно использовать x1=x0+Δx. Такой процесс повторяется, и на (n+1)-м шаге имеем

Описанная процедура отыскания решения уравнения f(x)=0 и называется методом Ньютона [2]

Правильное и своевременное определение оптимальной стратегии управления запасами, а также нормативного уровня запасов позволяет высвободить значительные оборотные средства, замороженные в виде запасов, что в конечном счете повышает эффективность используемых ресурсов.[1]

Список литературы

1. Кремер Н.Ш. Исследование операций в экономике, М.:Юнити, 2002.- 407 c.

2. Хедли Дж., Уайтин Т. Анализ систем управления запасами, перев. с англ., М.:«Наука», 1969. - 511 c.