Доктор физ.-мат. наук А.В.
Макаричев, А. А. Кудь, А.Б.Щукин
Московский государственный университет им. М.В. Ломоносова
Харьковский национальный автомобильно-дорожный университет
Национальный аэрокосмический
университет «ХАИ»
ИНВАРИАНТНАЯ ДИСЦИПЛИНА В МНОГОЛИНЕЙНОЙ СИСТЕМЕ МАССОВОГО
ОБСЛУЖИВАНИЯ С ОГРАНИЧЕННЫМ ЧИСЛОМ ПРИБОРОВ ОБСЛУЖИВАНИЯ БЕЗ ОЖИДАНИЯ
Рассмотрим
многоканальную систему массового обслуживания, состоящую из ![]() обслуживающих
приборов с входящим пуассоновским простейшим потоком требований с параметром
обслуживающих
приборов с входящим пуассоновским простейшим потоком требований с параметром ![]() и функцией
распределения длины требования
и функцией
распределения длины требования ![]() . Приведем описание дисциплины обслуживания в этой системе.
Если в системе массового обслуживания есть один или несколько свободных
приборов, поступающее требование занимает свободный обслуживающий прибор и
обслуживается на нем со скоростью единица. Если же в системе число требований
больше, чем число приборов, то все требования в системе обслуживаются с одинаковой
скоростью так, что сумма их скоростей обслуживания равна
. Приведем описание дисциплины обслуживания в этой системе.
Если в системе массового обслуживания есть один или несколько свободных
приборов, поступающее требование занимает свободный обслуживающий прибор и
обслуживается на нем со скоростью единица. Если же в системе число требований
больше, чем число приборов, то все требования в системе обслуживаются с одинаковой
скоростью так, что сумма их скоростей обслуживания равна ![]() .
.
Обозначим ![]()
математическое ожидание длины требования,
![]()
нагрузку на систему массового обслуживания. Обозначим через
![]() общее число
требований в системе массового обслуживания. Оставшуюся длину дообслуживания
общее число
требований в системе массового обслуживания. Оставшуюся длину дообслуживания ![]() го требования
(нумерация идет от единицы в порядке поступления – меньший номер у ранее
пришедшего требования) обозначим через
го требования
(нумерация идет от единицы в порядке поступления – меньший номер у ранее
пришедшего требования) обозначим через![]() . Случайный процесс
. Случайный процесс
![]()
показывает состояние процесса обслуживания в
многоканальной системе в момент времени ![]() . Обозначим
. Обозначим ![]() ,
,
![]() ,
, ![]() .
.
Вероятности ![]() того, что в системе
массового обслуживания в момент
того, что в системе
массового обслуживания в момент ![]() находятся ровно
находятся ровно ![]() требований,
определяются по формулам:
требований,
определяются по формулам:
![]() при
при ![]() ,
,
![]() при
при ![]() ,
,
а соответствующие стационарные вероятности существуют
когда ![]() [1] и равны
[1] и равны ![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
Следуя
нашим великим учителям [1-5], составим систему дифференциальных уравнений
Колмогорова для стационарных вероятностей состояний случайного процесса: ![]() , когда
, когда ![]() ,
,
![]() , при
, при ![]()
![]()
![]()
![]() при
при ![]() .
.
Составим
так же уравнения Колмогорова в частных производных для стационарных
вероятностей состояний случайного процесса
![]()
![]()
![]() и для
и для ![]() .
.
Группируя равные нулю суммы слагаемых в уравнениях,
представим решение данной бесконечной системы дифференциальных уравнений в
частных производных для стационарных вероятностей состояний случайного процесса
в виде
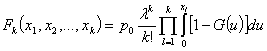 , при
, при ![]()
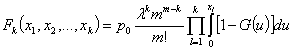 , при
, при ![]() , где
, где
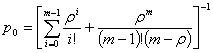 ,
,
в чем можно
убедиться, непосредственно подставляя его в дифференциальные уравнения. Отсюда
при ![]()
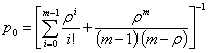
![]() при
при ![]() и
и
![]() при
при ![]() .
.
Заметим,
что при таком характере обслуживания требований в многоканальной системе
стационарные вероятности состояний случайного процесса числа требований в
системе при фиксированном математическом ожидании времени обслуживания
требований не зависят от вида его функции распределения.
Предположим,
что входящий поток требований является результатом наложения простейших потоков
с интенсивностями ![]() ,
,
![]() ,
,
от ![]() источников. Обозначим
через
источников. Обозначим
через ![]() ,
, ![]() . Тогда стационарные
вероятности
. Тогда стационарные
вероятности ![]() того, что в системе обслуживания находятся ровно
того, что в системе обслуживания находятся ровно ![]() требований и среди
них ровно
требований и среди
них ровно ![]() требований из
требований из ![]() -го источника,
-го источника, ![]() , определяются по формулам
, определяются по формулам
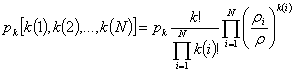 ,
, ![]() .
.
Используя выражения для стационарных вероятностей ![]() , когда
, когда ![]() , получим
, получим
![]()
для ![]() и
и
![]()
для натуральных чисел ![]() , где
, где
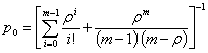 .
.
Литература
1. B. V. GNEDENKO AND
I. N. KOVALENKO, Introduction to Queueing
Theory, Program for Scientific Translations, Jerusalem, 1968.
2.
Вопросы математической теории надежности /Е.Ю.
Барзилович, Ю.К. Беляев, В.А. Каштанов, И.Н. Коваленко,
А.Д. Соловьев, И.А. Ушаков; Под ред. Б. В. Гнеденко.- М.:
Радио и связь, 1983.- 376 с., ил.
3.
Б.А. Севастьянов.
Эргодическая теорема для Марковских
процессов и ее приложения к телефонным системам с
отказами. Теория вероятностей и ее применения, т. 2, вып. 1,
1957, 106-116.
4. А.Н. Ширяев. Вероятность, М.: Наука,
1980, 576 c.
5. R. Fortet. Theorie
des probabilities, Centre Nat. Rech. Scient.,
Paris, 1950.