Е.Т.Божанов,
К.Д.Мурзасаимова, М.Т.Касымбекова
Казахский
национальный исследовательский технический университет имени К.И.Сатпаева,
Казахстан,
Алматы
УДК 532:536.24;533.9
Рассмотрим порошковую формовку
конструкционного порошкового материала, которая в процессе прессования дополнительно
засыпается порошком через вертикальный канал матрицы пресс-штемпеля путем
пульсации под давлением ударного импульса. Зона максимальной плотности
находится от прессующего пуансона на
расстоянии L. Масса слои порошка до
засыпания m0, то после засыпания
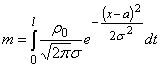, где 
.
а-
математическое ожидание, 
дисперсия.
Уплотнение порошкового материала
рассмотрим в зависимости от модуля упрочнения – 
,
где
- остаточная деформация, 
- напряжение, 
- температура, 
- время, 
- пластическая деформация при нагружении, 
- параметры структурного изменения порошка.
Считая, что слои порошка, есть эквивалентный
слой на торцах поверхности примем следующие граничные условия:
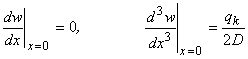(1)
(условие
под нагрузкой ударного импульса), где 
- внешняя активная критическая сила,
(2)
шарнирные закрепления эпитрохоидные и гипотроихоидные
схемы.
Тогда в процессе прессовки в качестве математической
модели упрочнения порошка будет [1]-[4].
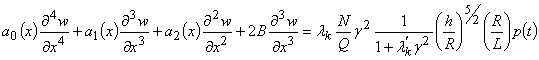(3)
, 
, 
с граничными
условиями (1)-(2).
Здесь 
- коэффициент формы поперечного сечения порошковой формовки; В- коэффициент континиуума Коссера, имеющий размерность силы, но намного меньше
модуля Юнга, 
, 
- формы нелинейных
деформационных процессов, 
- анизотропные характеристики.
Здесь:
- модуль упругости, 
- плотность эквивалентного слоя, 
- коэффициенты взаимного влияния из допущения о существовании
упругого потенциала, 
- плотность слои порошка, 
- температура, 
- удельная теплоемкость, 
- коэффициент теплопроводности, 
- фазовая скорость, 
- дисперсионные соотношения для фазовой скорости, 
- модуль сдвига эквивалентного слоя.
Решение систем дифференциального
уравнения (3) следует искать методом разделения переменных с учетом
распространения тепла в стержнях за пределом теории упругости:
(4)
где
- температура, 
- площадь поперечного сечения, 
- удельная теплоемкость стержня на единицу длины, 
- коэффициент теплопроводности, 
- плотность, которая определяется по формулам:
, 
, 
, 
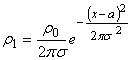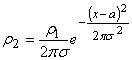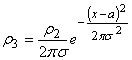(5)
- плотность тепловых источников, 
- коэффициент теплообмена с внешней средой, 
- диаметр стержня, 
- температура внешней среды.
Тогда с учетом только лишь
внутренних критических сил в предположении, что комплексная податливость
материала распространения тепла, а так же изменение времени по модели из одного
стержня и двух демперов
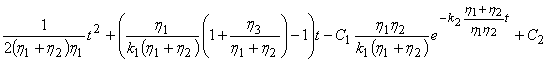(6)
влияет
лишь на анизотропные характеристики 
, но не влияет на коэффициент потерь
(7)
где
- амплитуда напряжения внутреннего трения, 
- амплитуда упругого напряжения, в качестве математической
модели предлагаем:
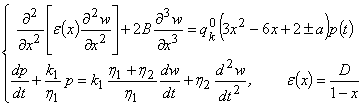(8)
Общее
решение собственного возмущения есть:
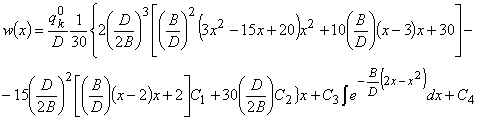(9)
где 
определяется с учетом
формулы (4).
В частности, если дифференциальное
уравнение изгибающего момента центральной оси поперечного сечения возьмем с
учетом геометрической нелинейностей в виде:
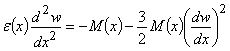(10)
С
учетом геометрической и физической нелинейностей
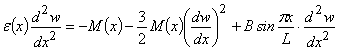(11)
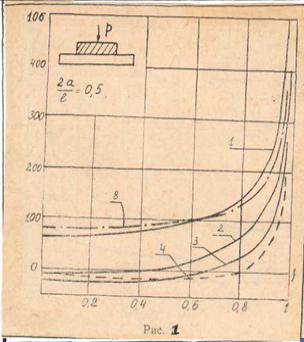
Упругих
решении А.Ю.Ильюшина, то давление передаваемое штампом совпадает с давлением,
производимым штампом на упругую полуплоскость, в случае одностороннего контакта
и является положительным (Рис. 1).
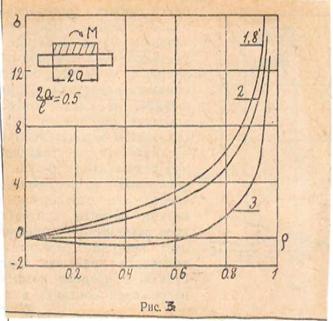
В случае двухстороннего контакта для
тонких трубчатых конструкции давление становится отрицательным (Рис. 2).
Вблизи края решение контакта,
необходимо найти частное решение дифференциального уравнения
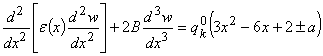(12)
при
заданных граничных условиях и условиях под нагрузкой (1)-(2)
из общего решения (9).
|
|
|
|
|
|
|
|
|
|
Выводы:
1.
Внутреннее нагружение поперечного сечения листовой
заготовки критическим импульсом повышает коэффициент динамичности МП.
2.
Образование «брикета» и прессуемость МП (металлического
порошка) зависят от нелинейных деформационных процессов начального объема
пресс-формы.
3.
Длина листовой заготовки почти не влияет на величину
критического импульса, который существенным образом зависит от вида функции 
. Благодаря неглубокой активности ударного импульса
поверхностное напряжение уменьшается в сторону основания торцевого сечения и
поперечного сечения, теряет устойчивость. Пресс-форма имеет довольно сложную
конфигурацию.
4.
Локальная импульсивная нагрузка возбуждает в пресс-форме
волновой процесс, который существенным образом завасит от степени комплексной
податливости порошка и амплитуды силы внутреннего трения. Происходит изгибание
у опоры пресс-формы и у наполнителя в поперечном сечении, имеющий местный
характер.
5.
Предложенная модель в задачах технологии новых материалов
имеет место в технологии прессования и спекания порошкового материала, а также
в задачах контактного воздействия.
Литература.
1.
Божанов
Е.Т., Ержанов Ж.С. Исследование проблем устойчивости упругих тел, гибких
пластин и оболочек и их приложения// Алматы:
Қазақстан жоғары мектебі.2001. 325с.
2.
Цейтлин А.И., Кусаинов А.А. Методы учета внутреннего
трения в динамических расчетах конструкций// Алма-Ата, 1987. 238с.
3.
Братухин А.Г., Сироткин О.С., Сабодаш П.Ф., Егоров В.Н.
Материалы будущего и их удивительные свойства// Москва: Машиностроение. 1995.
125с.
4.
Божанов
Е.Т., Отарбаев Ж.О., Буганова С.Н. Математическое моделирование геомеханических
процессов. Алматы, 2015. 145с.