УДК 22.1 Педагогика/ 1. Математика

Адеева Толкын Койшымановна

учитель математики, средняя школа №29 имени Ю. Гагарина, г. Тараз, Республика Казахстан

Повышение вычислительной культуры школьников

на уроках математики

Развитие общества требует постоянного улучшения качества обучения, трудового и нравственного воспитания учащихся. Поэтому, важнейшей задачей обучения математике является обеспечение прочного и сознательного овладения учащимися математическими знаниями и умениями, нужными в повседневной жизни и в работе каждого члена современного общества. В связи с этим необходимо подчеркнуть роль вычислительной подготовки учащихся в системе общего образования. Вычислительная культура является тем запасом знаний и умений, который находит повсеместное применение, является фундаментом изучения математики и других учебных дисциплин. Кроме того, вычисления активизируют память учащихся, их внимание, стремление к рациональной организации деятельности и прочие качества, оказывающие существенное влияние на развитие учащихся. Однако уровень навыков вычислений и тождественных преобразований у учащихся резко снизился: они плохо и нерационально считают, кроме того, при вычислениях все чаще прибегают к помощи технических средств – калькуляторов. Еще одна проблема современных учащихся, которая напрямую связана с вычислительной культурой, – нерациональность вычислений. Нужно обучать школьников не только выбирать и осуществлять рациональный путь выполнения упражнений и решения задачи, но и рационально записывать то или иное решение. Возникает потребность в ознакомлении учащихся с дополнительными приемами устных и письменных вычислений, которые позволили бы значительно сократить время, потраченное на вычисления и запись решения, и избежать использования различных вычислительных средств.

Одной из основных задач преподавания курса математики в школе является формирование у учащихся сознательных и прочных вычислительных навыков. Вычислительные навыки – важная составляющая математических навыков. Большая часть математических навыков – это сложные навыки, формирующиеся на основе других умений и навыков. Так, навык сложения дробей с разными знаменателями основан на умении находить наименьшее общее кратное двух натуральных чисел, применять основное свойство дроби при приведении дробей к общему знаменателю, складывать дроби с одинаковыми знаменателями. В свою очередь каждые из указанных умений и навыков также имеют сложную структуру. Отсутствие какого-либо из элементарных умений и навыков служит причиной несформированности сложного навыка. Общеизвестно, что умения и навыки быстрее усваиваются и дольше сохраняются, если их формирование происходит на сознательной основе (дидактический принцип сознательности). Тренировки без достаточного понимания изучаемого редко приводят к прочным умениям и навыкам. Поэтому формированию навыков учащихся должно предшествовать понимание ими сути изучаемого действия.(6)

Формирование математических навыков состоит из следующих этапов:

1. Первый этап формирования навыка – овладение умением.

2. Второй этап – этап автоматизации умения.(4)

Актуальным является методическое требование выполнять устно вычисления и преобразования не только во время так называемых пятиминуток устного счета. При решении любых задач, на каждом этапе урока все вычисления и выкладки, которые ученики могут выполнять устно, должны быть устно и выполнены. Привычка выполнять устно несложные вычисления и выкладки нередко порождает потребность производить мысленные эксперименты при решении задач, высказывать догадки, предположения о путях решения более сложных задач, мысленно (устно) проверяя истинность предположений. А это одно из главных условий обучения решению математических задач. Обдуманное составление плана существенно помогает выбору рационального пути решения. Рациональное же решение – способ развития мышления учащихся, формирования высокоразвитых, осмысленных умений и навыков, свидетельствующий о бережном отношении учителя к учебному времени учащихся. Задача учителя систематически обращать внимание школьников на рационализацию вычислений и преобразований. Таким образом, подчеркнув особенности математических навыков, можно переходить к рассмотрению частного случая – вычислительным навыкам.(2)

О наличии у учащихся вычислительной культуры можно судить по их умению производить устные и письменные вычисления, рационально организовывать ход вычислений, убеждаться в правильности полученных результатов. Качество вычислительных умений определяется знанием правил и алгоритмов вычислений. Поэтому степень овладения вычислительными умениями зависит от четкости сформулированного правила и от понимания принципа его использования. Умение формируется в процессе выполнения целенаправленной системы упражнений. Очень важно владение некоторыми вычислительными умениями доводить до навыка.

Вычислительные навыки отличаются от умений тем, что выполняются почти бесконтрольно. Такая степень овладения умениями достигается в условиях целенаправленного их формирования. Образование вычислительных навыков ускоряется, если учащемуся понятен процесс вычислений и их особенности. При обучении вычислениям и совершенствовании техники счета необходимо отчетливо представлять, какие умения и навыки у учащихся необходимо сформировать.

При устных вычислениях надо помнить данные числа и законы действий над ними. При этом формирование навыков устных вычислений связано с выработкой навыка запоминания чисел, выявления особенностей отдельных чисел. Правила и приемы вычислений не зависят от того, выполняются они письменно или устно. Однако владение навыками устных вычислений представляет большую ценность не только потому, что в быту ими пользуются чаще, чем письменными выкладками, но и потому, что они ускоряют письменные вычисления, позволяют усовершенствовать их. Наличие у учащихся навыков устного счета влияет на степень отработки у них рациональных и безошибочных вычислительных умений. Например, без навыков устного использования таблиц сложения и умножения невозможно в совершенстве овладеть умениями в выполнении арифметических действий.

В 5–6 классах учащиеся овладевают навыками вычисления с натуральными и целыми числами, с обыкновенными и десятичными дробями. При этом алгоритмы вычислений с двух-трехзначными числами должны быть отработаны с учащимися до автоматизма. Все вычисления должны производиться достаточно бегло; их включение в выполнение более сложных вычислений не должно затруднять учащихся.

В 7–9 классах обобщаются и систематизируются сведения о действительных числах, развиваются и закрепляются вычислительные навыки. При этом не следует ослаблять внимание к поддержанию достаточно высокого уровня техники вычислений и повышению уровня вычислительной культуры учащихся. Эта задача должна решаться путем последовательного увеличения доли вычислений при изучении основного материала курса.

Вычислительным навыкам, как и любым другим, необходимо учить. Качество вычислительных умений и навыков определяется знанием правил и алгоритмов вычислений. Поэтому степень овладения вычислительными умениями зависит от четкости сформулированного алгоритма и от понимания принципа его использования. Очень важно владение некоторыми вычислительными умениями доводить до навыка. Что нужно сделать для этого учителю?

1. Ознакомить учащихся с принципом работы того или иного нового для них вычислительного алгоритма.

2. Провести работу по отработке отдельных операций, входящих в новый алгоритм. Для формирования навыка выполнения данного алгоритма недостаточно отдельных упражнений, необходима тщательно продуманная их система, в которой должна соблюдаться последовательность упражнений с постепенным их усложнением. Упражнения по формированию навыков должны быть достаточно разнообразными как по содержанию, так и по форме, лишь в этом случае достигается прочность навыков.

3. Провести работу по закреплению алгоритма – использовать его применение во всех стандартных и нестандартных ситуациях. Это немаловажно, так как уровень вычислительных навыков определяется систематичностью закрепления ранее усвоенных приемов вычислений и приобретением новых в связи с изучаемым материалом.

4. И, конечно же, необходимо провести проверку по усвоению алгоритма учащимися. Этому могут помочь проведение самостоятельных работ и наблюдения учителя за работой учащихся в классе. Анализ письменных и устных работ учащихся дает возможность установить, как усвоен данный материал, какие общие и наиболее характерные ошибки допущены при проведении вычислений, кто из учащихся и что именно не усвоил и как ликвидировать выявленные пробелы.

Таким образом, вычислительные навыки нужны и при изучении программного материала в школе, и в повседневной жизни. Кроме того, они окажутся полезными для прикидки ожидаемого результата не только в учебной деятельности, но и в жизни. Именно поэтому учить учащихся быстро, правильно и рационально считать в школе необходимо и не только на уроках, но и на внеклассных занятиях по математике.

Для достижения правильности и беглости устных вычислений на каждом уроке математики необходимо выделять 5–10 минут для проведения упражнений в устных вычислениях, предусмотренных программой каждого класса.

Устные упражнения – неотъемлемая часть урока математики. Они могут проводится как вначале урока, так и на любом его этапе. Остановимся на устных упражнениях, проводимых в начале урока. Наиболее часто устные упражнения – первый этап урока, причем не только в 5–6-х, но и в старших классах.

Цель этого этапа: во-первых, подготовить учащихся к продуктивной работе на всем протяжении урока, значит, среди этих упражнений должны быть задания на восстановление опорных заданий и умений. Во-вторых, постоянно проводить работу по поддержанию и совершенствованию ранее сформулированных знаний и умений, в частности, вычислительных навыков. И, в-третьих, способствовать развитию учащихся, т.е. необходимо на каждом уроке предлагать задачи, требующие сообразительности, внимания, анализа и обобщения имеющихся знаний и т.п. В 5–6 классах для развития и совершенствования вычислительных навыков часто используются так называемые цепочные вычисления, такие цепочки даются в виде схем и в виде столбиков. Роль этих упражнений не сводится только к поддержанию умения считать. Важно, что они хороши для развития оперативной памяти, тренировки внимания, настойчивости.

Рассмотрим часто встречающиеся случаи умножения и деления, в которых особенно плодотворно применение устного счета. (3)

1. Дроби.

Умножение целого числа на смешанное.

Умножение целого числа на смешанное число может быть выполнено по правилу умножения числа на сумму, так как смешанное число есть сумма целого числа и дроби. Поясним это на числовом примере:

Но при умножении целого числа на смешанное число можно обратить смешанное число в неправильную дробь, затем умножить целое число на числитель неправильной дроби, полученное произведение сделать числителем искомого произведения, знаменатель же произведения оставить знаменатель множителя:

Как видим, первый способ проще и дает возможность быстрее производить умножение.

Преимущество первого способа перед вторым в данном примере очевидно. Но могут быть случаи, когда проще и быстрее можно решить пример вторым способом:

Таким образом, при умножении целого числа на смешанное число надо внимательно рассмотреть пример и применить тот способ, который в данном случае быстрее ведет к цели.

Деление смешанного числа на целое.

Смешанное число можно рассматривать как сумму двух чисел. Следовательно, деление смешанного числа на целое есть деление суммы двух чисел на число. Чтобы разделить сумму чисел на число, достаточно разделить на это число каждое из слагаемых, и сложить полученные результаты.

Как видим, этот способ гораздо легче (он дает возможность быстрее производить вычисления), чем обычный способ деления смешанного числа на целое с образованием смешанного числа в неправильную дробь.

Рассмотрим на числовых примерах.

1) квадрат числа 11 равен 100 + (10+ 11)= 121;

2) квадрат числа 12 равен 121 + (11 + 12) = 144 и т.д.
Объяснение этого способа нахождения квадрата числа следующее:

(k + 1)² = k² + 2k • 1 + 1² = k² + [k + (k + 1)].

3) 75² = 5625.

4) 76² = (75 +1)² = 75² + [75 + (75 + 1)] = 75² + (75 + 76) = 5625 + 151 = 5776.

Получаем 76² = 5776.

2. Устное возведение в квадрат смешанных чисел.

Случаи возведения в степень смешанного числа по формулам сокращенного умножения.

а) Квадрат смешанного числа с дробью .

Чтобы возвести в квадрат смешанное число с дробью , достаточно умножить целую часть числа на число, единицей большее, и к произведению приписать .
Дано: число , где k – целое.

Доказать:

Доказательство: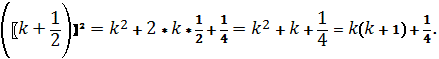

б) Квадрат смешанного числа с дробью .

Чтобы возвести в квадрат смешанное число с дробью , достаточно возвести в квадрат целую часть этого числа, затем прибавить ее половину и, наконец, к полученной сумме прибавить , если целая часть – четное число. Если же целая часть – нечетное число, то к квадрату целой части прибавляется половина числа, на единицу меньшего данной целой части смешанного числа, и к сумме прибавляется .

1) Дано: число , где k – четное число.

k , где k – четное число.

Доказательство: =

2) Дано: число k +, где k – нечетное число.

Доказать: (k +² = k² +  +

(в данном случае k’ на единицу меньше числа k)

Доказательство: k = k’ + 1, следовательно,

(k + )² = k² +  +  = k² +  +  +  = k² +  +

1) k – четное число

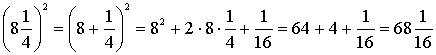
2) k – нечетное число

Как пишет педагог О.П. Зайцева в своей статье «Роль устного счета в формировании вычислительных навыков и развития личности ребенка» важность и необходимость устных упражнений доказывать не приходиться. Значение их велико в формировании вычислительных навыков и в совершенствовании знаний по нумерации, и в развитии личностных качеств ребёнка. Создание определённой системы повторения ранее изученного материала дает учащимся возможность усвоения знаний на уровне автоматического навыка. Устные вычисления не могут быть случайным этапом урока, а должны находиться в методической связи с основной темой и носить проблемный характер. Приемы быстрого счета позволят повысить качество обучения и уровень математических знаний учащихся. Они служат одним из средств предупреждения формализма в преподавании математических дисциплин, делают знания более действенными, гибкими и эффективными.

Литература:

1. Автайкина, А.К. Некоторые формы организации устного счёта / Математика в школе, №3/, 1991 г.

2. Борткевич Л.К. Повышение вычислительной культуры учащихся» / Математика в школе, №5/, 1995 г.

3. Глебов, И.И. Упражнения по привитию вычислительных навыков учащихся 5–9 классов средней школы, М.: Просвещение, 1959. – 66 с.
4.  Е.С. Канин, А.Я. Блох и др. Методика преподавания математики, М.: Просвещение, 1985г, 268 с.
5.  Ройтман, П.Б., С.С. Минаев, Н.С. Прокофьева и др., Повышение вычислительной культуры учащихся /пособие для учителей/, М.: Просвещение, 1985. – 48 с.