ОСОБЕННОСТИ ПРОГРАММЫ MАPLE В ИЗУЧЕНИИ КРИВЫХ ВТОРОГО ПОРЯДКА

Егембердиева Шынар Канатовна

Таразский Государственный университет имени М.Х. Дулати, Тараз

преподаватель, магистр

Жарылкасын Аяулым

Таразский Государственный университет ианрылкасымени М.Х. Дулати, Тараз

студент гр. Мат-215

В настоящее время разработано значительное число программных средств, которые широко используются для решения математических, технических, инженерных и учебных задач. Наиболее простыми для понимания учащихся являются пакет Maple. Как и другие подобные пакеты Maple может решать большое количество математических задач путем ввода команд без предварительного программирования. Кроме того, математический пакет Maple дает возможность повысить наглядность изучаемого материала, организовать исследовательскую деятельность студентов.

Maple-язык программирования считается одним из самых лучших и мощных языков программирования математических задач. Это, наряду с упомянутыми новыми средствами пакета Maplets, позволяют создавать высококачественные электронные уроки, статьи и даже целые книги.

Программа «Maple»- система компьютерной математики, способная

выполнять быстро и эффективно не только символьные, но и численные расчеты, причем сочетает это с превосходными средствами графической визуализации и подготовки электронных документов.

Данная тема достаточно сложна в изучении, поскольку требует высокого уровня мышления учащихся, а также наличия умений построения геометрических чертежей.

И так, геометрия как учебный предмет в ВУЗе дедуктивной, аксиоматической основе и требует для своего усвоения хорошо развитого теоретического, понятийного мышления.

Линии второго порядка определяются уравнениями вида

(1)

Основной метод исследования и классификации этих линий заключается в подборе такой декартовой прямоугольной системы координат, в которой уравнение линии имеет наиболее простой (канонический) вид, удобный для исследования. Чтобы проанализировать уравнение кривой, рассмотрим три случая:

1) (эллиптический случай);

2) (гиперболический случай);

3) (параболический случай).

После данного преобразования уравнение (1) примет вид:

(*)

Подробнее рассмотрим эллиптический случай. Из следует, что ,. Пусть A′ > 0, C′ > 0. Выделим полные квадраты при неизвестных x′, y′, получим:

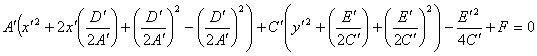(2)

Дополним члены, содержащие x’ и y’,до полного квадрата:

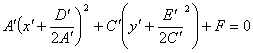(3)

где Положим, тогда уравнение (3) примет вид:

(4)

Пусть. Разделим обе части уравнения (4) на , получим:

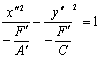(5)

Так как, то предположим, что

(6)

Из (5) и (6) следует, что мы получили каноническое уравнение эллипса

(7)

Эллипс - множество точек плоскости, для каждой из которых сумма расстояний до двух данных точек и этой плоскости, называемых фокусами эллипса, есть заданная постоянная величина, равная 2а, а > 0, большая, чем расстояние между фокусами 2с, с > 0. Общий вид уравнения

(8)

Пересечение эллипса с осями координат. Найдем точки пересечения эллипса с осью _. Пусть , тогда уравнение эллипса имеет вид: , следовательно Отсюда следует, что точки, являются точками пересечения с осью

Так как и разных знаков, следовательно , одна из скобок больше нуля, другая скобка меньше нуля. Пусть (9) тогда мы получаем каноническое уравнение гиперболы:

(10)

При уравнение принимает вид:

(11)

Пусть , тогда и уравнение (11 ) примет вид:

откуда 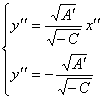(12)

Таким образом, получили уравнения двух пересекающихся прямых. Рассмотрим параболический случай. Так как , то.Пусть. Так как после поворота , то уравнение (*) преобразуется до вида:

(13)

Соберём члены, содержащие , и дополним их до полного квадрата:

тогда уравнение (13) примет вид: или

(14)

где. Из (14) следует, что Рассмотрим два случая. Пусть , тогда , то есть

(15)

где Положим , тогда уравнение (15) примет вид: Это каноническое уравнение параболы, симметричной относительно оси.

Пусть, тогда уравнение (14) перепишется в виде

(16)

1. Если , то получим уравнение оси .

2. Если , то возможны два случая. Если и одного знака, то точек, удовлетворяющих данному уравнению, нет; если же и разных знаков, то, где, поэтому 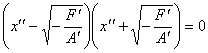и уравнение (16) описывает две параллельные прямые:

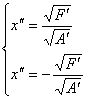
Пусть , тогда уравнение (*) примет вид

(17)

Если, а, то точек, удовлетворяющих уравнению (17), нет; если же или отличны от нуля, то уравнение (17) описывает прямую.

Вывод. Путем преобразований кривой второго порядка, определяемой уравнением (1) мы можем получить уравнения таких линии второго порядка, как:

1. - уравнение эллипса

2. - уравнение гиперболы

3. - уравнение параболы

4. 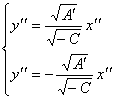_- совокупность двух пересекающих прямых

5. 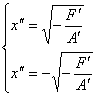_- совокупность двух параллельных прямых.

Окружность - множество точек плоскости, равноудаленных от данной точки М₀, называемой ее центром. Общий вид уравнений

Отношение называется эксцентриситетом окружности. Для окружности эксцентриситет окружности равен нулю. Частный случай эллипса – окружность., где радиус окружности.

Давайте постройм этих кривых через программу Маpl.

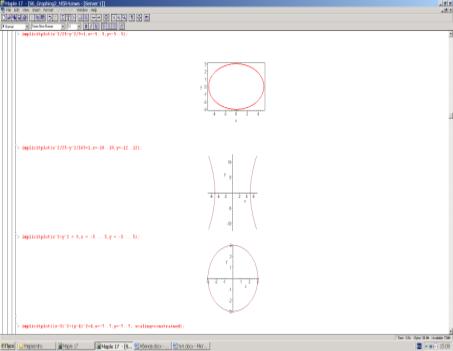
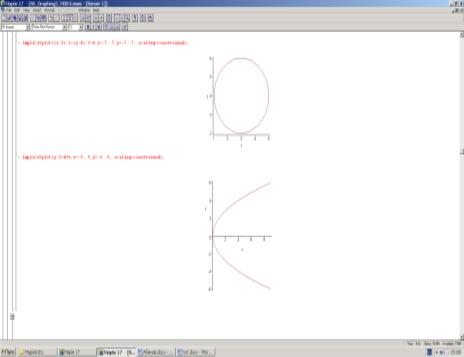
ЛИТЕРАТУРА

1. А.Д. Александров, Н.Ю. Нецветаев, Геометрия. «Наука» Физматлит, 1990 32-53

2. Метельский Н. В. Пути современного обучения математики. – Мн., 1989.

3. Бескоровайная Л. С., Перекатьева О. В. Методика современного открытого урока математики. – Ростов-на-Дону, 2003.

4. Новосельцева З.И. Развернутые планы лекций и учебные задания для студентов по курсу "Теоретические основы обучения математике"/ С.-Петербург, Изд-во "Образование", РГПУ, 1997

5. Методика преподавания математики в средней школе : Общая методика; Учебное пособие для студентов физико-математического факультета педагогических институтов / В.А. Оганесян, Ю.М. Колягин, Г.Л. Луканкин, В.Я. Саннинский, -2-е издание переработано и дополнено / М., Просвещение ,1980.