MATHEMATICS / 3. Applied mathematic

Candidate of Physical and Mathematical Science Iskakova A.

L.N. Gumilev Eurasian National University, Astana, Kazakhstan

Modeling of unbiased estimators for probabilities of the dynamics of the development of production in Europe

 

Comparing the path of each European country’s trend growth rate with the corresponding secular actual average growth, and our setting of a dating of growth cycles of industrial productivity in Europe, it raises interest in European industry and constitutes the basis for future poles of European knowledge, particularly in Kazakhstan.

To date, probabilistic models describing such situations were not considered. Extremely relevant example of application of such a model is the advertising industry, where it is necessary to link the distribution of consumer interests with appropriate advertisements in various sources. Similar problems are very common in meteorology and other fields. In this article we present statistical evaluation of the distribution of the sum of random values  L1, … , Ld, where L1, … , Ld are not observable and observable only their sum. Thus, the results of the proposed work can solve many of these problems.

Suppose that an urn contains balls and each ball in the urn marked some value Lα. Also assume that the number of possible Lα there is d.

Let the elements of the vector p = (p1, … , pd) determine the probability of retrieving the ball boxes labeled respective values ​​of   L1, … , Ld, and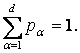 

Produces a sequence of extraction of n balls from the urn with the return, and it is not known exactly which balls were removed from the box. We only know the value of u, which represents the sum of the values ​​of the n taken out of the urn balls. To study this situation requires the construction of a probability distribution u.

Assume that Vu is the number of possible combinations r1vuL1,…, rd vuLd, which together formed  u, where r1vu,…, rdvu determine the possible number of balls are removed, that bear the L1, … , Ld. In other words, in [1] that is, the number of partitions Vu  u on the part of  L1, … , Ld.

The probability that the random variable U takes the value u, there

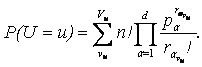                                      (1)

Theorem. A function that is defined in (1) is a probability distribution.

Let X = (X1, ..., Xk) represents a sampling volume of distribution n (1) and x =(x1, ..., xk)  is the observed value of  X, where the elements xi (i = 1, ..., k) represent the sum of the values ​​of the n balls consistently taken out of the urn with replacement. For each i = 1, ..., k we define the number of partitions of  Vi õi values ​​at L1, … ,Ld. Vectors r1i=(r11i,…,  rd1i), …, rVi=(r1Vi,…,  rdVi), defining these partitions, when vi=1,..., Vi, are solutions of the following system of equations

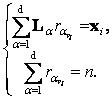                                            (2)

Suppose that for each  j = 1, ..., μ, where 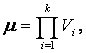 there exists a vector zj=(z1j,..., zdj), defined as  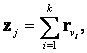 and the indices in the right and left side of the linked-to-one correspondence, which is not unique.

Lemma. a) If any element of the implementation of the sample x =(x1, ... , xk) of the distribution (1) has more than one partition on a view of the portion, the solutions z1, … , zμ, based on observation, not implementations are sufficient statistics .

b) If all the elements of the implementation of the sample x =(x1, ... , xk) of the distribution (1) have no more than one partition on a view of the portion, the solution  z1, based on observation, and is the only implementation of a complete sufficient statistic.

The following theorem, presented in the paper [6-9], to determine the set of unbiased estimates for the probability distribution of the test.

Theorem. The elements of  W(u, z)={W(u, z1), …, W(u, zμ)} is an unbiased estimate of the probability P (U = u) of the distribution (1) that for j = 1, ..., μ is defined as

                                         (3)

where Vu is the number of partitions of  u on the part of  L1,…, Ld; for each partition  r1vu,…, rdvu determine the possible number of  balls are removed, that bear the L1, …, Ld; k≥1 and zαj≥rαvu,  when α = 1, ..., d, vu=1, …, Vu.

 

REFERENCES

1.    AA Borovkov Mathematical Statistics. Parameter estimation. Testing hypotheses, M .: Nauka. 1984.- 472 p.

2.    AA Borovkov Probability theory, M .: Nauka. 1986.-431 p.

3.    Voinov VG, Nikulin, MS Unbiased estimators and their applications M .: Nauka. 1989. - 440 p.

4.    Iskakova AS On a class of discrete multivariate distributions generated urn scheme with balls labeled rectangular matrices. // Bulletin KazSU Ser. Mat., Mech., informatics. 2000 ¹1 (94). S. 16-20.

5.    AS Iskakova Determine the most suitable unbiased estimate for a weather forecast. // Siberian Journal of Industrial Mathematics. G.Tom 2002 V, 1 (9). S.79-84.