MATHEMATICS
/ 3. Applied mathematic
Candidate
of Physical and Mathematical Science
Iskakova A.
L.N. Gumilev Eurasian National University, Astana,
Kazakhstan
Statistical estimation
Rao-Blackwell-Kolmogorov method for model of sum of dynamics of the development of production in
Europe
Questions of dynamics
of the development of production in Europe as factors - economic
reection of reality, lately is global based on progressive changes in
urbanization of modern systems.
The basic mathematical result of this paper is based on the work [2-7],
where in [2-5] and [7] it was presented the new probabilities model of sum of
random variables, authors of [6] described a Rao-Blackwell-Kolmogorov method
for particular discrete probability model.
Any social benets received on job loss event is a consequence of the
inuence of group of factors. Assume that the social case was formed by m factors, which any factor has some
degree of action. Let's dene each factor as one of the possible numbers l1;
l2;
: : : ; lm with the appropriate values of the probabilities p1;
…; pm; and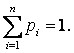 
Let the cosial case u
can form by n factors with possible return. And the factor l1 was inuenon the social case with timehe loss
of work time x r2 and so on factor lm was influenon
social case with timehe loss of work time x rm: It's obvious tha
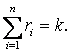Suppose we have
social case u; which presented as sum of n: I.e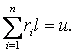 
The last formula is a formula
for the partition of u into parts l1; l2;… ;im the
number of partitions
Theorem 1 The probability that the sum of the numbers on the n factors aect
repetition on social occasions u; determined by the formula
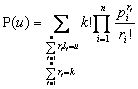(1)
Proof. Item of evidence. Needless to say, if there is a partition u to parts
l1; l2; : : : ; lm that the system of equations
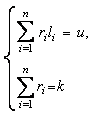
it has one or more solutions. The probability of each
partition u to l1; l2; : : : ; lm de_ned by the polynomial distribution. So, we
come to the proof of the theorem.
It is obvious
that in practice the elements of the vector are not known p = (p1; : : : ; pm).
Therefore, formula (1) does not _nd in the actual application. Thus, we need
the determining the probability of estimates (1). Let Õ=(X1, ..., Xk)is the sample, where its
elements have distribution (1) and its realization is vector õ=(x1,
..., xk) For each i=1, ..., k Vi defines number of
partitions of the element xi on l1;
l2;
: : : ; lm . Vectors r1i = (r11i
; : : : ; rm1i ); : : : ; rVi = (r1Vi
; : : : ; rmVi ) are the solutions
if for each j = 1; : : : ; _
where 
is a vector
zj=(z1j,..., zdj),
defined as
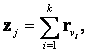(2)
and indexes in the left and right parts are
interconnected one-to-one correspondence,
which is not unique.
Theorem 2 The elements of set W(u; z) = {W(u; z1); : : : ;W(u; z_)} are an
unbiased estimations of the probability P(U = u) from distribution (1), which
de_ned as in case of j = 1; : : : ; µ
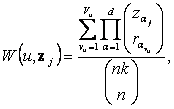(3)
where
Vu –partition
numbers u on parts l1,…, lm; for each partition r1vu,…, rdvu,determine the possible number of
influence factors l1, …, lm; k≥1 è zαj≥rαvu,
if α=1,…, d, vu=1, …, Vu.
Reference
1 Abrams M. Mechanistic social probability: How
individual choices and varying circumstances produce stable social patterns. _
2012.
2 Chichagov V. V. On Asymptotic Behavior of Unbiased
Probability Estimators for Lattice Distributions with the Mean as a Su_cient
Statistic //Journal of Mathematical Sciences. _ 2013. _Ò. 189. _ . 6.
3 Ayman I. Statistical Research for Probabilistic
Model of Distortions of Remote Sensing //Journal of Physics: Conference Series.
_ IOP Publishing, 2016. _ Ò. 738. _ . 1. _ Ñ. 012004.
4 Ayman I. Construction of the most suitable unbiased
estimate distortions of radiation processes from remote sensing data //Journal
of Physics: Conference Series. _ IOP Publishing, 2014. _ Ò. 490. _ . N 1. . 012113.
5 Bordeaux V. S. Unbiased Estimation in Reliability
and Similar //Recent Advances in Reliability Theory: Methodology, Practice, and
Inference. _ 2012. _ Ñ. 435.
6 Bordes L., Nikulin M., Voinov V. Unbiased estimation
for a multivariate exponential whose components have a common shift //Journal
of multivariate analysis. _ 1997. _ Ò. 63. _ . 2. _ Ñ. 199-221.
7 Iskakova A. S. Determination of the most suitable
unbiased estimate for a weather forecast being correc //Sibirskii Zhurnal
Industrial'noi Matematiki. _ 2002. _ Ò. 5. _ . N 1. 79-84.