К. ф.-м. н. Сериков В.И., к. ф.-м. н. Воронин С.В.
Липецкий государственный технический университет, Россия
Особенности метода псевдопотенциалов,
связанные с обобщёнными уравнениями Бюргерса.
Метод псевдопотенциала
является эффективным средством для поиска решений обобщенных уравнений
Бюргерса. В работе [1] он применяется к 1+1 -
мерному уравнению. Ниже мы
развиваем этот метод для 3+1 – мерного обобщённого уравнения Бюргерса, как при
отсутствии, так и при наличии внешнего силового поля.
Обобщённое уравнение
Бюргерса имеет вид [2]
 . (1)
. (1)
Введём новые функции qi
(i=1,2,3…N) и запишем систему дифференциальных уравнений первого порядка
в виде
![]() ,
(2)
,
(2)
![]() . 3)
. 3)
Векторный характер
величин ![]() определяется 3-мерным
оператором
определяется 3-мерным
оператором ![]() , 3- вектором является
также и величина
, 3- вектором является
также и величина ![]() , тогда как величина q является
вектором N-мерного пространства. Градиент в этом пространстве в дальнейшем
обозначается
, тогда как величина q является
вектором N-мерного пространства. Градиент в этом пространстве в дальнейшем
обозначается ![]() ,а основное требование теории псевдопотенциала для системы
уравнений (2,3) имеет вид:
,а основное требование теории псевдопотенциала для системы
уравнений (2,3) имеет вид:
![]() ,
4)
,
4)
Поскольку в методе
псевдопотенциала функции ![]() ,
,![]() ,
,![]() ,… задаются независимо в некоторой точке, то производная
,… задаются независимо в некоторой точке, то производная ![]() локально не зависит от
перечисленных величин и, поэтому, необходимым условием выполнения (4) является
локально не зависит от
перечисленных величин и, поэтому, необходимым условием выполнения (4) является
![]() .
(5)
.
(5)
Исключение также членов, содержащих
вторые производные ![]() , приводит к требованию
, приводит к требованию
![]() , (6)
, (6)
откуда следует
![]() . (7)
. (7)
Требование того, чтобы в
уравнении (4) коэффициент при ![]() (т.е.
(т.е. ![]() ) равнялся
нулю, приводит к соотношению
) равнялся
нулю, приводит к соотношению
![]() .
(8)
.
(8)
Приравнивая в (4) к нулю
коэффициент при ![]() , после интегрирования получаем
, после интегрирования получаем
![]() . (9)
. (9)
В [1] показано, что, при
существовании псевдопотенциала, всегда существует возможность построить
линеаризованный потенциал. Поэтому зависимости (8) и (9) можно записать в форме
![]() , (10)
, (10)
![]() . (11)
. (11)
C использованием (10), имеем
![]() . (12)
. (12)
Используя (7, 10, 12) в (4) и
приравнивая к нулю коэффициенты при соответствующих величинах, получаем систему
матричных уравнений
![]() , (13)
, (13)
![]() , (14)
, (14)
![]() . (15)
. (15)
Наиболее простое решение
системы уравнений (13, 14, 15) для индексов, пробегающих значения i,k,m=1,2,3
имеет вид
![]() , (16)
, (16)
так, что соотношения (10) и (12)
принимают вид
![]() , (17)
, (17)
![]() ,
, ![]() . (18)
. (18)
А соотношение (7) можно представить в
форме
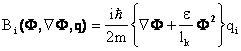 .
(19)
.
(19)
С учётом соотношений (17)
и (19) дифференциальные уравнения первого порядка (2) и (3) принимают вид
![]() ,
(20)
,
(20)
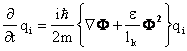 , (21)
, (21)
для N=1 уравнения можно записать в форме
![]() , (22)
, (22)
из которой следует, что можно
рассматривать как потенциал и
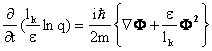 . (23)
. (23)
Применяя к уравнению (23)
оператор ![]() , используя
уравнение (22) в левой части, представляющее собой преобразование Хопфа-Коула,
приходим к уравнению Бюргерса-Шрёдингера. Использование преобразования (22) в
правой части уравнения (23) приводит к уравнению Шрёдингера для свободной
частицы.Рассмотрим теперь обобщённое уравнение Бюргерса отвечающее уравнению Шрёдингера в силовом
поле . Уравнение Бюргерса запишем в виде
[3]
, используя
уравнение (22) в левой части, представляющее собой преобразование Хопфа-Коула,
приходим к уравнению Бюргерса-Шрёдингера. Использование преобразования (22) в
правой части уравнения (23) приводит к уравнению Шрёдингера для свободной
частицы.Рассмотрим теперь обобщённое уравнение Бюргерса отвечающее уравнению Шрёдингера в силовом
поле . Уравнение Бюргерса запишем в виде
[3]
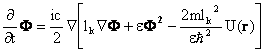 . (24)
. (24)
Cистему дифференциальных уравнений
первого порядка запишем в форме
![]() ,
(25)
,
(25)
![]() .
(26)
.
(26)
Функция ![]() является в этом случае
однокомпонентной, т.е. отвечает пространству с N=1. Основное требование теории
псевдопотенциала
является в этом случае
однокомпонентной, т.е. отвечает пространству с N=1. Основное требование теории
псевдопотенциала ![]() и применение
рассмотренного выше метода приводит к уравнению
и применение
рассмотренного выше метода приводит к уравнению
![]() , (27)
, (27)
где ![]() ,
,![]() , тогда из (27) имеем
, тогда из (27) имеем
![]() . (28)
. (28)
После этого система
дифференциальных уравнений первого порядка (25, 26) принимает вид
![]() ,
(29)
,
(29)
где ![]() , как и выше в (21),
, как и выше в (21),
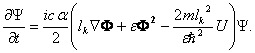 (30)
(30)
Если в заданном силовом
поле ![]() рассматривать для уравнения Шрёдингера задачу
на собственные значения, то, с учётом разделения переменных имеем
рассматривать для уравнения Шрёдингера задачу
на собственные значения, то, с учётом разделения переменных имеем
![]() ,
(31)
,
(31)
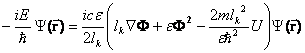 . (32)
. (32)
Исключение ![]() из уравнения (32) при помощи (31) приводит к
стационарному уравнению Шрёдингера
из уравнения (32) при помощи (31) приводит к
стационарному уравнению Шрёдингера
![]() . (33)
. (33)
В 1+1- мерном случае
можно рассмотреть стационарное уравнение Шрёдингера с модифицированным
потенциалом Пешля – Теллера [5]
![]() . (34)
. (34)
Значениям параметра ![]() отвечают
решения типа стоячих волн. Для отрицательного значения γ имеем
отвечают
решения типа стоячих волн. Для отрицательного значения γ имеем
![]() , (35)
, (35)
а для положительного значения имеем
![]() . (36)
. (36)
Соответствующие решения
обобщённого уравнения Бюргерса находятся с помощью (31) и имеют вид
![]() , для
, для![]()
![]() для
для ![]() . . (37)
. . (37)
В заключение отметим, что в уравнении
типа (32) можно выбрать потенциальную энергию вида ![]() и записать пару
уравнений
и записать пару
уравнений
![]() ,
(38)
,
(38)
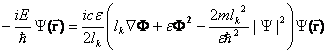 , (39)
, (39)
в которых исключение функции ![]() приводит к кубическому уравнению
Шрёдингера
приводит к кубическому уравнению
Шрёдингера
![]() . (40)
. (40)
Литература:
1. Абловиц М. Солитоны и метод обратной
задачи [Текст]:/ М. Абловиц, Х. Сигур. Солитоны и метод обратной задачи. Пер. с
англ., М.: Мир, 1987. – 479 с., ил.
2. Сериков В.И. Иерархия волновых
уравнений от обобщения уравнения Бюргерса к уравнениям квантовой теории
[Текст]:/В.И.Сериков, С.В. Воронин, О.А. Воронина// Veda a Technjljgie: Krok do
budoucnosti-2014: Материалы X научно – практической конференции (27.02.2014 –
05.03.2014). Т.29. – Praha, 2014. – С.77 – 81.
3.
Сериков
В.И. Квантовый подход к построению трёхмерного уравнения Бюргерса [Текст]:/
Сериков В.И.,Воронин С.В.Prospekts of world science,-2015: Materials of the XI
International scientific and practical conference. Volume 9.
Physics. Modern information technologies. Sheffield, Science and education LTD,
2015.
4. Миура Роберт М. Уравнение Кортевега –
Вриза – модельное уравнение для нелинейных волн в средах с дисперсией.
[Текст]:/ в сб. Нелинейные волны, под ред. С.Лейбовича и А.Сибасса, пер с англ. М. «Мир» 1977. –
319 с.
5. Флюгге З. Задачи по квантовой
механике, т.1[Текст]:/ З.Флюгге, Задачи по квантовой механике. Пер. с англ.,
М.: Мир, 1974. – 341 с.