Д. т. н. Бакиров Ж.Б., к. т. н. Танирбергенова А.А.
Карагандинский
государственный технический университет, Казахстан
Казахский
агротехнический университет им.С.Сейфуллина, Казахстан
ОПРЕДЕЛЕНИЕ НАДЕЖНОСТИ КОНСТРУКЦИЙ
ПРИ РАВНОМЕРНОМ РАСПРЕДЕЛЕНИИ НАПРЯЖЕНИЙ
Одной из важных проблем технических наук остается оценка надежности
элементов конструкций и технических систем. Это связано как с несовершенством
существующих методов расчета и норм надежности так и с усложнением условий
работы и повышением ответственности технических систем. В настоящее время многие задачи теории надежности
не доведены до решения, необходимого для практического применения. Поэтому совершенствование
и развитие расчета надежности упругих систем имеет большое практическое
значение и представляет собой важную научную проблему.
Вопросы расчета надежности технических систем рассмотрены в работах А.Р.
Ржаницина, В.В. Болотина и других и подробно изложены в монографии [1].
Определение надежности элементов конструкций при действии случайных напряжений
и случайных прочностных характеристиках материала рассмотрено в работе [2]. В развитие этих исследований в данной
работе рассмотрен расчет надежности элементов конструкций, когда расчетное
(эквивалентное) напряжение имеет равномерное распределение, а предельное
напряжение имеет различные законы распределения fR(R).
Равномерное распределение имеет следующую плотность вероятности:
при a<x<b; 
;
и функцию распределения
; 
и F(x)=1 при
.
Запишем выражение для вероятности
отказа [2]
.
Вероятность
безотказной работы, трактуемая нами как надежность, с учетом функции распределения
напряжения примет вид:
.
Отсюда 
.
(1)
а) Пусть предельное напряжение имеет нормальное распределение. Тогда
,
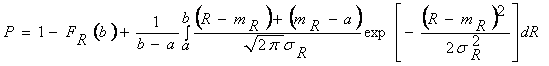где mR и σR - математическое ожидание и стандарт
случайной величины.
Введем обозначения: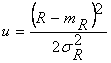 
; 
; 
;
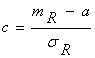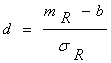и запишем
,
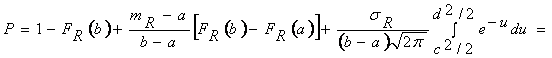
где Ф(х) - табулированная функция нормального
распределения [3].
Отсюда
следует 
.
б) Пусть предельное напряжение имеет логарифмически нормальное
распределение 
.
Интеграл в (1) обозначим через J и запишем
. (2)
Вычислим
интеграл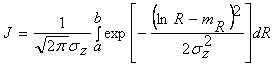 
.
Производя замену
переменных 
, перепишем
,
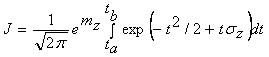где 
, 
.
Используя
известный интеграл [3]
,
запишем 
.
Учитывая, что
для этого распределения 
, получаем
.
Подставляя это
выражение в (2), находим надежность
.
в) Пусть предельное напряжение подчиняется гамма-распределению
,
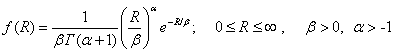где 
,
- параметры
распределения; Г(а) - полная гамма-функция.
Функция распределения этого закона
имеет вид [2]
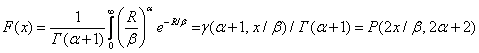, (3)
где γ(а,
х) - неполная гамма-функция; Р(х, а) - функция "хи-квадрат"
распределения. Все эти функции табулированы [3].
Тогда интеграл в
(2) примет вид
.
С учетом функции распределения и
выражения (2), получим
,
.
г) Пусть предельное напряжение распределено по закону Вейбулла
,
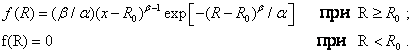где 
,
, 
- параметры
распределения.
Здесь надо рассмотреть три случая: 
; 
; 
.
В первом случае 
.
Производя замену
переменных 
, запишем
, 
, 
.
Подставляя эти
соотношения в интеграл и учитывая далее (3), получим
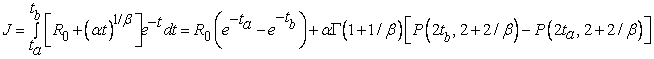
где 
, 
.
Подставляя все в
формулу (2), получим
.
Во втором случае нижний предел в интеграле 
нужно заменить на . Тогда в последнее выражение нужно подставить 
. Следовательно
.
При получаем 
.
Литература
1.
Бакиров Ж.Б. Вероятностные методы
расчета элементов конструкций. Караганда: КарГТУ, 2001. - 180 с.
2.
Капур К., Ламберсон Л. Надежность и
поектирование систем. – М.: Мир, 1980. – 604 с.
3. Справочник по специальным
функциям / Под ред. М. Абрамовица и И Стиган. М.: Наука, 1979. -830 с.