Технические науки / 6.Электротехника и радиоэлектроника.

Шумай Т.А., к.т.н. Черных А.Г.

Иркутский государственный аграрный университет, Россия

РАСЧЕТ ТРЕТЬЕЙ ГАРМОНИКИ В ТРЕХФАЗНЫХ ЧЕТЫРЕХПРОВОДНЫХ СЕТЯХ ПРИ ПЕРИОДИЧЕСКИХ НЕСИНУСОИДАЛЬНЫХ ВОЗДЕЙСТВИЯХ

При расчете электрических цепей с сосредоточенными параметрами при периодических несинусоидальных воздействиях, входном сигнал предварительно представляется в виде суммы гармонических составляющих, определяемых соответствующим рядом Фурье.

Повышение точности расчета напрямую связанно с числом гармонических составляющих (порядковым номером гармоник), входящих в указанную сумму. В большинстве практических случаев гармоника с порядковым номером три - входит в указанную сумму.

Использование символического метода позволяет существенно упростить проводимые расчеты путем перехода от интегро-дифференциальных уравнений электрического равновесия к соответствующим алгебраическим уравнениями с комплексными коэффициентами. Кроме того правильность самих расчетов может быть проверена аналитически путем составления уравнений баланса мощностей и графически путем построения векторных диаграмм токов и напряжений.

В качестве примера рассмотрим симметричный трехфазный генератор обмотки которого соединены в соответствии с изображением на (рис. 1) и являются источниками несинусоидальной системы трехфазных э.д.с. Мгновенное значение э.д.с фазы А задано в виде графика (рис. 2). Параметры фаз нагрузки, соединительных линий и э.д.с генератора равны:

Um=100В, Т=0,015с, L=7,5мгн, C=37,5мкф, R=5Ом, R0=4Ом.

Вычислим электрические величины и параметры, связанные с данной цепью применительно к третьей гармоники токов и напряжений.

b

1) Разложим функцию ЭДС eA(t) в ряд Фурье:

Сигнал – периодическая функция с периодом 2π определена следующим образом:

e_A(t) = - А_m при -π ≤ e_A(t) ≤ 0; e_A(t) = А_m при 0 ≤ e_A(t) ≤ π

учитывая, что функция e_A(t) нечетная, то постоянная составляющая отсутствует. Вычислим коэффициенты Фурье:

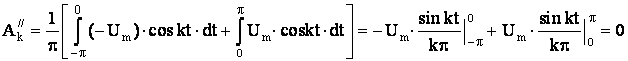
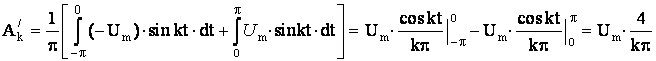
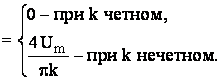
С учетом отсечения высших гармоник с порядковым номером выше семи имеем

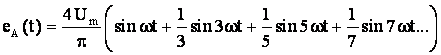
Комплекс действующего значения ЭДС E_A³ для третьей гармоники:

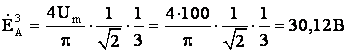
Реактивные сопротивления катушек индуктивности и конденсаторов для третьей гармоники:

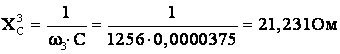
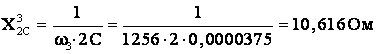
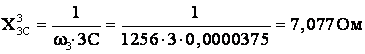
где

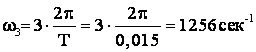
Расчет цепи начинаем с внесения сопротивлений Z_лА, Z_лВ, Z_лС линейных проводов в фазы приемника, в результате чего получаем упрощенную схему (рис. 3) с эквивалентным приемником, проводимости фаз которого равны

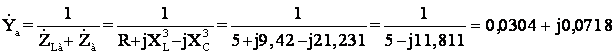
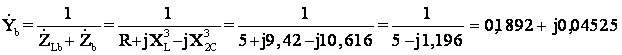
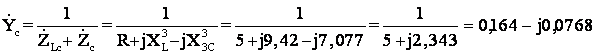
Проводимость нейтрального провода обозначим, как Y_nN имеем

Учитывая, что э.д.с фазы А для третьей гармоники определяется выражением

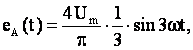
вычислим мгновенные значения э.д.с в фазах В и С, имеем

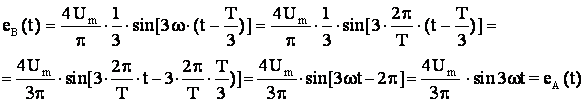
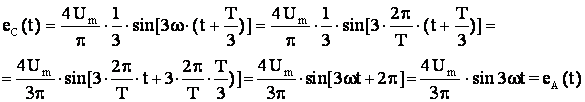
Поскольку при построении векторных диаграмм токов и напряжений для трехфазной цепи принята система координат в осях (+1, +j) ориентированная по вектору линейного напряжения U_AВ (см. рис. 3), то для данной системы координат с учетом последних соотношений напряжения для третьей гармоники в фазах источника определяться выражениями

Определим напряжение между нейтральными точками

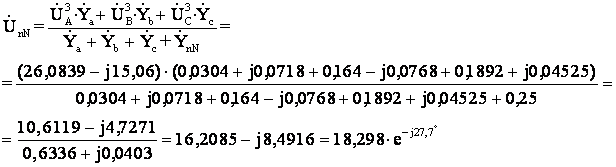
Определим комплексы напряжений U^|_а, U^|_в, U^|_с на эквивалентном приемнике через заданные фазные напряжения источника и напряжение U^|_nN :

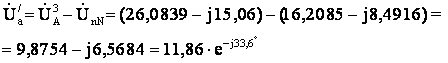
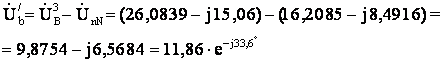
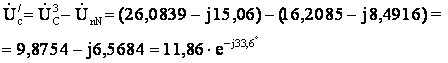
Выразим фазные токи и ток в нейтральном проводе через соответствующие проводимости и напряжения

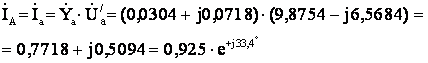
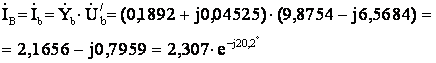
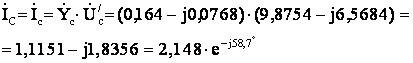
Проверка:

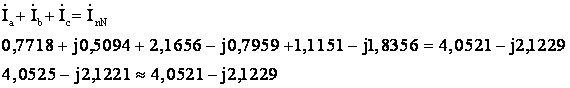
Определяем падения напряжения в проводах линии передачи

Определяем напряжения на фазах приемника

Вычислим напряжение U_bc

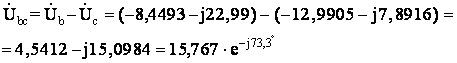
Определяем напряжения на нейтральном проводе

Определяем фазные коэффициенты мощности нагрузки:

j_а = j_uа- j_iа = -56,6⁰- 33,4⁰ = - 90,0⁰;

j_в = j_uв - j_iв = -110,2⁰-(-20,2⁰ ) = - 90,0⁰;

j_с = j_uс - j_iс = -148,7⁰-(-58,7⁰ ) = - 90,0⁰

Соответственно, cosj_а=0; cosj_в=0; cosj_с=0.

Определяем разность фаз между током и напряжением в фазах линии передачи

j_ал = j_uлА - j_iа = 95,4⁰-33,4⁰ = 62,0⁰;

j_вл = j_uлВ - j_iв = 41,8⁰- -(-20,2⁰ ) = 62,0⁰;

j_сл = j_uлС - j_iс = 3,3⁰-(-58,7⁰ ) = 62,0⁰

Соответственно, cosj_ал= cosj_вл = cosj_сл =0,4695

Определяем разность фаз между током и напряжением в нейтральном проводе

j_nN = j_unN - j_inN = -27,7⁰ - (-27,7⁰) =0⁰

Комплексные мощности фаз нагрузки равны

т.к S_а= P_а+j Q_а , то P_а=0 Вт; Q_а=18,1605Вар; S_а=18,1605 В×А

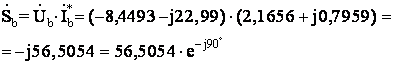
P_в=0 Вт; Q_в=56,5054 Вар; S_в=56,5054 В×А

P_с=0 Вт; Q_с=32,6496 Вар; S_с=32,6496 В×А

Комплексные мощности фаз линии передачи равны

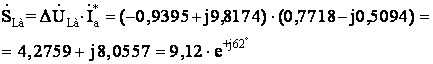
P_ал=4,2759 Вт; Q_ал=8,0557 Вар; S_ал=9,12 В×А

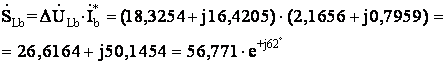
P_вл=26,6164 Вт; Q_вл=50,1454 Вар; S_вл=56,771 В×А

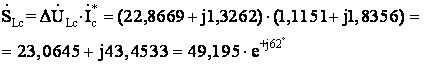
P_сл=23,0645 Вт; Q_сл=43,4533 Вар; S_сл=49,195 В×А

Комплексная мощность нейтрального провода равна

P_nN=83,7049 Вт; Q_nN= 0 Вар; S_nN=83,7049 В×А

Комплексные мощности фаз источника равны

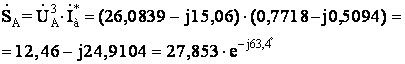
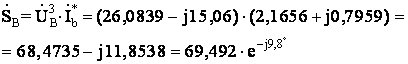
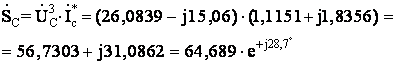
Проверка уравнения баланса полной мощности

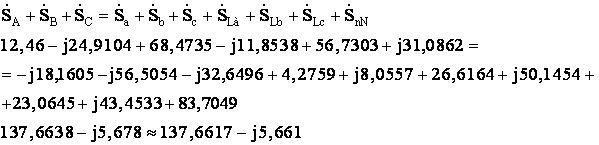
Полученный результат показывает:

– активная мощность трехфазного потребителя P =137,6617 Вт

– реактивная мощность имеет емкостной характер и равна Q =5,661 Вар

Модуль комплексной мощности S определяет полную мощность трехфазного несимметричного потребителя для третьей гармоники.

Векторная диаграмма токов и напряжений приведена на рис. 4.

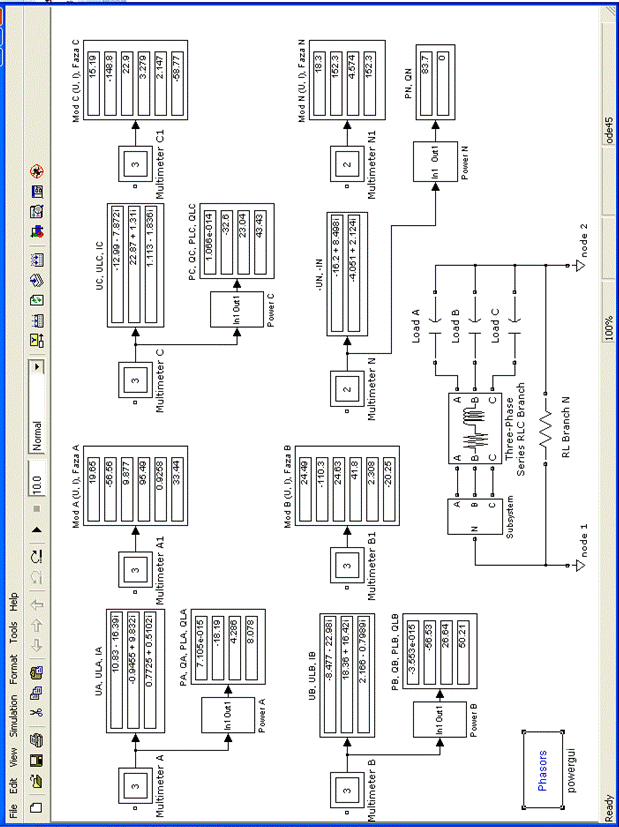
Схема модели электрической цепи (рис. 1) при входном воздействии (рис. 2) для третьей гармоники, полученная с использованием среды MatLab-SIMULINK представлена на рис. 5.

Рис. 5

Литература:

1. Черных А.Г. Электротехника и основы электроники; практикум по дисциплине: учеб. пособие / А.Г. Черных. – Иркутск: ИрГСХА , 2010. – 272 с.