Вржащ Е.Э.

Иркутский государственный аграрный университет, Россия

Математическая оптимизация эксперимента при нитроцементации стали в электростатическом поле

Методы математического планирования эксперимента достаточно известны и применяются в инженерной практике [3]. Однако возможности данного направления еще не раскрыты полностью, особенно его сторона, связанная с решением т.н. компромиссных инженерных задач.

В качестве примера рассмотрим технологическую задачу получения на поверхности стальных деталей диффузионного слоя, обладающего одновременно высокой твердостью и износостойкостью. Данную задачу можно полагать компромиссной, т.к. обычно образцы с высокой твердостью являются достаточно хрупкими и быстро изнашиваются. Особенно это характерно для процессов азотирования и нитроцементации, в которых участвует азот, химический элемент, придающий упрочняемым изделиям, с одной стороны, повышенную твердость, а с другой стороны, - хрупкость.

Для этого рассмотрим процесс высокотемпературной нитроцементации в электростатическом поле (ЭП) [1,4] с целью получения в поверхностной зоне стали качественного диффузионного слоя, достаточно глубокого, твердого и износостойкого. При этом в качестве переменных были выбраны шесть технологических факторов: x₁ – расход пропан-бутановой смеси (как главного поставщика углерода в образец); x₂ – расход аммиака (как главного поставщика азота); x₃ – температура процесса; x₄ – длительность процесса; x₅ – напряжение на электродах; x₆ – знак потенциала на образце. Параметрами процесса являлись: y₁ – поверхностная твердость образца по Виккерсу; y₂ – износостойкость; y₃ – глубина нитроцементованного слоя.

То есть была поставлена конкретная инженерная задача: на основании многофакторного технологического эксперимента нужно получить качественный диффузионный слой на образце, который должен обладать оптимальными эксплуатационными свойствами.

Чтобы решить такую задачу можно пойти двумя путями: осуществить классический эксперимент и при помощи метода проб и ошибок, интуиции и накопленного опыта на основании большого числа экспериментов получить соответствующие результаты. Математическая статистика такой путь называет пассивным. Но можно использовать активный, кибернетический подход, идею т.н. черного ящика. Что автором и было выбрано.

Обычно активные методы основываются на построении уравнения регрессии вида

,

где: y – параметр процесса (например, какое-нибудь свойство), x – факторы, влияющие на этот параметр, b – коэффициенты регрессии.

При этом требуется так поставить эксперимент, чтобы при минимальном количестве опытов, варьируя значение переменных по специально сформулированным правилам, найти область оптимума и получить ее математическую модель.

В нашем случае нитроцементацию в ЭП можно считать шестифакторным процессом и для полного его реализации требуется 2⁶ = 64 опыта. Был проведен дробный эксперимент вида 2^6-3 с построением 1/8 – реплики от полного эксперимента, т.е. выполнено 8 опытов. В работах [5,6] приведены исходные данные и результаты этого планирования.

На первом этапе исследования уравнения регрессии оказались следующими:

y₁ = 654 +5.6x₁ – 17.4x₃ – 13.9x₆,

y₂ = 207 – 22.2x₁ +14.0x₂ +29.3x₅ +13.2x₆,

y₃ = 0.64 +0.05x₃.

Эти уравнения являются линейными, при этом часть коэффициентов данных уравнений оказалась статистически незначимой.

Проверка адекватности уравнений по критерию Фишера показала, что при 95%-доверительной вероятности уравнения для у₁ и у₂ оказались адекватными, а для у₃ – нет. То есть полученные математические модели затрудняют интерпретацию экспериментальных данных. Кроме того, следует обратить внимание, что параметры оптимизации y₁, y₂, y₃ – то есть твердость слоя, его износостойкость и глубина слоя не всегда коррелируют между собой.

Твердый слой может быть хрупким и не износостойким и, наоборот, износостойкий слой не всегда бывает твердым. Возникает компромиссная задача: нужно получить достаточно глубокий диффузионный слой, обладающий одновременно высокими физико-механическими характеристиками по твердости и износостойкости.

Для выработки стратегии дальнейшего поиска необходимо было перейти ко второму этапу исследований: поиску единого, обобщенного критерия оптимизации, сводящему все параметры оптимизации, в том числе антагонистические, к единому комплексному параметру. Таким параметром может служить т.н. обобщенная функция желательности, которую ввел Харрингтон и величина которой меняется от 0 до 1, а параметр имеет определенную шкалу [3]. Таким образом, в выбранном интервале можно разработать шкалу для любого количества параметров оптимизации, а по ним определить их желательности.

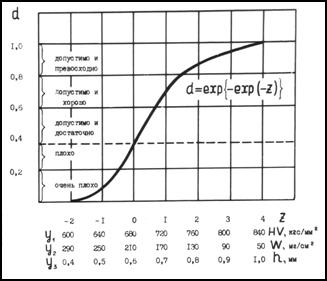
Рис.1. Функция Харрингтона и шкала «желательности» поверхностной твердости HV, износостойкости W и глубины слоя h в задаче поиска качественного нитроцементованного слоя

После определения желательности для каждого из свойств (в нашем случае d₁ - поверхностной твердости, d₂ - износостойкости и d₃ - глубины слоя) вводят обобщенную функцию желательности, которая определяется как среднее геометрическое "желательностей" отдельных свойств.

Обобщенная функция желательности в нашем случае рассчитывается при помощи формулы

При этом при значении параметра z=0 на графике (рис.1) наблюдается точка перегиба, и этот уровень может служить техническим уровнем (для него d=0,37). Следовательно, можно считать, что экспериментатора будут удовлетворять все свойства, имеющие d>0,37.

Обобщенная математическая линейная модель процесса нитроцементации в ЭП имеет вид

у=d=0.24+0.04х₁ –0.04х₂ -0.04х₃ +0.05х₄ -0.07х₅ -0.08х_6.

Она является адекватной при 95%-доверительной вероятности и имеет все шесть статистически значимых коэффициентов при варьируемых факторах.

Интерпретация уравнения показывает, что для достижения более качественного нитроцементованного слоя, необходимо увеличение значений факторов х₁, х₄ (соответственно расхода пропан-бутановой смеси и длительности процесса) и уменьшение значений факторов х₂, х₃, х₅ (соответственно расхода аммиака, температуры процесса и напряжения на электродах). Качественный фактор х₆ (знак потенциала на образце) при этом должен оставаться на нижнем уровне, т.е. иметь знак "минус".

Полученное линейное уравнение удовлетворительно описывает процесс нитроцементации в ЭП и позволяет достигнуть "почти стационарной области" при помощи метода крутого восхождения Бокса-Уилсона [3,5,6], приводящего к т.н. «почти стационарной области». Более подробная интерпретация этой области при помощи квадратичных коэффициентов регрессии привело к графику (рис.2), на котором координаты точки С показывают наиболее оптимальные газодинамические параметры выбранного технологического процесса.

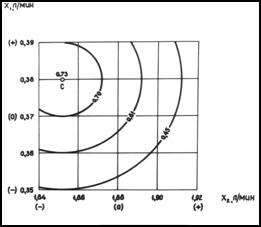
Рис. 2. «Почти стационарная» область процесса

нитроцементации в ЭП

Таким образом, можно считать, что центром "почти стационарной области" будет точка с натуральными координатами х₁=0.37л/мин, х₂=1.88л/мин, х₃=850⁰С, х₄=2 часа, х₅=1700В, х₆="-".

Полученные данные позволили выбрать оптимальные режимы обработки, позволяющие получить на детали качественный диффузионный слой. Квадратичная математическая модель несколько поправляет линейную по факторам х₁ и х₂, что позволило улучшить физико-механические и эксплуатационные свойства обрабатываемых деталей по сравнению со стандартными, так называемыми пассивными экспериментами [2].

Выводы:

При разработке различных технологических процессов обработки деталей машин и механизмов, в том числе сельскохозяйственного назначения, весьма перспективным являются методы математического планирования эксперимента, позволяющие не только значительно уменьшать число опытов, но и находить оптимальные технологические параметры обработки стальных изделий, в том числе для компромиссных инженерных задач. В работе построена математическая модель процесса нитроцементации в электростатическом поле, позволяющая рассчитать и практически внедрить оптимальные технологические параметры процесса для получения в поверхностной зоне стали качественного диффузионного слоя, достаточно глубокого, одновременно твердого и износостойкого. Натурные испытания упрочненных образцов подтвердили теоретические расчеты.

Список литературы

1. Вржащ Э.И., Вржащ Е.Э. Химико-термическая обработка в электростатическом поле. МиТОМ, 1983, № 3, с. 4-6.

2. Вржащ Е.Э., Юцис Е.Т. Сравнительный анализ структуры, фазового состава и механических свойств нитроцементованного слоя, образованного при обычных условиях и в электростатическом поле.//Сельскохозяйственные и прикладные науки в развитии сельского и лесного хозяйства: актуальные вопросы, практика и обмен опытом: материалы междунар. научн.–практ. конф., 6-11 июня 2006 г. – Иркутск, ИрГСХА, 2006. – С.294-298.

3. Новик Ф.С. Математические методы планирования эксперимента в металловедении, разд. I-IV. – М., МИСиС, 1969-1971.

4. E. Vrzhashch, G. Jozefaciuk, A.Suchaeva. The physical and technical principles of steel nitrocementation in electrostatic fields at superficial hardening of metals’ details. International Conference “Engineering problems in agriculture and industry”/June 2-4, 2010. Ulanbaatar, Mongolia, pp.57-61.

5. Вржащ Е.Э. Математическое планирование эксперимента при решении компромиссных инженерных задач на примере получения качественного диффузионного слоя при нитроцементации стальных изделий в электростатическом поле//Актуальные вопросы технического, технологического и кадрового обеспечения АПК: Материалы VI научн.-практ. Конф.с междун. участием «Чтение И.П. Терских». Иркутск: Изд-во ИрГСХА, 2014, с.21-26.

6. Wrzaszcz E. Mathematic design of an experiment at the optimization of nitrocementation in the electrostatic field./Materiały II Międzynarodowej Konferencji Naukowej - Agrolaser 2003. Lublin 2003. - S.93-96.