ОПТИМИЗАЦИОННЫЕ
ЗАДАЧИ
ПРИ
КОМПЕТЕНТНОСТНОМ ПОДХОДЕ
ПОДГОТОВКИ СТУДЕНТОВ
СТРОИТЕЛЬНОГО ВУЗА
Полежай
Е.А., Гарькина И.А.
Пензенский
государственный университет архитектуры и строительства
Математика
рассматривается как единая дисциплина, разделы которой взаимосвязаны и взаимозависимы;
является одной из основных, связанных с универсализацией математического
мышления, способствующих взаимопроникновению математики, науки, техники,
технологии, экономики и производства. При решении большинства практических задач
осуществляется перенос методов исследования из одной отрасли в другую, что
позволяет организацию междисциплинарных исследований [1…3].
Рассмотрим ряд задач
линейного программирования для формирования
компетенций при подготовке студентов в строительном ВУЗе.
Разработка
проекта домов из бруса. Определить способы распила двух
партий бревен для получения максимального числа комплектов, состоящих из двух
брусьев длиной 2,2 м и одного длиной 1,3 м. Первая партия состоит из 99 бревен длиной 6,6 м, вторая - 60 бревен по
4,8 м.
Составим возможные способы распила, определим
значение ![]() , где i=1,2;
r=1,2 (табл.1).
, где i=1,2;
r=1,2 (табл.1).
Таблица 1.
Способы распила
|
Партия |
Размер брусьев |
j=1 |
j=2 |
j=3 |
j=4 |
f1 |
|
I (i=1) (6,6 м) |
2,2 м (r=1) 1,3 м (r=2) |
3 - |
2 1 |
1 3 |
- 5 |
f1 f2 |
|
II (i=2) (4,8 м) |
2,2 м (r=1) 1,3 м (r=2) |
2 - |
1 2 |
- 3 |
- - |
f1 f2 |
Обозначим через ![]() (i=1,2;
j=1,2,3,4) количество бревен в первой и второй
партиях, распиленных 1,…,4 способами, и составим математическую модель задачи.
(i=1,2;
j=1,2,3,4) количество бревен в первой и второй
партиях, распиленных 1,…,4 способами, и составим математическую модель задачи.
Выражение для целевой
функции определим из условия комплектности:
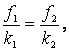
![]() ;
; 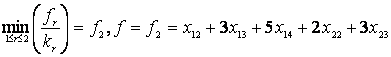 .
.
Ограничение
по комплектности получим из равенства ![]() :
:
![]()
или
![]()
С учетом ограничений по материальным
ресурсам, получим искомую математическую модель:
найти максимальное
значение линейной функции
![]()
при ограничениях
![]()
![]()
![]() ,
,
![]() - целые;
- целые; ![]()
Принимая
за базисные переменные ![]() , получим
, получим
![]()
при
ограничениях
![]() ,
, ![]()
![]()
![]() .
.
Далее примем за базисные переменные ![]() . Получили
искомый оптимальный план:
. Получили
искомый оптимальный план: ![]() (90 бревен по 6,6 м распилить на 3 части по
2,2 м; 9 бревен по 6,6 м - на 5 частей
по 1,3 м; 60 бревен по 4,8 м - на 5 частей по 1,3 м; 60 бревен по 4,8 м - на 3
части (один имеет длину 2,2 м; а два других -1,3 м)). При этом максимальное
количество комплектов
(90 бревен по 6,6 м распилить на 3 части по
2,2 м; 9 бревен по 6,6 м - на 5 частей
по 1,3 м; 60 бревен по 4,8 м - на 5 частей по 1,3 м; 60 бревен по 4,8 м - на 3
части (один имеет длину 2,2 м; а два других -1,3 м)). При этом максимальное
количество комплектов![]() .
.
Модульное
строительство. Пусть для строительства архитектурных
сооружений двух типов имеется 100 модулей. На строительство сооружений первого
типа расходуется 2 модуля, а на второй тип – 4 модуля. Составить план
производства, обеспечивающий получение наибольшей прибыли, если прибыль от
строительства сооружений первого типа составляет 300 тыс. рублей, а от строительства
второго типа – 200 тыс. рублей. Причем сооружений первого типа требуется не
более 40, а сооружений второго типа – не более 20.
Пусть ![]() - количество
сооружений первого и второго типа соответственно. Тогда
- количество
сооружений первого и второго типа соответственно. Тогда ![]() .
.
Выберем за базисные
переменные ![]() . Получим
. Получим
![]()
![]() .
.
Так что будем иметь ![]()
Первое допустимое решение ![]() ;
;![]() .
.
Увеличения ![]() можно достичь путем
увеличения
можно достичь путем
увеличения ![]() за счет увеличения
за счет увеличения ![]() . Но увеличивать
. Но увеличивать ![]() можно лишь до тех пор,
пока
можно лишь до тех пор,
пока ![]() или
или ![]() не обратятся в нуль (
не обратятся в нуль (![]() при увеличении
при увеличении ![]() в нуль не обратится).
Из
в нуль не обратится).
Из ![]() следует, что
следует, что ![]() при
при ![]() ;
; ![]() при
при ![]() ; то есть
; то есть ![]() можно увеличивать до
можно увеличивать до ![]() . При этом
. При этом ![]() . Получим второе допустимое решение
. Получим второе допустимое решение ![]() .
.
Введем в базис ![]() , исключив
, исключив ![]() . Имеем
. Имеем ![]() . Откуда
. Откуда ![]() . При этом
. При этом ![]() . Таким образом,
. Таким образом, ![]()
![]() ;
;
![]() . Коэффициент при
. Коэффициент при ![]() отрицателен. Увеличение
отрицателен. Увеличение
![]() лишь уменьшает
лишь уменьшает ![]() . Поэтому оптимальным
решением является
. Поэтому оптимальным
решением является ![]()
![]() ;
;![]() тыс.руб.
тыс.руб.
Методы решения приведенных задач связаны с именем
российского Лауреата Нобелевской премии по экономике Л.В.Канторовича (за вклад
в теорию оптимального распределения ресурсов; 1975 г.). Аналогичные задачи
возникают при проектировании строительных смесей, логистике (транспортная
задача), размещении сети культурно-бытового
обслуживания, распределении выпуска продукции по предприятиям, оптимальном использовании
оборудования и др. Практика показала, что изучение математического программирования
вызывает интерес у студентов и во многом способствует формированию их
компетенций для будущей профессиональной деятельности [4…6].
Литература
1. Данилов А.М., Гарькина И.А. Образовательная
система с позиций идентификации и управления / Региональная архитектура и
строительство. -2013. -№ 2.-
С. 143-146.
2.
Данилов А.М., Гарькина
И.А., Домке Э.Р. Математическое и компьютерное моделирование сложных систем
– Пенза: ПГУАС. –
2011.- 296 с.
3. Скачков Ю.П., Данилов А.М., Гарькина И.А.
Модификация
метода ПАТТЕРН к решению архитектурно-строительных задач / Региональная архитектура и
строительство. -2011. -№ 1.
-С. 4-9.
4. Гарькина И.А. Компетентностный
подход при подготовке специалистов с профессиональными качествами на примере
изучения дисциплины «Математика» / Образование и наука в
современном мире. Инновации. -2017. -№ 3 (10).
-С. 8-15.
5. Гарькина И.А., Стрельцова А.А. Математические
методы в практических задачах строительного профиля / Теория. Практика.
Инновации. -2017. -№ 4 (16).
-С. 16-19.
6. Гарькина И.А., Николотов В.Ю. Компетентностный
подход: задачи прикладной направленности при изучении математики / Теория. Практика.
Инновации. -2017.
-№ 5 (17).- С. 61-66.