УЧЕТ СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК
ПРИ ОПРЕДЕЛЕНИИ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
ЭРГАТИЧЕСКОЙ СИСТЕМЫ
Нашивочников В.В., Данилов А.М.
Пензенский государственный университет архитектуры и строительства
Классическим, традиционным
считается определение оценок передаточных функций по спектральным
характеристикам. Однако наблюдается сильное расхождение результатов в
зависимости от параметров дискретизации, длительности рассматриваемых реализаций
и применяемых для сглаживания (с неизбежными элементами субъективизма при их выборе)
различных типов окон [1…3]. Известно, что точность определения передаточных
характеристик вдали от доминирующих частот крайне низка. Правда, в этих зонах высокая
точность и не нужна: оператор управляет объектом на частотах, близких к его собственной частоте (связь
входного сигнала со спектральной характеристикой, рис.1).
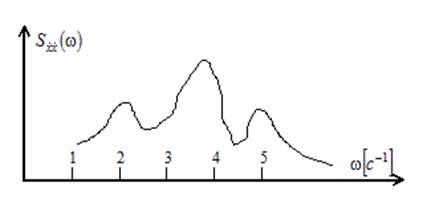
Рис.1. Энергетический спектр
Для некоторых режимов
функционирования зоны доминирующих частот (здесь возможна их линейная
аппроксимация) можно определить по обобщенным АЧХ и ФЧХ (решением уравнений
идентификации). В этих зонах оператор воспринимает объект как усилительное
звено с запаздыванием.
Идентификация
динамической системы в частотной области относится к классу некорректных задач
[4]. Так, для разомкнутой стационарной системы с одним входом и одним выходом
импульсная переходная функция определяется выражением
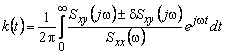 ,
,
а норма ошибки решения -
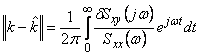 .
.
Как видим, ошибка может быть как
угодно велика в зависимости от распределения спектральной плотности входного
сигнала ![]() (если
(если ![]() и
и ![]() имеют нули одинаковой
кратности в какой-либо конечной точке оси
имеют нули одинаковой
кратности в какой-либо конечной точке оси ![]() , то погрешность решения может быть как угодно большой). Для рассматриваемого здесь класса эргатических систем рабочая
частотная область по каждому из каналов управления достаточно узка (0,7…7 с-1). Точность определения
частотных передаточных функций
, то погрешность решения может быть как угодно большой). Для рассматриваемого здесь класса эргатических систем рабочая
частотная область по каждому из каналов управления достаточно узка (0,7…7 с-1). Точность определения
частотных передаточных функций ![]() зависит от
спектральной плотности входного сигнала. Обычно оценка точности определения
зависит от
спектральной плотности входного сигнала. Обычно оценка точности определения ![]() на разных частотах
производится с весом, пропорциональным спектральной плотности
на разных частотах
производится с весом, пропорциональным спектральной плотности ![]() , в соответствии с
, в соответствии с ![]() -критерием:
-критерием:
 .
.
Вблизи каждой характерной
(резонансной) частоты входного сигнала возможна линейная аппроксимация
частотных характеристик (рис.3; согласуется с полученными по данным нормальной
эксплуатации обобщенными частотными характеристиками; по одному из каналов
резонансная частота – 5 с-1).
По синхронным измерениям ![]() ,
, ![]() ;
; ![]() в процессе нормальной эксплуатации эргатической системы
в процессе нормальной эксплуатации эргатической системы
![]() ,
, ![]() .
.
были получены элементы матрицы P.
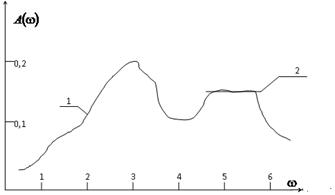
Рис.2. Обобщенные частотные характеристики:
кривая 1 – экспериментальная, 2 – аппроксимированная
В дискретной форме:
![]() ,
, ![]() .
.
Откуда
![]() ;
; ![]() ,
,
 ,
, 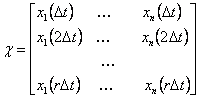 .
.
В случае, когда оператор можно
представить как инерционное звено второго порядка с запаздыванием, а для формирования управляющих воздействий
оператором используются как фазовые координаты, так и скорости и ускорения,
имеем:
![]()
![]() .
.
В дискретной форме:
![]() ;
; ![]() ,
,
![]() ;
; ![]() .
.
Тогда
![]() ;
;
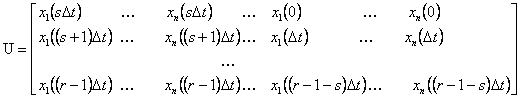 ,
,
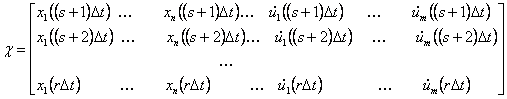 .
.
Сравнение параметров оптимальных
управлений на имитаторе и реальном объекте показало возможность получения
требуемых имитационных характеристик [5].
Литература
1.
Гарькина И.А.,
Данилов А.М., Домке Э.Р. Математическое
моделирование управляющих воздействий оператора в эргатической
системе / Вестник
Московского автомобильно-дорожного государственного технического университета
(МАДИ). - 2011. - № 2.
- С. 18-23.
2.
Будылина Е.А., Гарькина И.А., Данилов А.М. Приближенные методы декомпозиции при настройке имитаторов
динамических систем / Региональная архитектура и
строительство. - 2013. - № 3.
= С. 150-156.
3.
Гарькина И.А.,
Данилов А.М., Пылайкин С.А.Транспортные
эргатические системы: информационные модели и
управление / Мир транспорта и технологических
машин. -2013. -№ 1 (40).
-С. 113-120.
4.
Данилов А.М., Гарькина
И.А., Домке Э.Р. Математическое
и компьютерное моделирование сложных систем / Пенза: ПГУАС. 2011. - 296 с.
5.
Гарькина И.А.,
Данилов А.М., Пылайкин С.А. Тренажеры и
имитаторы транспортных систем: выбор параметров вычислений, оценка качества
/ Мир
транспорта и технологических машин. -2013. -№ 3 (42).
- С. 115-120.