СОВРЕМЕННЫЕ ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ/2.Вычислительная техника и программирование

Степова Т.О.

Вінницький національний технічний університет, Україна

Практична реалізація інтервального методу в оптичних дослідженнях

Сучасні дослідження складних систем різного призначення вимагають широкого використання математичних моделей, що враховують невизначеність, в умовах якої працює більшість систем. Незалежно від способу отримання таких моделей, усі вони є лише наближеним спрощеним описом системи, що досліджується, оскільки будуються в умовах невизначеності та неповноти інформації.

Останнім часом для моделювання складних систем в умовах невизначеності інтенсивно застосовуються методи інтервального аналізу, які вимагають мінімальної кількості інформації про досліджувану систему. В результаті застосування інтервальних методів замість одного значення на виході системи отримують множину рівнозначних величин, що містяться у вихідному інтервалі.

Разом з тим, раніше розроблені в рамках інтервального аналізу методи не забезпечують зростаючих потреб у математичному моделюванні складних систем. Тому розробка теоретичних засад побудови моделей складних систем на основі методів інтервального аналізу, що розглядається в цій роботі, є актуальною та важливою науковою задачею математичного моделювання.

Результати експериментів щодо вивчення розповсюдження світла в різних середовищах дозволили встановити існування двох станів світла: природного та поляризованого.

Фізіологічна дія поляризованого світла на сітківку ока нічим не відрізняється від дії природного світла. Тому для вивчення його властивостей необхідні пристрої для його одержання і дослідження.

Пристрій, що дає можливість одержувати поляризовані промені, називається поляризатором, а пристрій, що дозволяє виявити наявність поляризованого світла — аналізатором. Слід відмітити, що обидва ці пристрої взаємно заміняються.

Особливістю поляризатора і аналізатора є те, що вони можуть пропускати світлові хвилі, електричний вектор напруженості яких коливається лише в строго визначеному напрямі. Такий напрям називається головним.

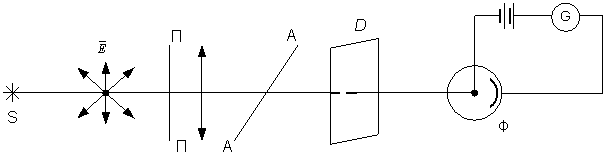Рисунок 1 – Експериментальна установка

Розглянемо установку (рис.1), що складається з джерела світла S, поляризатора П, аналізатора А, фотоелемента Ф, гальванометра G. Після проходження через поляризатор П світло стає плоскополяризованим. Аналізатор може пропускати тільки ті коливання , які збігаються з його головним напрямком АА. Якщо головні напрямки поляризатора ПП і аналізатора АА збігаються, то інтенсивність світла, що проходить через аналізатор А, буде максимальною.

Коли головні напрямки поляризатора і аналізатора утворюють між собою деякий кут φ, інтенсивність світла, що проходить, буде мати проміжне значення. Встановлений зв'язок між інтенсивністю променя, що проходить, і кутом φ можна визначити через співвідношення, що виражає закон Малюса:

I = I₀cos² φ (1)

Результати за формулою при значеннях кута на інтервалі та при відомому числі представлено на рис. 2. Але звісно, при проведенні реального експерименту, результати будуть різнитися, як це можна відмітити за рис. 3.

Як можна побачити, результати реального експерименту мають певні відхилення від обчислень за формулою (1), тому є необхідним оцінка точності експерименту. Для цього доцільним є застосування різних методів апроксимації функцій.

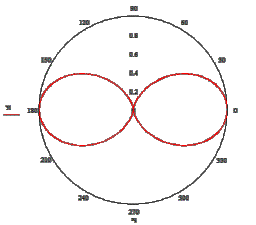
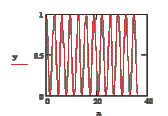
Рисунок 2 – Результати обчислень інтенсивності променя за законом Малюса

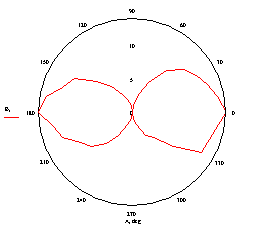
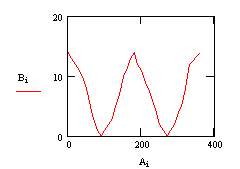
Рисунок 3 – Інтенсивність променя за результатами експерименту

В багатьох випадках, особливо при обробці експериментальних даних, середньоквадратичне наближення зручне, оскільки воно згладжує деякі неточності функції і дає достатньо правильне уявлення про неї. Однак, іноді ставиться більш жорстка умова і вимагається, щоб у всіх точках деякого відрізку [a, b] модуль відхилення многочлена φ(х) від f(х) був менший від деякого ε. В цьому випадку маємо рівномірну апроксимацію, при якій абсолютним відхиленням Δ многочлена φ(х) від функції f(х) на відрізку [a, b] називається максимальне значення абсолютної різниці між ними на даному відрізку: Δ = max | f(х) – φ(х)| , (2)

За аналогією можна ввести середньоквадратичне відхилення

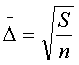(3)

При середньоквадратичному наближенні степінь полінома m, як правило, значно менша від n. На практиці не вище 5,6. Мірою відхилення многочлена φ(х) від заданої функції f(х) на множині точок (x_i, y_i) (і =) є величина S

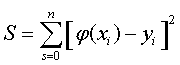(4)

При побудові апроксимуючого многочлена потрібно підібрати коефіцієнти а₀, а₁, … , а_m так, щоб величина S була мінімальна. В цьому полягає ідея методу найменших квадратів.

На рисунку 1 показано відмінність цих двох видів наближень.

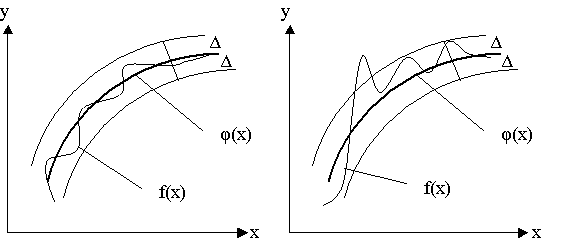Рівномірне середньоквадратичне

Рисунок 4 – Різні види наближень.

Таким чином, розкрита основна мета апроксимації – одержати швидкий (економний) алгоритм обчислення значень f(x) для значень x, що не містяться в таблиці даних. Представлена похибка та сума квадратів таких похибок при застосуванні процесу апроксимації для масивів з інтервальними даними.