Ст. преп. Дзогий И.В.
Брянский государственный университет имени ак. И.Г. Петровского,
Россия
Многомерные сингулярные интегральные
уравнения, связанные со сложными каноническими особенностями.
Пусть ![]() - пространство
интегрируемых с квадратом по Лебегу функций
- пространство
интегрируемых с квадратом по Лебегу функций ![]() .
.
Рассмотрим ![]() выпуклых острых
непересекающихся конусов
выпуклых острых
непересекающихся конусов ![]() в
в
![]() -мерном пространстве
-мерном пространстве ![]() . Обозначим
через
. Обозначим
через ![]() радиальную трубчатую
область, где
радиальную трубчатую
область, где
![]() (1)
(1)
сопряженный
конус к конусу ![]() ,
, ![]() (см. [7], [8]).
(см. [7], [8]).
Обозначим через ![]() подпространство из
подпространство из ![]() функций
функций ![]() , допускающих аналитическое продолжение в радиальную
трубчатую область
, допускающих аналитическое продолжение в радиальную
трубчатую область ![]() и удовлетворяющих
условию
и удовлетворяющих
условию
![]() . (2)
. (2)
Обозначим через ![]() пространство,
являющееся прямым дополнением к пространству
пространство,
являющееся прямым дополнением к пространству ![]() в
в ![]() , то есть выполняется равенство
, то есть выполняется равенство
![]() . (3)
. (3)
Определим
пространство функций ![]() из соотношения
из соотношения
 , (4)
, (4)
где 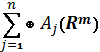 - прямая сума
пространств
- прямая сума
пространств ![]() ,
, ![]() .
.
Теорема 1(см. [9],
[10]). Каждому решению задач вида
![]() ,
, ![]() , (5)
, (5)
где ![]() ,
, ![]() , соответствует
решение задачи
, соответствует
решение задачи
![]() , (6)
, (6)
где 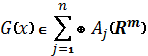 ,
, ![]() и
и
![]() ,
, ![]() . (7)
. (7)
Обратно,
каждое решение задачи (6) можно представить в виде (5).
Решить
какую-нибудь задачу из (5) можно при условии существования 0-волновой
факторизации функции ![]() относительно
соответствующего конуса
относительно
соответствующего конуса ![]() .
.
Пусть ![]() ограничен сверху и
снизу положительными константами.
ограничен сверху и
снизу положительными константами.
Определение (см. [5], [6]). 0-волновой
факторизацией функции ![]() относительно конуса
относительно конуса ![]() называется ее
представление в виде
называется ее
представление в виде
![]() , (8)
, (8)
где
функции ![]() ,
, ![]() допускают
ограниченное аналитическое продолжение в радиальные трубчатые области
допускают
ограниченное аналитическое продолжение в радиальные трубчатые области ![]() ,
, ![]() соответствено.
соответствено.
Теорема 2 (см. [9], [10]). Если функция ![]() ограничена сверху и
снизу положительными константами, и
ограничена сверху и
снизу положительными константами, и ![]() допускает 0-волновую факторизацию
относительно какого-нибудь конуса
допускает 0-волновую факторизацию
относительно какого-нибудь конуса ![]() , то задача () имеет
единственное решение.
, то задача () имеет
единственное решение.
Пусть
теперь в пространстве ![]() заданы
заданы ![]() выпуклых острых
непересекающихся конусов
выпуклых острых
непересекающихся конусов ![]() ,
, ![]() , таких, что
, таких, что
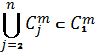 . (9)
. (9)
Обозначим через ![]() пространство функций
таких, что
пространство функций
таких, что
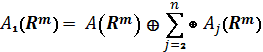 . (10)
. (10)
Тогда пространство ![]() будет иметь вид
будет иметь вид
 . (11)
. (11)
Теорема 3 (см. [9], [10]). Каждому решению задач
вида
![]() , (12)
, (12)
![]() ,
, ![]() , (13)
, (13)
где ![]() ,
, ![]() , соответствует
решение задачи
, соответствует
решение задачи
![]() , (14)
, (14)
где ![]() и
и
![]() ,
, 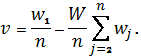 (15)
(15)
Обратно,
каждое решение задачи (14) можно записать в виде одной из задач (12), (13).
Литература
1. Гахов Ф.Д. Краевые задачи. / Ф.Д. Гахов. М.:
Наука, 1977. 640с.
2. Мусхелишвили Н.И. Сингулярные интегральные
уравнения. / Н.И. Мусхелишвили. М.: Наука,1968.
3. Голберг И.Ц., Крупник Н.Я. Введение в теорию
одномерных сингулярных интегральных операторов. / И.Ц. Голберг, Н.Я. Крупник. Кишинев: Штинца, 1973.
4. Вишик М.И., Эскин Г.И. Уравнения в свертках в
ограниченной области. / М.И. Вишик,
Г.И. Эскин. // Успехи математических наук. 1965. Т. 20, №3. С. 89-152.
5. Васильев В.Б. Регуляризация многомерных
сингулярных интегральных уравнений в негладких областях. / В.Б. Васильев //
Труды Московск. матем.о-ва. 1998. Т. 59. С.73-105.
6. Васильев В.Б. Волновая факторизация эллиптических
символов. / В.Б. Васильев // Математические заметки. 2000. Т. 69, №5. С.
653-667.
7. Владимиров В.С. Методы теорий функций многих
комплексных переменных. В.С. Владимиров. М.: Наука, 1964.
8. Бохнер С., Мартин У.Т. Функции многих
комплексных переменных. М.: ИИЛ, 1951. 300с.
9. Васильев В.Б., Щербенко И.В. Сингулярные
интегральные уравнения, связанные с многомерными сложными особенностями. / В.Б.
Васильев, И.В. Щербенко // Вестник Харьковского национального университета. -
Хорьков. - 2005. - Т. 4, № 661 - С.
61-68.
10. Васильев В.Б., Щербенко И.В. Многомерная
задача Римана для сложных особенностей. / В.Б. Васильев, И.В. Щербенко // Труды
XII международного симпозиума "Методы дискретных особенностей
в задачах математической физики". - Харьков-Херсон- 2005. - С. 59-62.