Листопадова В.В.

Національний технічний університет України «КПІ»

ПРУЖНА ДІЯ ЗВУКОВОЇ ХВИЛІ НА ПЛАСТИНУ. НЕСТАЦІОНАРНА ЗАДАЧА

При нестаціонарній пружній взаємодії, диференціальне рівняння збуреного згинного руху пластини матиме вигляд:

, (1)

де ; – час.

Праву частину рівняння задамо наступним чином

, (2)

де , причому обмеження на цей параметр уточнимо згодом.

Розв’язок рівняння (1) шукаємо у вигляді:

. (3)

Множник , який не залежить від часу, назвемо амплітудою коливань.

Підставимо (3) у вихідне рівняння (1):

, (4)

де .

Відшукуємо наближені розв’язки:

. (5)

Стовпець

(6)

підлягає визначенню.

Підстановка (5) в рівняння (4) приводить до наближеної рівності

, (7)

для якої стовпець (6) вважаємо за найбільш слушний у тому розумінні, що проекції лівої і правої частин виразу (7) на лінійну оболонку образів координатних функцій були би рівними.

Помножимо обидві частини рівності (7) на

.

Одержуємо:

. (8)

Матриця Грама образів координатних функцій

знайдена раніше. Стовпець також знайдений. Таким чином, залишається скласти матрицю

, (9)

яку назвемо матрицею Грама координатних функцій по енергії оператора . Після обчислення отримуємо –

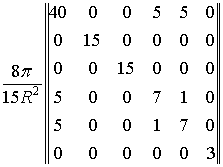. (10)

Знаючи матрицю Грама образів координатних функцій, а також матрицю Грама координатних функцій по енергії оператора (10), систему (8) можна навести інакше –

. (11)

Якщо , то ця система однозначно розв’язувана, тобто

, (12)

і можна будувати наближене розв’язання рівняння (4) у формі (5).

У зв’язку з тим, що матриця неособлива (невироджена), тому

,

де – одинична матриця. Отже,

;

.

Але є многочлен ступеня відносно . І якщо виявиться додатним коренем цього рівняння, тоді система (11) може стати нерозв’язуваною.