УДК 536.21;
539.3
Д. физ-мат наук, профессор
Геворкян Р.С., Асратян М.Г.
Институт
механики НАН РА
ОБ АСИМПТОТИЧЕСКОМ АНАЛИЗЕ РЕШЕНИЙ КОРРЕКТНЫХ
И
,,НЕКОРРЕКТНЫХ
ПО АДАМАРУ” ЗАДАЧ ДЛЯ ЭЛЛИПТИЧЕСКИХ
УРАВНЕНИЙ СТАЦИОНАРНОЙ ТЕПЛОПРОВОДНОСТИ И ТЕОРИИ
УПРУГОСТИ
Асимптотическим
методом решены классически корректные
задачи Дирихле и Неймана для эллиптических уравнений Пуассона (и Лапласа)
(гармоническoe уравнениe стационарной теплопроводности) и двумерные задачи
плоской деформации теории упругости (бигармоническoe уравнениe) со смешанными
статическими граничними условиями.
Используя те же самые общие интегралы и соответствующие рекурренные формулы для
указанных уранений решены ,,некорректные
по Адамару” задачи (краевые задачи, где
на одной границе области заданные условия перенасыщены, а на другой – вообще не заданы). Путем подходящего
пoдбора граничных условий (функций заданных на границах) классически корректной
задачи получены регулярные решения соответствующих ,,некорректных по Адамару” задач. Для рассмотренных краевых
задач выведенными решениями выявлена существующая взаимооднозначная связь между
классически корректными и
неклассическими граничными условиями с любой заранее выбранной
асимптотической точностью. Доказана, что
при заданных на продольных границах полосы (или пластины) бесконечных
размеров полиномиальных граничных условий, полученные решения краевых задач
математически точные, непрерывные и единственные. Выведены решения классически
корректных задач тождественно совпападающих с решениями соответствующих
,,некорректных по Адамару” задач.
В последние годы проявляется повышенный интерес к
краевым задачам математической физики, когда по какой нибудь причине на одной
части поверхности области занимаемой
материальным телом заданы граничные
условия больше чем необходимы для
краевой задачи данного класса, а на другой части – меньше чем необходимы
или вообще не заданы [1–5]. Такие
задачи называются “некорректными по Адамару” [6,7]. Их возникновение связано с,
практически, невозможностью (или ограниченной возможностью) произвести
измерения необходимых физических величин на этой части поверхности тела.
Учитывая
практиическую значимость решений “некорректных” задач и тот факт, что одним из
методов их решения считается приближенный метод [6–7], а
также
учитывая
эффективность асимптотического метода для решения краевых задач теории пластин и оболочек [2,5,9–11], где решения
представляются в виде полиномов по поперечным координатам, в предлагаемой
работе асимптотическим методом строятся общие интегралы в виде рекуррентных
формул для эллиптических уравнений второго порядка задачи стационарной
теплопроводности и четвертого порядка двумерной задачи плоской деформации
теории упругости со смешанными статическими граническими условиями. С помощью выведенных рекуррентных
формул, решаются классически корректные и ,,некорректные” краевые задачи
теплопроводности и теории упругости для полосы бесконечной длины с определенной
асимптотической точностью. Доказано, что при подходящим подборе граничных
условий (функций, заданных на продольных крах полосы) между решениями
классически корректных и
соответствующих ,,некорректныех” задач существует взаимооднозначная регулярная
связь с такой же асимптотической точностью, а когда функции, заданные на
продольных крах полосы полиномы степени 
, то после 
шагов итерации
получаются математически точные и тождественно совпадающие решения
соответствующих корректных и ,,некорректных” краевых задач.
1. Общий
интеграл асимптотического решения двумерного уравнения Пуассона. Рассмотрим двумерное уравнение Пуассона в
прямоугольной области-полосе (бесконечной длины) и ширины 2h плоскости 
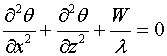(1.1)
В
частности, (1.1) может быть уравнение стационарной теплопроводности с заданной
удельной плотностью источника тепла 
B уравнении (1.1) перейдем к безразмерным
координатам по формулам
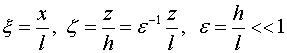(1.2)
получим
(1.3)
Уравнение
(1.3) сингулярно возмущена геометрическим малым параметром 
. Его
асимптотическое решение должно складываться из двух слагаемых: из
решения внутренней, основной задачи и согласованного с ним решения задачи в
пограничном слое вблизи торцов 
[9–12].
Решение внутренней задачи ищется в виде
асимптотического разложения
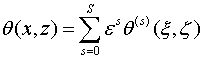(1.4)
одновременно, заданную в уравнении (1.1) функцию (в
частности, удельняя плотность источника тепла) представим в виде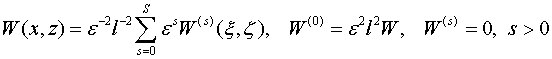 
(1.5)
Такое представление обеспечивает влияние функции 
на асимптотическое решение краевой задачи начиная с
первого шага итерационного процесса.
Подставив
(1.4),(1.5) в (1.3) и приравняв коэффициенты при 
в левой и
правой частях равенства получаем
разрешающее уравнение
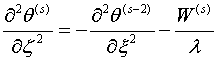(1.6)
общий интеграл которого имеет вид
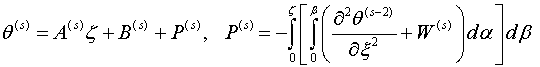(1.7)
где 
произвольные функции интегрирования.
Общее
решение (1.6) позволяет решить краевые задачи Дирихле и смещанные задачи (когда
на одном продольном крае задано значение функции, а на противоположном крае
значение ее нормальной производной (условие задачи Неймана) для бесконечной
полосы, поскольку найден общий интеграл только внутренней задачи.
2. Решения
(классически корректных) краевых задач.
а. Пусть
на продольных краях полосы заданы значения искомой функции (значения температур
для задачи стационарной теплопроводности)
(2.1)
Удовлетворив условиям (2.1) однозначно определяем функции интегрирования и
искомую функцию в виде рекуррентной формулы
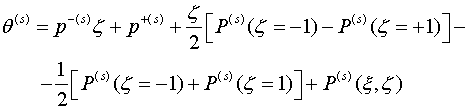(2.2)
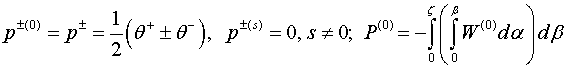
Вычислив пять
шагов итерации при 
, получаем
(2.3)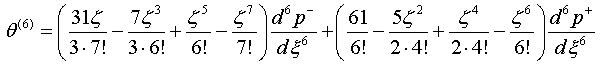 
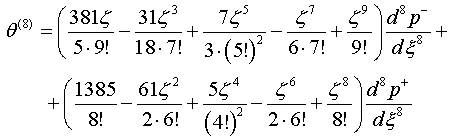
б. Пусть
на продольных краях полосы заданы смешанные условия: функция и ее нормальное
производное (значения температуры 
и плотности теплового потока
, задачи стационарной теплопроводности)
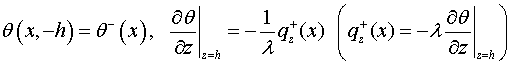(2.4)
тогда решение краевой задачи представляется
рекуррентной формулой
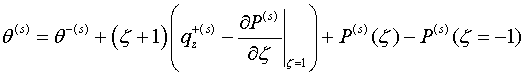(2.5)
Выпишем коэффициенты разложения (1.4) с точностью пяти
шагов итерации
при 
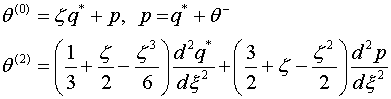
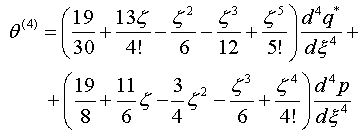
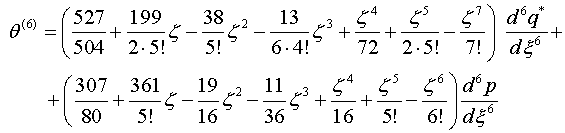(2.6)
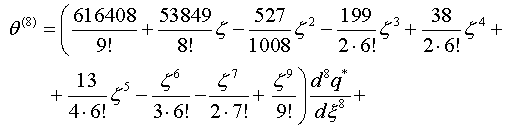
Следовательно после пяти шагов итерации
решениями краевых задач (1.1),(2.1) и (1.1),(2.2) при 
будут
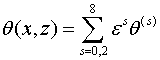(2.7)
когда 
определяются по
формулам (2.3) и (2.6) соответственно.
Асимптотическая точностью пяти шагов итерации
составляет 
, если заданные на краях полосы функции вместе со
своими производными непрерывные, ограниченные и имеют изменяемости порядка 
[11,12].
Заметим, что когда заданные в граничных условиях (2.1),(2.4) и в уравнении
(1.1) функции являются многочленами, то после конечного числа шагов
итерационный процесс обрывается и полуючаются математически точные (замкнутые)
решения поставленных краевых задач.
Учитывая,
что общий интеграл асимптотического решения, выраженный в виде рекуррентной
формулы (1.7), при заданных полиномиальных функциях приводит к точному
математическому решению краевой задачи, целесообразно решить также
,,некорректную по Адамару’’ задачу и выявить ее связь с приведенными выше
решениями классически корректных задач.
3. Решение
«некорректной» краевой задачи (стационарной
теплопроводности). Пусть на продольном крае 
полосы
заданы и температура, и тепловой поток,
а на потивоположном крае условия не заданы
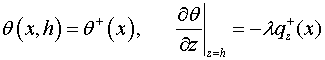(3.1)
тогда решение неклассической краевой задачи
представляется рекуррентной формулой
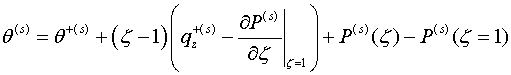(3.2)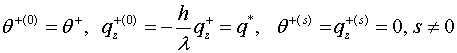 
Выпишем коэффициенты разложения (1.4) при
учете (3.1),(3.2) и 
с точностью
пяти шагов итерации
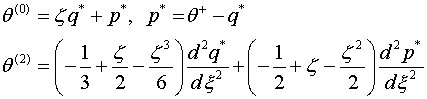
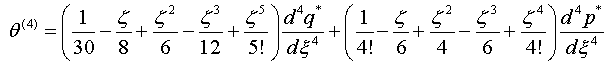
(3.3)
Заметим, что решение (3.3) с «некорректными»
граничными условиями (3.1) регулярное, имеет асимптотическую точность 
, когда функции (3.1)
заданные на продольном крае 
полосы
непрерывные, ограниченные и имеют такие же производные необходимого порядка с изменяемостью порядка
. Заметим, что решение (3.3) при учете (1.4)
«некорректной» задачи как и решения
(2.3),(2.6) классически корректных задач имеет асимптотическую точность пяти
шагов итерации – 
, а при полиномиальных (в данном случае не выше седьмой
степени) граничных условиях, оно математически точно удовлетворяет и уравнению
(1.6) при 
, и граничным условиям (3.1).
Учитывая это целесообразно установить: существует ли
связь между приведенными выше классически корректной и «некорректной» задачами?
Какая должна быть заданная на продольном крае 
функция
, чтобы решения (2.3),(2.7) и (2.6),(2.7) задач с
классически корректными граничными условиями соответственно (2.1) и (2.4)
удовлетворили также граничным условиям «некорректной» задачи (3.1) на
продольном крае 
?
Покажем, что
решение «некорректной» задачи (3.1)- (3.3),(2.7) можно получить из
решений каждой из классически корректных краевых задач (2.1)-(2.3),(2.7) и
(2.4)-(2.7) при подходящем выборе значении
функции 
, заданной на границе 
.
Из решения (3.1)-(3.3),(2.7) «некорректной» задачи вычислимлим
значение температурной функции 
( calculated) на продольном крае полосы 
:
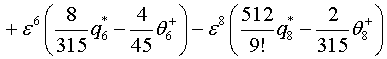(3.4)
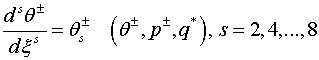
из решения корректной краевой задачи (2.1)-(2.3),(2.7)
значение 
на продольном
крае полосы 
:
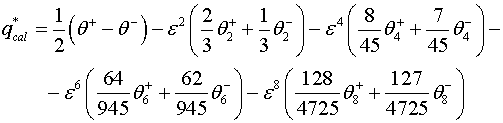(3.5)
подставив (3.4) в (3.5) получаем
(3.6)
что свидетельствует о том, что решение
(3.1)-(3.3),(2.7) «некорректной» задачи с асимптотической точностью 
совпадает с решением корректной краевой задачи
(2.1)-(2.3),(2.7), если 
. (Здесь учтено
то остоятельство, что сами решения краевых задач имеют асимптотическую точность
).
Аналогичным образом,
из решения (2.4)-(2.7) определим 
на границе 
:
(3.7)
куда подставив
(3.4), получим
(3.8)
Таким образом, с асимптотической точностью 
решения всех
приведенных выше трех краевых задач (с
классически коорректными и некорректными граничными условиями) совпадают, если
на границе 
принять 
. Эти решения совпадут тождественно (математически
точно), если заданные функции (2.1),(2.4),(3.1) многочлены не более восьмой
степени.
Приведем
пример: пусть на продольном крае 
полосы
заданы и температура, и тепловой поток
в виде квадратных трехчленов
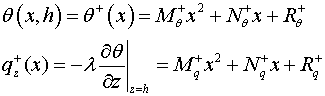(3.9)
а на потивоположном крае условия не заданы. После двух ходов итерации при учете
(3.1)-(3.2) и 
, решение такой “некорректной по Адамару”
(неклассической) краевой задачи, будет
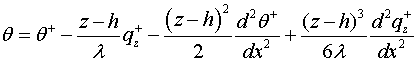(3.10)
Из
(3.1)-3.3),(3.9) следует, что (3.10) не содержит особенности. Оно математически
точное (замкнутое), поскольку
(3.11)
Для того, чтобы доказать идентичность решения (3.10) с
решением классической краевой задачи
стационарной теплопроводности, вычислим значение температуры полосы
на ее продольном крае 
согласно
неклассической задачи (3.9),(3.10). Оно
имеют вид
(3.12)
Рассмотрим полосу с классическими
граничными условиями первой краевой задачи теории нестационарной
теплопроводности (задача Дирихле)
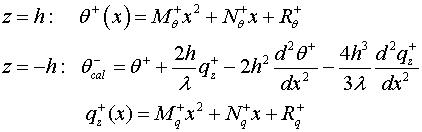(3.13)
После двух ходов итерации температурная функция
вычисленная по формулам (2.1)-(2.3) будет
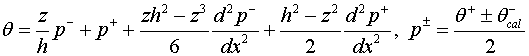(3.14)
Подставив значения велиличин из (3.13) в (3.14)
получим решение (3.10), что свидетельствует о идентичности решений (3.10) и (3.13).
4. Анализ асимптотических решений классически
корректной и
,,некорректной по Адамару” статических
краевых задач плоской деформации теории упругости. Выведем рекуррентные формулы общего решения уравнений
задачи плоской деформации теории
упругости в прямоугольной области – полосе 
.
Исходя
из уравнений и соотношений
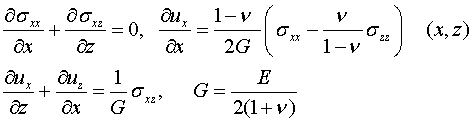(4.1)
следуя
[10], получаем
, 
, 
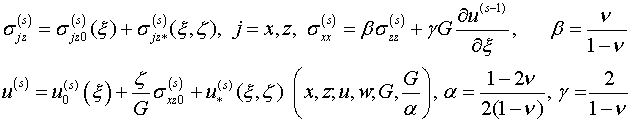
(4.2)
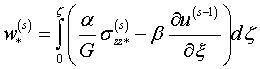
где четыре функций интегрирования 
,
которые
должны определиться из граничных условий, заданных на продольных краях 
и 
a. При смешанных граничных
условиях классически корректной задачи
(4.3)
функции
интегрирования будут
(4.4)
А
решение соответствующей классически корректной краевой задачи определяется
рекуррентными формулами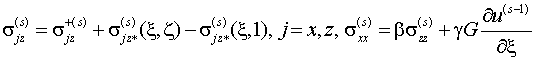 
(4.5)
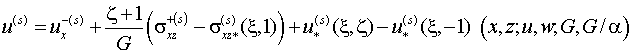
Приведем компоненты тензора напряжений и
вектора перемещения первых четырех шагов итерации
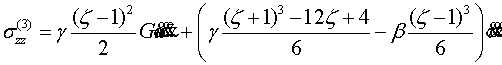
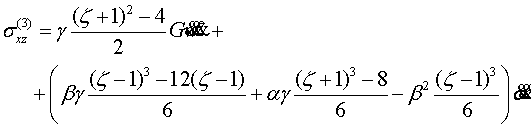
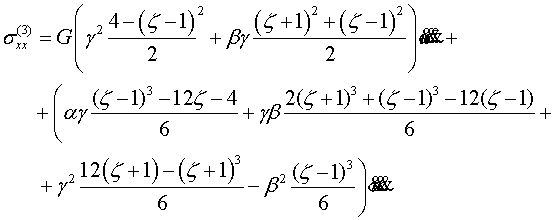(4.6)
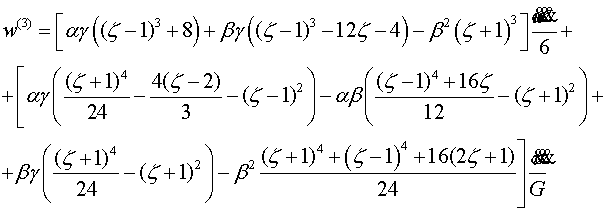
б. Выпишем решение ,,некорректной по Адамару” для полосы бесконечной
длины, когда только на одном продольном
крае 
заданы
неклассические условия краевой задачи
теории упругости
(4.7)
условия на торцевых сечениях 
не ставятся,
поскольку решается внутренная задача (в частности, для 
).
Удовлетворив граничным условиям (4.7) определяем функции интегрирования
(4.8)
Следовательно
решение ,,некорректной по Адамару” задачи
представляется рекуррентными формулами
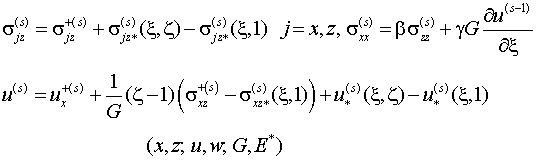(4.9)
Приведем компоненты тензора напряжений
и вектора перемещения первых четырех шагов итерации
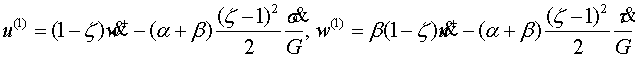
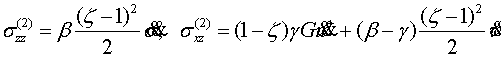
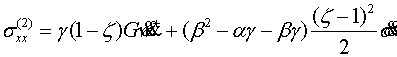
(4.10)
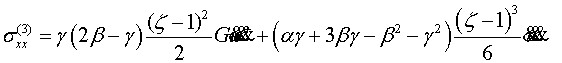
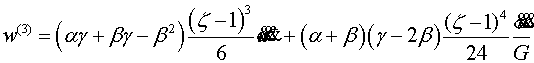
Таким
образом компоненты тензоров напряжений и векторов перемещений изотропной полосы
в классической и неклассической краевых задачах определяются суммами
, 
, 
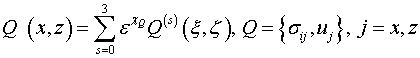(4.11)
с
учетом значений 
соответственно
для решений (4.6) – классической и (4.10) – неклассической краевых задач.
Заметим,
что краевые задачаи ,,а” и ,,б” вместе с решениами (4.6),(4.10) ,(4.11) корректные (в смысле:
решения существуют, единственные и регулярные), если заданные на границах функциях 
непрерывные,
ограниченные и имеют непрерывные и ограниченные производные требуемого порядка
(с изменяемостью 
[12,13]). А когда эти функции являются многочленами,
то после конечного числа шагов итерации обрываются и получаются замкнутые решения соответственно классической и
неклассической краевых задач для бесконечной полосы. Учитывая это,
целесообразно поставить дополнительную задачу: какими должны быть в
классической задаче заданные на продольном крае 
функции
перемещений 
, чтобы решение (4.6) на противоположном продольном
крае 
удовлетворило
также условиям ,,некорректной по
Адамару” задачи (4.7) ?
Для
этого вычислим перемещения
( calculated, classical) классической задачи, на линии 
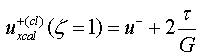
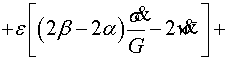
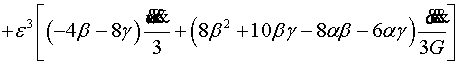(4.12)
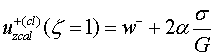
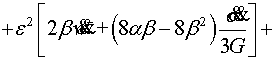
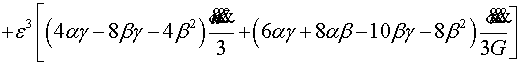
и неклассической 
( calculated, nonclassical) задачи, на линии 
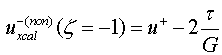
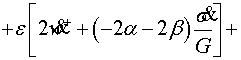
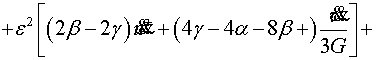
(4.13)
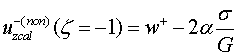
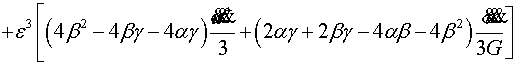
Подставив (4.13) в (4.12) находим связь меду
соответственно касательными и
нормальными перемещяниями на линии 
классической и
неклассической краевых задач.
(4.14)
Аналогичным образом, подставив (4.12) в (4.13) находим связь меду соответственно касательными и нормальными перемещяниями на
линии 
неклассической
и классической краевых задач.
(4.15)
Таким
образом решение (4.10) краевой задачи “б”
с неклассическими кревыми условиями
(4.7) из себя представляет определенная задача статической теории
упругости плоской деформации для полосы
бесконечной длины с классическими граничными условиями вида (4.3), точнее
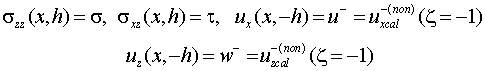(4.16)
где заданные перемещения 
определяются по
формулам (4.13).
Таким образом доказаны,что приведенные асимптотические решения ,,некорректных по
Адамару” задач эллиптических уравнений соответственно стационарной
теплопроводности и теории упругости из
себя представляют решения определенных корректных краевых задач с классическими
граничными условиями. Асимптотическая точность решения каждой задачи зависит от
количества шагов итерации и составляет
, если заданные функции непрерывные ограниченные и
имеют такие же производные требуемого порядка (с изменяемостью 
[11,12]). A если они полиномы степени 
то после 
шагов итерации,
она приводит к математически точным решениям краевых задач в многочленах
Учитывая это, считаем целесообразным, прежде чем удовлетворить неклассические граничные условия, измерения
физических величин, произведенные на одной и той же части поверхности
тела, интерполировать алгебраическими
многочленами (целыми функциями) степени 
В этом случае после 
шагов итерации получим математически точное
аналитическое решение краевой задачи в многочленах.
Приведем
пример: пусть имеем ,,некорректную” задачу теории
упругости полосы с неклассическими граничными условиями
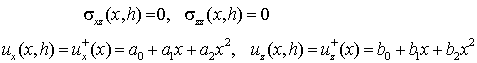(4.17)
Напряженно-деформированное
состояние полосы определяется формулами
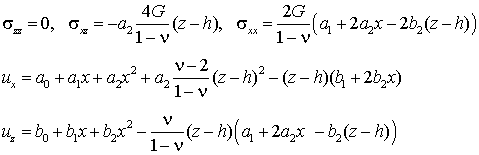(4.18)
Напряженно-деформированное
состояние полосы с классически корректными граничными условиями
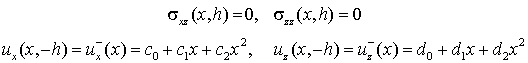(4.19)
определяется формулами
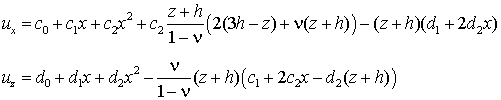(4.20)
(Решения (4.18) и (4.20) математически
точные – замкнутые).
Напряженно-деформированные
состояния (4.18) и (4.20) идентичны
(тождественно совпадают), если в (4.20) подставить
(4.21)
или в (4.18) подставить
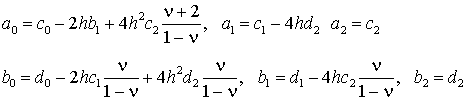(4.22)
Связь (4.21), (4.22) взаимооднозначна и
не содержит особенности, следовательно решение (4.18) ,,некорректной по
Адамару” задачи (4.17) является решением
конкретной классически
корректной зададачи (4.19). Оно существует единственное и регулярное.
Отметим,
что все рассуждения и выводы приведенные выше для задач стационарной
теплопроводности и теории упругости остаются в силе для соответствуюших
трехмерных краевых задач слоя (пластины бесконечных продольных размеров). А
выведенные выше рекуррентные формулы являются готовыми алгоритмами для
современной вычислительной техники,
позволяющей за считанные минуты вычислить сотни шагов итерации.
В заключении отметим важную область
практического применения решений задач теории упругости для слоя с
неклассическими граничными условиями в геофизике и сейсмологии. Известно, что
кора Земли состоит из литосферных плит, размеры которых составляют от сотен до
несколько тысяч квадратных киломеров. Они медленно перемещаются относительно
друг-друга, вследствие чего в зоне их
коллизии возникают мощные физические
поля, в частности, поля напряжений, деформаций а также тепловые поля.
Вследствии всего этого спутниковая система GPS регистртирует перемешения точек
поверхности земли на несколько сантиметров в год [2,13–16].
Используя данные GPS некоторого региона можно определить изменение напряженно-деформированного
состояния в данной зоне коллизии за определенный промежуток времени и
исползовать в прогнозах землетрясений, если эти изменения ближе к критическим.
Литература
1. Арутюнян
А.Г., Тоноян В.С., Хачикян А.С. Распределение деформаций в зоне взаимодействия
Аравийской и Евразиатской плит на основе данных GPS/ Изв.НАН Армении. Механика. 2003. Т.56. №3. С.3-13.
2. Aghalovyan L.A., Gevorgyan R.S., Sahakyan
A.V. Mathematical simulation of collision of arabian and euroasian plates on
the base of GPS data // Изв.НАН Армении. Механика. 2005. Т.58. №4. С.3-9.
3. Хачикян А.С. О гармонических и бигармонических
задачах для уравнений с неклассическими граничными условиями.// Изв.НАН
Армении. Механика. 2006. Т.59. №4. С.24-31.
4.
Саргсян В.Г., Хачикян А.С. О решении ,,некорректной ” задачи теплопроводности с
переопределенными исходными данными.// Изв.НАН Армении. Механика. 2008. Т.61.
№3. С. 58-63.
5.
Геворкян Р.С. Об асимптотическом
анализе решений корректных и «некорректных по Адамару» задач для эллиптических
уравнений математической физики (теплопроеодности) // Труды II международ.
конференции: Актуальные проблемы механики сплошной среды. Ереван: 2010.Том I.
С.182-186.
6. Лаврентьев М.М., Романов В.Г., Шишатский С.П.
Некорректные задачи математической физики и анализа. М.: „Наука", 1980.
286 с.
7.Тихонов А.Н., Арсенин В.Я. Методы решения
некорректных задач. М.: Наука, 1979. 286с.
9.Агаловян
Л. А. О структуре решения одного класса
плоских задач теории
упругости анизотропного тела// Меж вуз.
сборник н. трудов. Механика. Ереван: Изд-во ЕГУ, 1982. C. 7-12.
10.
Агаловян Л.А., Геворкян Р.С. Неклассические краевые задачи анизотропных
слоистых балок, пластин и оболочек. Ереван: Изд-во „Гитутюн" НАН РА, 2005.
468 с.
11.
Агаловян Л.А., Геворкян Р.С. Смешанные краевые задачи теории
упругости слоистых тонких тел
переменной толщины, состоящих из анизотропных неоднородных материалов// ПММ АН
РФ . 2009. Том. 73. Вып. 5. С.868-876.
12.
Гольденвейзер А.Л. Теория упругих тонких оболочек. М.: Наука,1976.512 с.
13 Aghalovyan L.A.
On one class of three-dimensional problems of elasticity thory for
plates //Proceedings of A. Razmadze Mathematikal Institute of Georgia. 2011. Vol.155, pp 3-10.
14. Академик Агаловян Л.А., Геворкян Р. С.,
Гулгазарян Л.Г. К определению напряженно-деформированных состояний
литосферных плит Земли на основе данных
GPS систем //Доклады НАН РА. 2012.
Том 112. №3. С.264-270
15.Aghalovyan L.A.
The Research of Lithospheric Plates
Tectonics of the Earth on the Base of
Data of Seismostations, GPS Sistems, the Solutions of problems of Elasticity Theory and the Earthquakes
Prediction. Proceedings of the15 th World Conference on Earthquake Engineering
(Lisbon, Portugal. 24-28
September, 2012). 15 WCEE – title index.WCEE 2012-3008.pdf.
16.Агаловян Л.А., Агаловян М.Л. О динамическом поведении литосферных плит Земли на
основе данных сейсмостанций и GPS
систем. Тр. Международной конф. “Актуальные проблемы механики сплошной
среды” (08-12 сентября 2012. Цахкадзор,
Армения). Ереван 2012.Т.1. С.42-46.