Сулейменов З.И. к.ф.-м.н., доцент,

Шанбаева Д.А. – магистр

Казахский Национальный технический университет имени К.И.Сатпаева

Стохастическое моделирование процесса миграции

солей в почвогрунтах

Влага существует в почве в результате естественного испарения из поверхности грунтовых вод, инфильтрации (дождь, снег), искусственного орошения, транспирации и т.п., и образует естественный почвенный раствор, в котором содержит определенное количество растворенных солей, причем концентрация раствора чрезвычайно изменчива и зависит от степени влажности грунта. При уменьшении влажности почвы часть растворенных солей может выпасть в кристаллы (твердую фазу), и, наоборот – при дополнительном поступлении влаги какая – то часть легкорастворимых солей может перейти обратно в раствор, изменяя его химический состав и общую минерализацию. Сами растворы суть электролиты, полученные в результате распада (диссоциации) в воде молекул кислот, солей и основании на ионы. В этой связи процесс миграции солей в однородных почвогрунтах рассматривается как движения ионов диссоцированных в воде молекул солей. Если представить пористую среду как совокупность большого числа взаимосвязанных пор, отличных один от другого, то каждый возможный путь движения ионов через пористую среду происходит с непрерывно меняющейся скоростью по системе взаимосвязанных пор. При этом в окрестности рассматриваемой точки некоторого объема проходят многие частицы жидкости с соответствующими скоростями (или элементарными вытеснениями). При стохастическом моделировании описанного процесса истинное значение скорости конкретной частицы в некоторой точке заменяется большим количеством возможных скоростей безымянных частиц [1, 2].

В данной работе рассмотрим стохастическую модель процесса миграции солей в почвогрунтах для одномерного случая, которая представляется как одномерная случайная траектория.

Пусть молекула (или ион) соли, участвующая в броуновском движении, в момент времени находится в точке 0 (рис.1). В данной модели эта молекула, в результате взаимодействия с соседними частицами, выполняет вытеснения по прямой линии в виде ряда шагов равной длины (рис. 1).

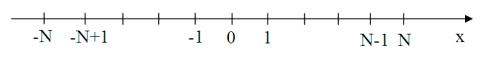
Рис. 1

Каждый шаг берется в двух противоположных направлениях с равной вероятностью 0,5. После прохождения таких отрезков молекула может находиться в любой из следующих точек:

Предположим, что каждый отрезок может быть взят одинаковым образом в любых направлениях независимо от всех предшествующих вытеснении. Тогда вероятность нахождения молекулы в любой последовательности отрезков равна (0,5)ⁿ.

Чтобы оказаться в точке после шагов, необходимо, чтобы отрезков брались в положительном, а остальные брались в отрицательном направлении. Общее число подобных последовательностей равно:

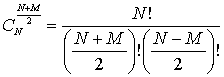. (1)

Тогда, вероятность того, что частица появится в точке после вытеснении, согласно распределению Бернулли, имеет вид:

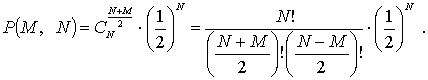(2)

Воспользовавшись формулой Стирлинга

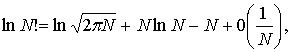(3)

получим

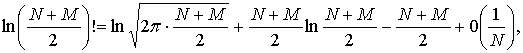(4)

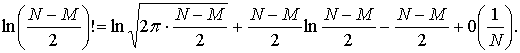(5)

Логарифмы в (4) и (5) при помощи формулы

запишем в виде

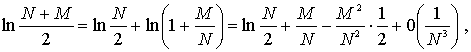(6)

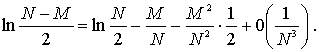(7)

Подставляя (3)-(7) в (2), при и , получим:

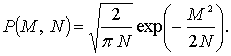(8)

Пусть , где - длина каждого отрезка. Вероятность того, что частица находится в интервале после вытеснений при , есть

или

. (9)

Если частица испытывает вытеснений в единицу времени, то вероятность того, что она находится на расстоянии в момент времени дается следующей формулой нормального распределения:

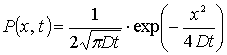, (10)

где .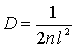

Если частица соли в момент времени находится в точке , то формула (10) имеет следующий вид:

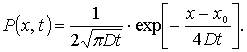(11)

Полученные плотности вероятностей (10), (11) дают распределения вероятностей по всем точкам прямой.

Плотность распределения вероятностей молекулы, находящейся в броуновском движении, отстоять на расстоянии от отталкивающей стенки полупрямой в момент , если в момент она отстояла на расстоянии , дается формулой [3]:

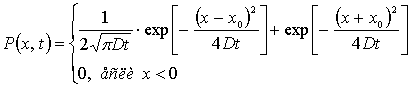, если

Математическое ожидание и дисперсия случайной величины распределенной по закону (10) равны соответственно:

В случае закона распределения (11), соответствующие величины получены:

Математическое ожидание случайной величины перемещения молекулы за время от до , плотность распределения которого дается формулой (12), получим согласно определению:

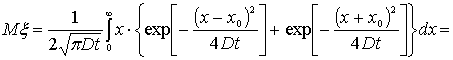
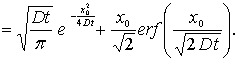
Где

Литература

1. Я.Бэр, Д.Заславски, С.Ирмей. Физико-математическое основы фильтрации воды. – Москва: Мир, 1971. – 451с.

2. Н.Н.Веригин, С.В.Васильев, Н.П.Куранов, В.С.Саркисян, Д.Ф.Шульгин. Методы прогноза солевого режима грунтов и грунтовых вод. – М.: Колос, 1979. – 336с. с ил.

3. Б.В. Гнеденко. Курс теории вероятностей. М.: Наука, 1988. – 448с.