Д.п.н. Хамов Г.Г., к.п.н. Тимофеева Л.Н.

Российский государственный педагогический университет им. А.И. Герцена,

Военно-космическая академия им. А Ф. Можайского, Россия

Исследовательские задания как средство активизации самостоятельной познавательной деятельности будущих учителей математики

В соответствии с федеральным государственным образовательным стандартом высшего профессионального образования организация процесса обучения в высшей школе направлена на обеспечение условий для непрерывного формирования профессиональной компетентности будущего специалиста. В связи с этим, в процессе подготовки будущего учителя необходимо сформировать содержание и педагогические условия для развития средств и методов обучения, способствующих: активизации самостоятельной познавательной деятельности студентов; овладению методами познания; повышению мотивации к самообразованию; творческому использованию полученных знаний [1]–[3]. Одним из путей такой организации учебного процесса на математических факультетах является вовлечение студентов в систематическую исследовательскую деятельность в процессе освоения математических дисциплин, при этом эффективность полученного результата зависит от подбора учебного материала, задач, примеров исследовательского характера как для аудиторной, так и для самостоятельной работы.

Приведем примеры заданий исследовательского характера по теме «Теория делимости в кольце целых чисел».

Задание 1. Найдите трехзначное число, представляющее собой три последовательные цифры, такие, что перестановка местами первых двух цифр дает число, являющееся полным квадратом.

Искомое число . Тогда . Из полученного равенства следует, что делится на 3. Искомое число 234 ().

Задание 2. Найдите наименьшее натуральное число оканчивающееся цифрой 7, перестановка которой из конца числа в его начало даст число в 5 раз большее данного.

Обозначив искомое число , составляем уравнение . Отсюда следует, что надо найти наименьшее натуральное число , при котором число при делении на 7 дает остаток 5, что возможно при , .

Задание 3. Докажите, что куб целого числа и куб его остатка от деления на некоторое натуральное число дают равные остатки при делении на то же число. Обобщите это свойство на любую натуральную степень.

По теореме о делении с остатком , . Далее возводим в куб (или другую натуральную степень) обе части полученного равенства.

Задание 4. Найдите возможные остатки от деления куба целого числа на 9.

Используя задание 3, находим возможные остатки: .

Задание 5. Четырехзначное число равно кубу суммы его цифр. Найдите это число.

Искомое число . Получаем уравнение .

Отсюда, так как куб целого числа при делении на 9 может давать остатки , то число при делении на 9 может давать эти же остатки. Кроме того, число будет четырехзначным, если , поэтому возможные значения для .

Искомые числа: .

Задание 6. Найдите двухзначное число, которое равно сумме квадрата числа его десятков и куба числа его единиц.

Имеем уравнение

Правая часть последнего уравнения число четное, поэтому и , при этом . Два числа 43, 63 удовлетворяют условию задачи.

Задание 7. Найдите четырехзначные числа, которые будучи приписаны справа к числу 900 дают полный квадрат.

Обозначая – искомое число, получаем уравнение .

Так как – натуральное число, то . Если , то – искомое число: . Других решений нет, так как при , – не четырехзначное число.

Задание 8. Найдите возможные остатки от деления квадрата целого числа на 7. Возможные остатки: 0;1;2;4.

Задание 9. При каких целых числах число вида является полным квадратом?

Задача сводится к решению неопределенного уравнения . Так как число – 2015 при делении на 7 дает остаток 1, то данному уравнению будет удовлетворять те числа , которые при делении на 7 дают остатки 1;6, т.е. число имеет вид . Подставляя в уравнение, находим множество решений

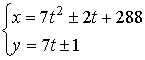, - целое, знак в формулах одинаков.

Заметим, что уравнения, содержащие две и более переменные и решаемые в целых числах, называют неопределенными (или диофантовыми). Задание 9 демонстрирует метод решения уравнений исследованием возможных остатков от деления обеих частей на одно и то же число.

Задание 10. Может ли число быть квадратом или кубом целого числа?

Составляем уравнения: , .

Далее исследуются возможные остатки от деления левой и правой частей первого уравнения на 5, второго на 13. Целых решений уравнения не имеют.

Задание 11. Докажите, что произведение двух целых чисел и произведение их остатков от деления на одно и то же число, дают равные остатки при делении на то же число.

Для перемножаемых чисел используется формула, вытекающая из теоремы о делении с остатком и выражающая данное число через делитель, делимое, частное и остаток.

Задание 12. Найдите все целые числа вида делящиеся на 7.

Задача сводится к нахождению целых чисел , удовлетворяющих уравнению .

Так как число 2015 при делении на 7 дает остаток 6, то находим значения , при которых дает остаток 6: , -целое.

Из уравнения находим: , -целое число, знак в формулах для и одинаков.

Задание 13. Составьте неопределенные уравнения второй степени, решаемые методом исследования остатков от деления на число 11 и содержащие заранее выбранное число, например, 2015.

Процесс составления такого вида уравнений основан на формуле, вытекающей из теоремы о делении с остатком: (1), где – делимое, – делитель, – частное, – остаток.

Производим в формуле (1) замену: вместо берем (или , – конкретное число); - делитель (например, 11); вместо – переменную (или для неразрешимых в целых числах уравнений); заменяется числом (например, 2015).

Примеры:

· , , . Решений нет.

· , множество решений: ,

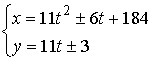· , решения: ,

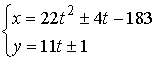· , решения: ,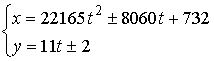

во всех ответах - целое число, знак в формулах одинаков.

Задание 14. Решите в целых числах уравнения:

ü .

Из уравнения следует, что целочисленные решения могут быть, если , , тогда . Полученное уравнение решается методом исследования остатков от деления на 7. Множество решений: 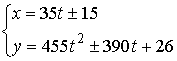, - целое число, знак в формулах одинаков.

ü . Решений нет.

ü . Решения: , .

ü .

Из уравнения: – четное. Тогда

Так как НОД, то делится на , что возможно при . Решения: (0; 0), (2; 1).

ü .

Решения: 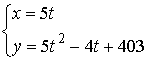, , 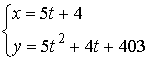– целое.

ü .

Исследовать остатки от деления на 8. Решений нет.

ü , = 2, 3, 4, 6, 7, 9, 10, 11.

Исследовать остатки от деления на 13. Решений нет.

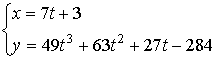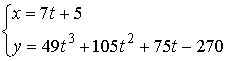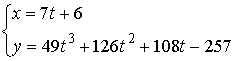ü . Множество решений: ; ; , - целое.

Значимость рассмотренного материала для будущего учителя математики обусловлена также его тесной связью со школьным курсом математики и программой углубленного изучения математики.

Литература:

1. Деза Е.И. Теория и практика фундаментальной подготовки учителя математики в условиях реализации индивидуальных образовательных траекторий. //Преподаватель XXI век. М., 2012, №2, с. 45-58.

2. Смирнов Е.И., Белкина В.Н., Тихомиров А.С., Трошина Т.Л. Фундирование в определении содержания математического образования будущего учителя. //Ярославский педагогический вестник. Научный журнал. Ярославль: Изд-во ЯГПУ им. К.Д. Ушинского, 2013. Том II. Психолого-педагогические науки, №3, с. 134-140.

3. Хамов Г.Г., Тимофеева Л.Н. Формирование исследовательских компетенций будущих учителей математики при изучении теоретико-числового материала. //Ярославский педагогический вестник. Научный журнал. Ярославль: Изд-во ЯГПУ им. К.Д. Ушинского, 2013. Том II. Психолого-педагогические науки, №3, с. 141-146.