СЛОЖНАЯ ДОМЕННАЯ СТРУКТУРА В МАГНИТНОЙ ПЛЕНКЕ С НАКЛОННОЙ АНИЗОТРОПИЕЙ

 

М. Л. Акимов, П. А. Поляков, Н. Н. Усманов

 

Московский государственный университет им. М. В .Ломоносова, Физический факультет, Россия

Хорошо известно, что в ферромагнитных пленочных материалах энергетически выгодно возникновение магнитного доменного упорядочения [1-2]. Равновесная доменная структура определяется балансом многих факторов, важнейшими из которых являются: обменное взаимодействие, анизотропия, магнитострикция, величина намагниченности, энергия доменных границ, форма магнитного образца, особенности структуры поверхности, величина и направление внешнего магнитного поля, температура, наличие дефектов. В магнитном образце в равновесном состояниии возникает вполне определенный тип магнитных доменов. Например, наиболее типичным видом магнитного упорядочения в магнитных пленках с перпендикулярной анизотропией является полосовая или лабиринтная доменная структура или решетка цилиндрических магнитных доменов [3].

В работах [4, 5] экспериментально и теоретически показана возможность реализации и существования квазиравновесной смешанной доменной структуры, представляющей собой систему полосовых доменов и цилиндрического магнитного домена, причем эта структура устойчива и может существовать бесконечно долго. Для реализации рассчитанной конфигурации в эксперименте использовалась пленка состава  с ориентацией (210) и со следующими физическими параметрами: толщина пленки h @ 13 mm, угол наклона оси легкого намагничивания θ @ 30º, намагниченность насыщения 4πMs @ 60 Gs, поле ромбической анизотропии Нк @ 1400 Oe. Был произведен теоретический расчет этой структуры для пленки с перпендикулярной анизотропией, что дало хорошее согласие теории с экспериментом.

 В настоящей работе предложена теория смешанной доменной структуры, состоящей из системы полосовых доменов и цилиндрического домена с наклонной намагниченностью, сделан расчет величины максимального изгиба доменной границы полосового домена. Учет наклона намагниченности позволил объяснить форму границы полосового домена в феррит-гранатовых пленках с ориентацией (210), обусловленную наличием наклонного цилиндрического магнитного домена.

Рассмотрим изолированный полосовой домен ширины w = 2a, расположенный вдоль координатной оси x в бесконечной пленке толщины h, при наличии внутри него наклонного цилиндрического магнитного домена радиуса R. Координатная ось z направлена перпендикулярно плоскости пленки, а ось y перпендикулярно доменной стенке. Начало системы координат помещено в центр цилиндрического домена. Магнитостатическое поле рассеяния цилиндрического домена искажает форму полосового домена и приведет к зависимости его ширины от координаты x. Пусть функция  описывает изгиб доменной стенки полосового домена (Рис. 1).

Тогда изменение магнитостатической энергии будет иметь вид функционала, зависящего от неизвестной функции . Вычисляя вариационную производную функционала изменения магнитостатической энергии и приравнивая ее к нулю, получаем нелинейное функциональное интегральное уравнение для функции . Полученное уравнение не имеет точного аналитического решения. Решение его численными методами представляет сложную математическую проблему. Однако, линеаризация этого уравнения позволяет получить приближенное аналитическое решение для формы доменных границ:

 

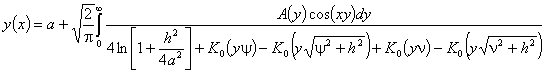,      (1)

где

 

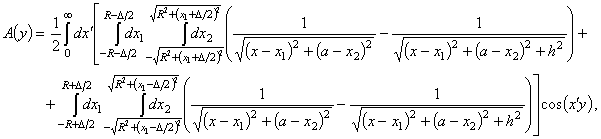
, , Δ — параметр наклона цилиндрического магнитного домена, b — максимальное значение функции , описывающей форму искажения доменной границы полосового домена в результате воздействия магнитостатического поля рассеяния наклонного цилиндрического домена.

Теоретический расчет величины максимального изгиба доменной границы полосового домена по формуле (1) при параметрах, соответствующих экспериментальным данным (w = 16 μm — ширина полосового домена, h = 13 μm — толщина магнитной пленки, R = 6,75 μm — средний радиус цилиндрического магнитного домена, Δ = 7,51 μm — расстояние между проекциями центров окружностей ЦМД на поверхность пленки), дает значение 3,6 μm. Максимальное значение величины изгиба доменной границы полосового домена, полученное в эксперименте для этих параметров, составило 3,9 μm.

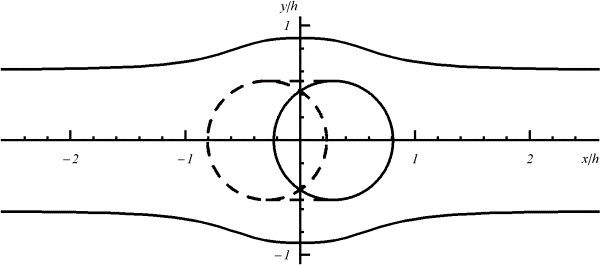
Рис.1.

Форма полосовой доменной структуры при наличии наклонного цилиндрического магнитного домена в магнитной пленке (на графике по осям x и y отложены безразмерные величины x/h и y/h).

 

Величина расхождения между экспериментальными результатами и теоретическими выводами для величины максимального изгиба границы полосового домена, получаемая при анализе формул (1) и рисунка 1, составляет 8 %.

Таким образом, величина максимального изгиба границы полосового домена, вычисленная по предложенной формуле (1), находится в хорошем соответствии с полученной экспериментально величиной изгиба доменной границы полосового домена, обусловленной влиянием поля рассеяния наклонного цилиндрического домена.

 

 

Литература.

1. Л. Д. Ландау, Е. М. Лифшиц. Электродинамика сплошных сред. — М.: Наука, 1992.

2. С. В. Вонсовский. Магнетизм. — М.: Наука, 1971.

3. А. Эшенфельдер. Физика и техника цилиндрических магнитных доменов. — М.: Мир, 1983.

4. Акимов М. Л., Поляков П. А., Усманов Н. Н. // ЖЭТФ, 2002, т. 121, № 2, с. 347–353.

5. Акимов М. Л., Поляков П. А. // Вестник Московского университета. Сер. 3. Физика. Астрономия, 2004, № 2, с. 47-50.